
😋 문제 분석
문자열 S가 주어진다. 시작 시 커서는 가장 왼쪽에 위치하며
알파벳 순서대로 문자열을 입력해야 하는데,
커서를 움직이는 횟수를 최소화하여야 한다.
✅ 문제 풀이
풀이를 그림으로 꼭 남기고 싶은 문제라 글을 적게 되었다.
우선 문제 접근을 어떻게 해야할 지 상식적으로 생각해보자.
baaab와 같은 문자열을 예시로 들어보겠다.
첫 커서는 인덱스 0에 위치하고 있고, 우리는 a 부터 입력해야 한다.
a를 다 입력한 뒤에는 b를 입력해야 한다.
우선 a를 다 입력하는 것부터 고민해보자.
현재 커서 위치가 0에 있으므로
가까운 인덱스 1의 a부터 인덱스 3의 a까지 오른쪽으로 쭉 진행하는 것이 합리적으로 보인다.
이제 인덱스 4의 b를 방문하고 인덱스 0의 b를 방문하면 최소 거리를 얻을 수 있다.
위 예시를 보면 현재 위치에 제일 가까운 인덱스부터 방문하는 게 정해처럼 보인다.
정말 그럴까? abaabc 예시를 보자.
인덱스 0의 a부터 인덱스 3의 a까지 쭉 진행한다.
여기서 가장 가까운 b는 인덱스 4의 b다.
인덱스 1의 b를 방문하는 것과 인덱스 4의 b를 방문하는 것을 비교해보자.
계산해보면 인덱스 1의 b를 방문하는 게 가까운 인덱스 4의 b를 방문하는 것보다 더 짧은 거리를 도출해낸다.
즉, 가까운 인덱스부터 방문하는 것은 정해가 아니다.
그리고 어차피 대상으로 하는 알파벳은 모두 지나야 하기 때문에 가장 왼쪽이나 가장 오른쪽 중에 하나를 도착지로 삼아야 한다.
알파벳의 가장 왼쪽 위치와 가장 오른쪽 위치 두 곳 다 가보고 기록해두어야 한다.
그 과정을 그림으로 표현해보겠다. 예시는 acbbacdda 이다.
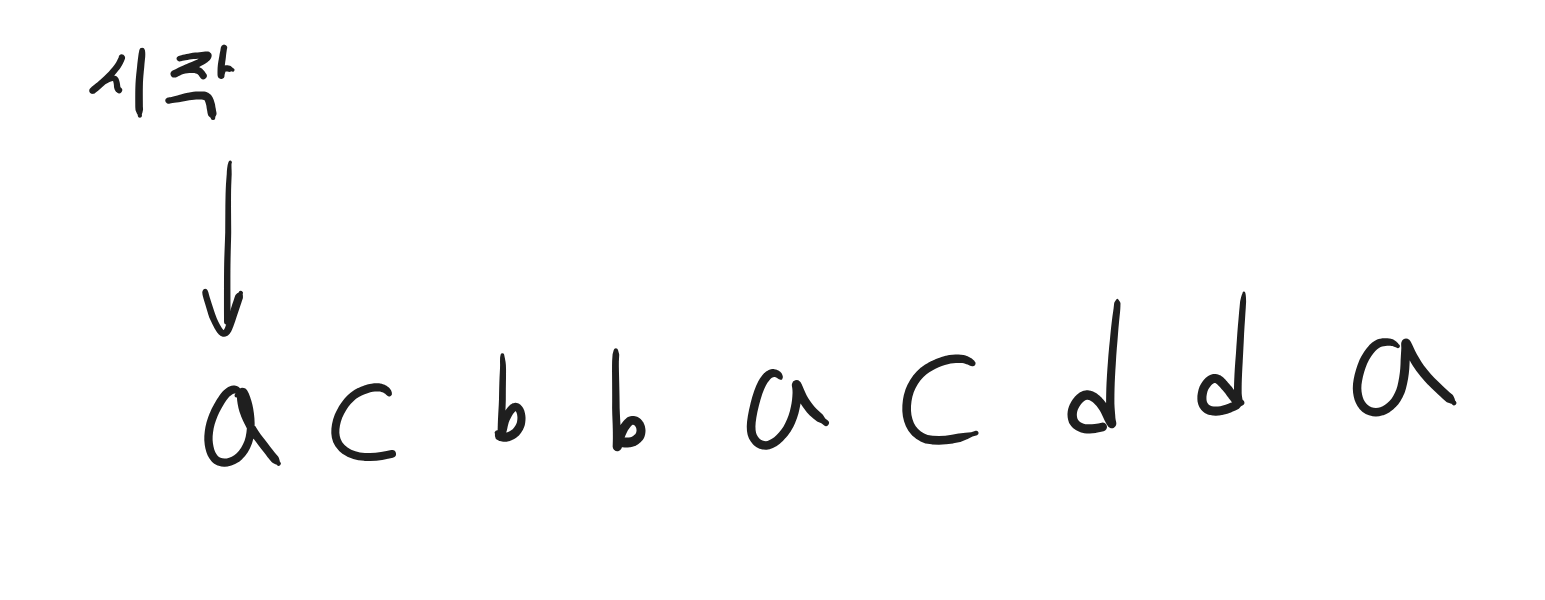
커서는 0 인덱스에 있다.

현재 입력해야 되는 알파벳은 문자열 S에서 사전 순으로 가장 앞서는 a이다.
제일 왼쪽 a ~ 제일 오른쪽 a 범위 내에 존재하는 a를 모두 입력해야 한다.
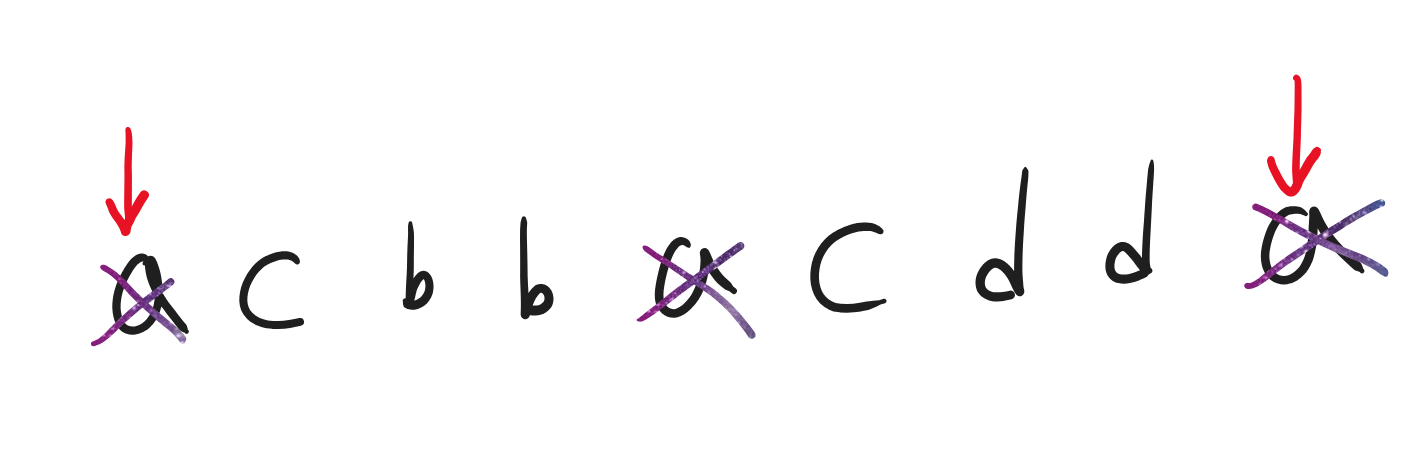
a를 모두 입력했다고 가정해보자.
그럼 가장 왼쪽 a에 커서가 위치하거나, 오른쪽 a에 위치하는 경우 두가지가 존재한다.
(b로 향하기 전에 어느 위치가 더 합리적일지는 아직 알 수 없다.)
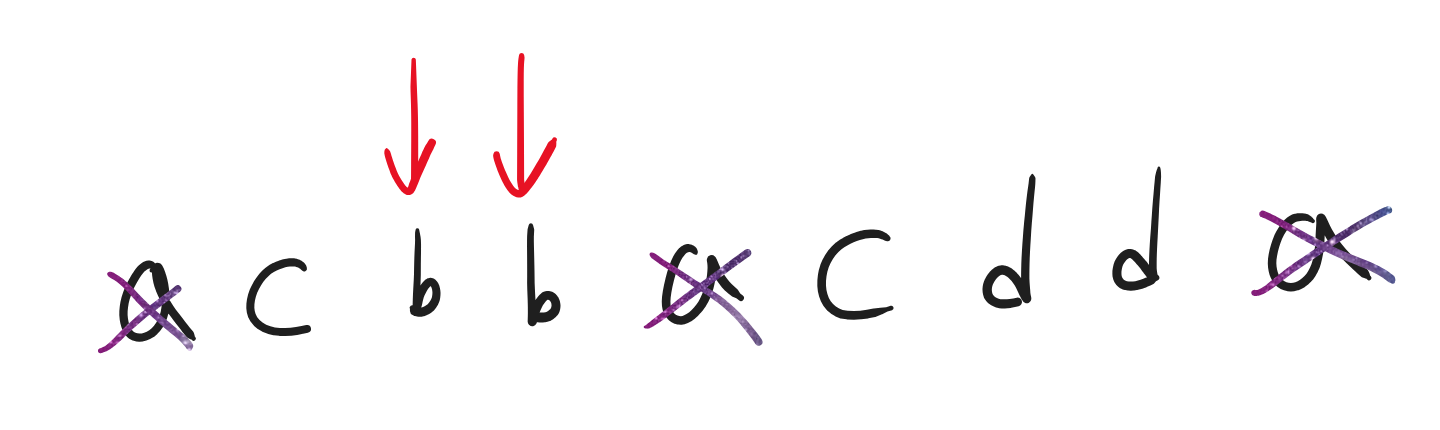
일단 제일 왼쪽 b와 제일 오른쪽 b는 아래와 같으며,
방금 전 두 경우의 수에서 도착할 수 있는 후보 지점이다.
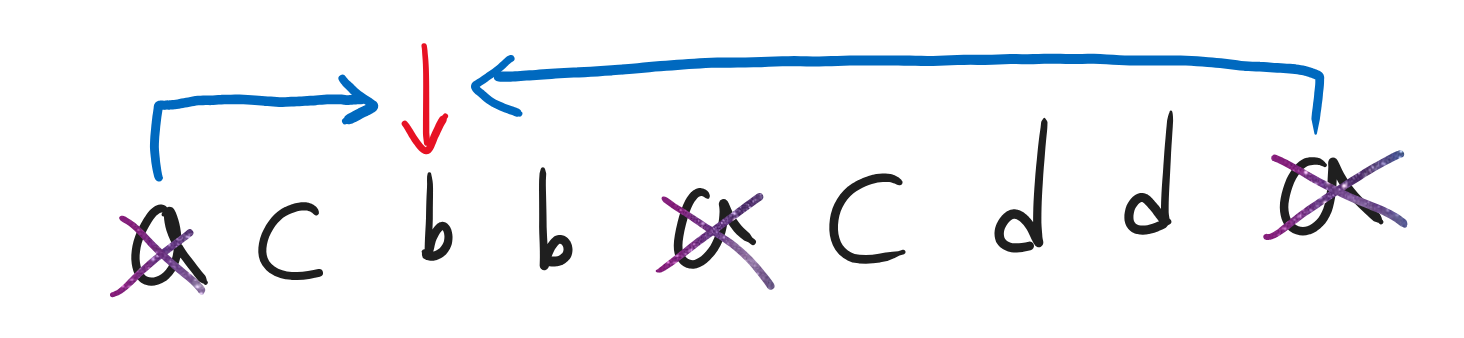
만약 제일 왼쪽 b를 도착지로 삼는다면, 아래와 같은 경우의 수가 가능할 것이다.
1. 가장 왼쪽 a에서 가장 왼쪽 b로 오기
2. 가장 오른쪽 a에서 가장 왼쪽 b로 오기
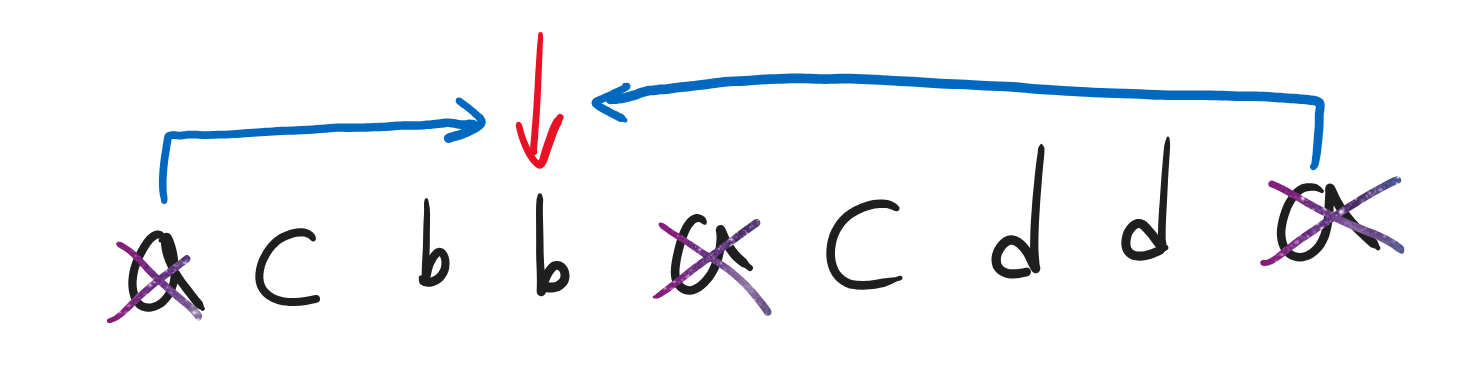
만약 제일 오른쪽 b를 도착지로 삼는다면, 아래와 같은 경우의 수가 가능할 것이다.
1. 가장 왼쪽 a에서 가장 오른쪽 b로 오기
2. 가장 오른쪽 a에서 가장 오른쪽 b로 오기
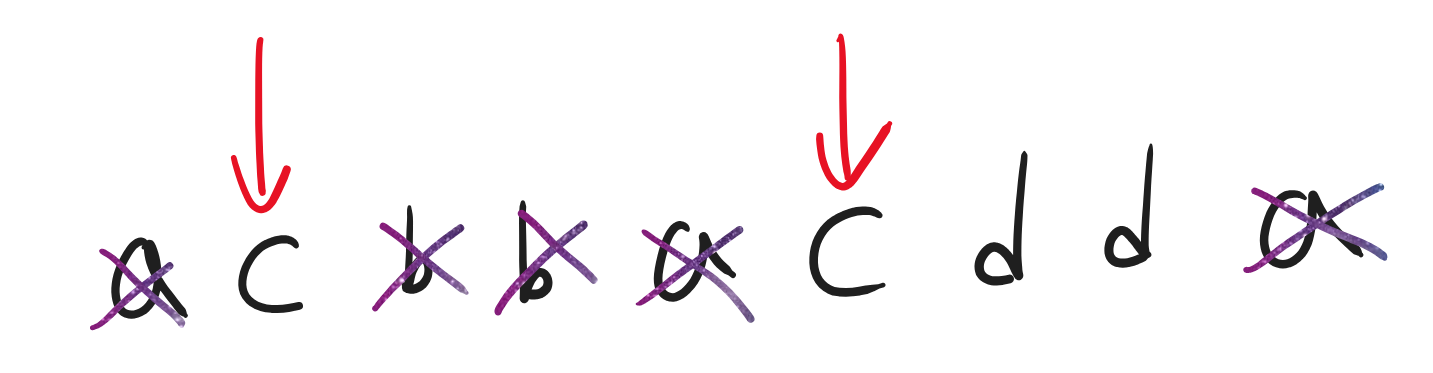
두 경우 다 기록했고 이제 c로 향해야 된다고 가정해보자.
제일 왼쪽 c와 제일 오른쪽 c가 똑같이 존재한다.
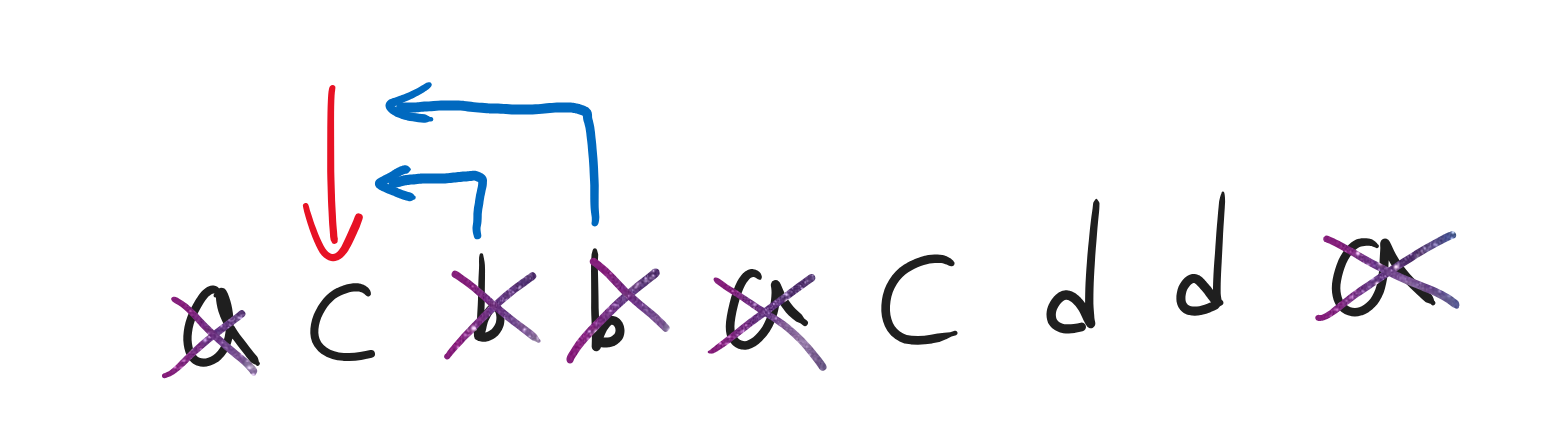
제일 왼쪽 c를 도착지로 삼는다면, 이번에도 아래와 같은 경우의 수가 가능하다.
1. 가장 왼쪽 b에서 가장 왼쪽 c로 오기
2. 가장 오른쪽 b에서 가장 왼쪽 c로 오기
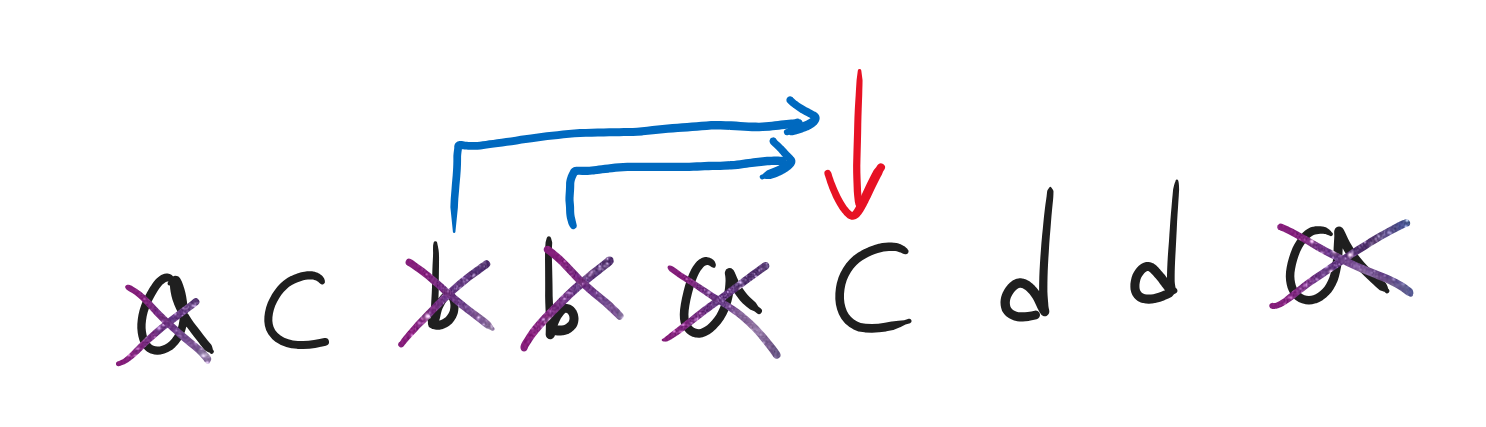
제일 오른쪽 c를 도착지로 삼는다면, 이번에도 아래와 같다.
1. 가장 왼쪽 b에서 가장 오른쪽 c로 오기
2. 가장 오른쪽 b에서 가장 오른쪽 c로 오기
위 로직에 따라 최소 거리가 계속해서 갱신된다.
마지막에는 기록된 두 경우의 수 중에 더 작은 값을 선택하면 된다.
코드로 확인해보자.
우선 문자열을 입력받고, 각 알파벳의 가장 왼쪽 인덱스 및 오른쪽 인덱스를 기록해둔다.
val S = readln()
val leftMap = mutableMapOf<Char, Int>()
val rightMap = mutableMapOf<Char, Int>()
for (i in S.indices) {
leftMap[S[i]] = minOf(i, leftMap.getOrDefault(S[i], Int.MAX_VALUE)) // 가장 왼쪽 인덱스
rightMap[S[i]] = maxOf(i, rightMap.getOrDefault(S[i], -1)) // 가장 오른쪽 인덱스
}이제 입력된 문자열을 알파벳 순으로 점검해나간다. leftMap 변수의 keys 속성을 활용하면 알파벳을 중복없이 얻을 수 있다.
val alphas = leftMap.keys.sorted()DP 테이블 변수도 선언할 것이다. 우선 첫번째 알파벳은 초기화해주자.
// dp[입력할 알파벳들의 인덱스][도착 위치(가장 왼쪽이냐 가장 오른쪽이냐)]
val dp = List(alphas.size) { IntArray(2) }.apply {
// 첫번째 알파벳 초기화
val (left, right) = leftMap[alphas.first()]!! to rightMap[alphas.first()]!!
val dist = right - left // 첫번째 알파벳의 가장 왼쪽부터 가장 오른쪽 사이의 거리
this[0][0] = right + dist // 원점 -> 가장 오른쪽 위치 -> 가장 왼쪽 위치(도착)
this[0][1] = left + dist // 원점 -> 가장 왼쪽 위치 -> 가장 오른쪽 위치(도착)
}이제 앞서 이해한 로직을 코드에 적용하자.
for (i in 1 until alphas.size) {
val (prevL, prevR) = leftMap[alphas[i - 1]]!! to rightMap[alphas[i - 1]]!! // 이전 알파벳의 최좌측 and 최우측 인덱스
val (l, r) = leftMap[alphas[i]]!! to rightMap[alphas[i]]!! // 현재 알파벳의 최좌측 and 최우측 인덱스
val dist = r - l // 현재 알파벳의 가장 왼쪽부터 가장 오른쪽 사이의 거리
// 1. 이전 알파벳 가장 왼쪽 위치까지 소모된 거리(dp[i - 1][0]) -> (이전 알파벳 가장 왼쪽 위치(prevL) ~ 현재 알파벳 가장 오른쪽 위치(r)) -> (가장 오른쪽 위치 ~ 가장 왼쪽 위치)(dist)
// 2. 이전 알파벳 가장 오른쪽 위치까지 소모된 거리(dp[i - 1][1]) -> (이전 알파벳 가장 오른쪽 위치(prevR) ~ 현재 알파벳 가장 오른쪽 위치(r)) -> (가장 오른쪽 위치 ~ 가장 왼쪽 위치)(dist)
dp[i][0] = minOf(dp[i - 1][0] + (r - prevL).absoluteValue, dp[i - 1][1] + (r - prevR).absoluteValue) + dist
// 1. 이전 알파벳 가장 왼쪽 위치까지 소모된 거리(dp[i - 1][0]) -> (이전 알파벳 가장 왼쪽 위치(prevL) ~ 현재 알파벳 가장 왼쪽 위치(l)) -> (가장 왼쪽 위치 ~ 가장 오른쪽 위치)(dist)
// 2. 이전 알파벳 가장 오른쪽 위치까지 소모된 거리(dp[i - 1][1]) -> (이전 알파벳 가장 오른쪽 위치(prevR) ~ 현재 알파벳 가장 왼쪽 위치(l)) -> (가장 왼쪽 위치 ~ 가장 오른쪽 위치)(dist)
dp[i][1] = minOf(dp[i - 1][0] + (l - prevL).absoluteValue, dp[i - 1][1] + (l - prevR).absoluteValue) + dist
}마지막 알파벳까지 기록된 두 값을 비교한 다음,
문자열 길이만큼 입력한 엔터를 더해주면 정답.
print(dp.last().minOf { it } + S.length)