백준 32754: 손이 닿는 범위

🧭 문제 분석

여러 개의 전자 기기가 좌표 평면에 위치하고 있으며, 코더빡의 위치는 원점이다.
원점에서 R만큼의 길이로 팔을 뻗을 수 있으며, 각 전자 기기는 무게 중심을 기준으로 회전이 가능하다.

✅ 문제 풀이

각 전자 기기는 무게 중심을 기준으로 회전이 가능하기 때문에,

원점까지 최대한 가까워 지도록 전자 기기를 회전 시키는 것이 유리하다.

사각형의 일부가 원점에 가장 가까워 지게 회전 시키려면 원점-꼭지점-무게중심을 통과하는 선분이 있도록 배치하면 된다.

사각형 입장에서 원점에 가장 길게 뻗을 수 있는 위치인 것이다.

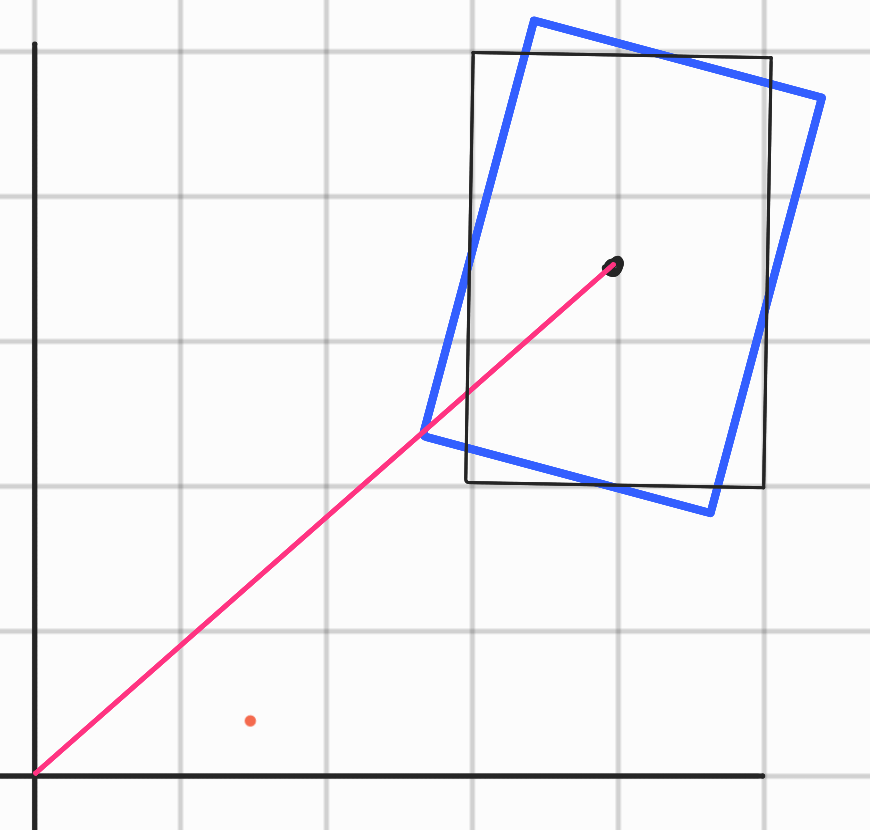
(파란색이 회전된 상태)

이 논리를 기준으로 무게 중심의 좌표를 구하고, 직사각형의 대각선 길이의 절반을 구한다.

사각형의 꼭지점은 시계 방향으로 제시되므로, 무게중심의 좌표는 쉽게 구할 수 있다.

val (N, R) = readln().split(" ").map(String::toInt)
val xys = List(N) {
    readln().split(" ").map(String::toDouble)
    .let { // it[0] = x1, it[1] = y1, it[2] = x2 ...
        // 첫번째 꼭지점과 세번째 꼭지점의 중심이 사각형의 무게중심이다.
        val mx = it[0] + (it[4] - it[0]).div(2)
        val my = it[1] + (it[5] - it[1]).div(2)
        ...
    }
}

이제 직사각형의 대각선 길이의 절반을 구하고 기록해둔다.

val (N, R) = readln().split(" ").map(String::toInt)
val xys = List(N) {
    readln().split(" ").map(String::toDouble)
    .let {
        ...
        // 루트 처리는 추후에 하기로 함
        val d = (x - it[0]).absoluteValue.run { this*this } + (y - it[1]).absoluteValue.run { this * this }
        Triple(x, y, d)
    }
}
...

앞서 언급했듯이 원점 - 무게중심 간의 거리에 대각선 길이 절반이 포함되는 경우가 사각형을 원점에 가장 가깝게 만드는 방법이다.

그래서 원점 - 무게중심 간의 거리에 대각선 길이의 절반을 차감했을 때 R 이하라면 팔에 닿는 거리라고 할 수 있다.

...
print(xys.count { (x, y, d) -> sqrt(x * x + y * y) - sqrt(d) <= R }