[ML][Model] 결정트리(Decision Trees)

• 분류, 회귀 모두 적용 가능한 지도 학습 모델(label 존재)
• 설명이 중요할 때 아주 유용한 모델
• 학습 방법 : 데이터를 분할해가는 algorithm으로 노드를 어떻게 분할하는가에 대한 문제를 학습한다.(if-else 방식)
  • leaf 노드가 순수해질 때까지 정보 이득이 최대가 되는 특성으로 데이터를 나누는 것을 반복한다.
  • 각각의 leaf(말단) 노드는 class의 label을 나타낸다.
  • 추론 시, leaf 노드로 분류된다.

• 장점

  • 결과를 해석하고 이해하기 쉽다.
  • whitebox model : 분류과정을 트리구조로 확인이 가능
  • 비선형, 비단조(non-monotonic), 특성상호작용 특징을 지니는 데이터에도 용이하게 적용될 수 있다.
  • 수치 자료, 범주 자료 모두에 적용 가능.
  • 자료를 가공할 필요가 거의 없음 : 특성상호작용(특성들끼리 서로 상호작용하는 경우)를 자동으로 걸러내고, 명제가 다소 손상되었더라도 잘 동작한다.
  • 학습 속도 : 합리적인 시간안에 대규모의 데이터셋을 분석할 수 있다.

• 단점

  • NP-완전 문제 : 항상 최적의 결정 트리를 찾는다고 보장할 수 없다. 결정 트리는 탐욕 알고리즘 같은 휴리스틱 기법을 기반으로 하고 있다.
    • 우선 선택된 변수에 따라 트리 모양과 구성이 매우 달라진다.
    • 부분 최적화에 의한 영향을 줄이기 위하여 이중 정보 거리(dual information distance, DID)와 같은 방법을 사용하기도 한다.(?)
  • 과적합 문제 : 제대로 일반화하지 못할 경우 너무 복잡한 결정 트리가 된다.
    • 가지치기 등의 방법을 사용하여 해결
  • 배타적 논리합, parity, multiplexer와 같은 문제를 결정트리로 학습하면 엄청 커진다.
    • 문제의 표현 방법을 바꾸거나 통계 관련 학습법, 귀납 논리 프로그래밍처럼 더 많은 표현을 할 수 있는 학습 알고리즘을 사용해야한다.
  • 데이터에 대한 결정경계가 직선이 아닐 경우 분류율이 떨어진다. 분할할 때 한 변수만 선택하기 때문이다.

• 과적합 주의 : 복잡한 트리는 과적합 가능성을 높인다.
  • 아래 파라미터 조절 및 유의미한 feature 확인
  • min_samples_split : 내부 노드에서 나눠지는 최소값
  • min_samples_leaf : 말단 노드에 최소한 존재해야 하는 샘플의 수를 설정
  • max_depth : 깊이를 제한. 가지치기(Pruning)
  • 특성중요도(feature importance) 확인

• 비용함수 : 지니불순도(Gini Impurity or Gini Index), 엔트로피(Entropy)

• 파라미터를 설정하지 않는다면 순환 분할(재귀적 반복)되어, 분할로 인해 새로운 예측값이 더이상 추가되지 않거나(분류) 부분 집합의 노드가 목표 변수와 같은 값을 지닐 때(회귀)까지 계속된다.
• 탐욕 알고리즘의 한 예시인 하향식 결정 트리 귀납법(top-down induction of decision trees , TDIDT)이다.

종류

결정 트리 학습법, wikipedia

• ML/AI 분야에서 개발, 발전 : 엔트로피, 정보이득 개념으로 분리기준을 결정

  • ID3 (Iterative Dichotomiser 3) :
  • C4.5 (successor of ID3) : ID3 알고리즘을 보완
  • C5.0 (successor of ID4) : C4.5를 보완

• 통계학 분야에서 개발 : 카이스퀘어, T검정, F검정 등의 통계분석법을 사용하여 분리기준을 결정

  • CART (Classification And Regression Tree)
  • CHAID (CHi-squared Automatic Interaction Detector) : 이 알고리즘은 분류 트리를 계산할 때 다단계 분할을 수행한다.

• MARS (Multivariate adaptive regression splines) : 더 많은 수치 데이터를 처리하기 위해 결정 트리를 사용한다.

• 조건부 추론 트리 (Conditional Inference Trees) : 과적합을 피하기 위해 여러 테스트에 대해 보정 분할 기준으로 비 - 파라미터 테스트를 사용하는 통계 기반의 방법이다. 이 방법은 편견 예측 선택 결과와 가지 치기가 필요하지 않다.

앙상블방법을 적용한 결정 트리
1. 랜덤 포레스트에서는 분류 속도를 향상시키기 위해서 결정 트리들을 사용
2. 부스트 트리는 회귀 분석과 분류 문제에 사용
3. 회전 포레스트는 모든 결정 트리가 먼저 입력 트리 중 임의의 부분 집합에 대한 주성분 분석 (PCA)을 적용하여 훈련됨

코드

sklearn.tree.DecisionTreeClassifier

from sklearn.pipeline import make_pipeline
from sklearn.tree import DecisionTreeClassifier
pipe = make_pipeline(
    OneHotEncoder(use_cat_names=True),  
    SimpleImputer(), 
    DecisionTreeClassifier(random_state=1, criterion='entropy')
)
pipe.fit(X_train, y_train)
print('훈련 정확도: ', pipe.score(X_train, y_train))
print('검증 정확도: ', pipe.score(X_val, y_val))
y_val.value_counts(normalize=True)		# 과적합인지 확인

결정트리 그리기

from sklearn import tree
model_dt = pipe.named_steps['decisiontreeclassifier']
tree.plot_tree(model_dt)
plt.show()

혹은 더 나은 그림인 graphviz 사용

# graphviz 설치방법: conda install -c conda-forge python-graphviz
import graphviz
from sklearn.tree import export_graphviz
enc = pipe.named_steps['onehotencoder']
encoded_columns = enc.transform(X_val).columns

dot_data = export_graphviz(model_dt, max_depth=3, feature_names=encoded_columns, class_names=['no', 'yes'], filled=True, proportion=True)

display(graphviz.Source(dot_data))

특성중요도 확인

importances = pd.Series(model_dt.feature_importances_, encoded_columns)	# DecisionTreeClassifier에 있는 변수 feature_importances_
plt.figure(figsize=(10,30))
importances.sort_values().plot.barh();

통계학과 데이터 마이닝, 기계 학습에서 사용하는 예측 모델링 방법 중 하나

비용함수

정보 이득(Information Gain), 엔트로피(Entropy)

정보 이득 : 정보가 가장 풍부한 특성으로 노드를 나누기 위해 최적화할 목적 함수를 정의하는데, 이 목적 함수는 정보 이득을 최대화하는 방향으로 분할한다.
특정한 특성을 사용해 분할했을 때 엔트로피의 감소량

정보 이득
이전 상태에서 주어진 정보를 갖는 상태로 바뀔 때 엔트로피 H의 변화
IG : 지니불순도, H : 엔트로피(Entropy)일 때
IG(T, a) = H(T) - H(T|a) = 분할전 노드 불순도 - 분할 후 자식노드 들의 불순도

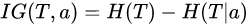
엔트로피
여기서 f는 node이고, fi는 특정 노드 f에서 클래스 i가 속한 샘플 비율이다.

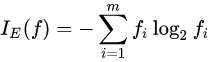
지니불순도(Gini Impurity or Gini Index)

집합에 이질적인 것이 얼마나 섞였는지를 측정하는 지표로 잘못 분류될 확률을 최소화하기 위한 기준이다.
CART(Classification And Regression Tree) 알고리즘에서 사용
집합에 있는 항목이 모두 같다면 지니 불순도는 최솟값(0)을 갖게 되며 이 집합은 완전히 순수하다는 의미이다.
반대로 클래스가 완벽하게 섞여있을 때, (50%, 50%)일 때 최대가 된다.

여기서 f는 node이고, fi는 특정 노드 f에서 클래스 i가 속한 샘플 비율이다.

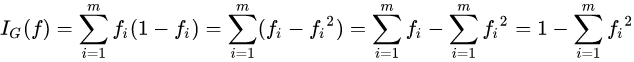
예시
A, B 두 class가 혼합된 data가 있을 때 (A, B) 비율로 지니불순도를 이해해보자.

• (45%, 55%)인 샘플은 불순도가 높다.
• (80%, 20%)인 샘플은 상대적으로 불순도가 낮고 순수도는 높다.
• (50%, 50%)인 샘플은 불순도가 최대가 된다. 이진분류의 경우 지니불순도는 0.5이다.
• (0%, 100%)인 샘플은 지니불순도가 최소인 0이 된다.
• 지니불순도나 엔트로피는 불순도와 비례한다.

---

참고

sklearn.tree.DecisionTreeClassifier
결정 트리 학습법, wikipedia
정보 이득, wikipedia
[머신러닝 교과서 with 파이썬 사이킷런 텐서플로 개정 3판], 세바스찬 라시카, 바히드 미자리리, 길벗