[정렬] 병합정렬(Merge Sort)

📌 병합 정렬(Merge Sort)

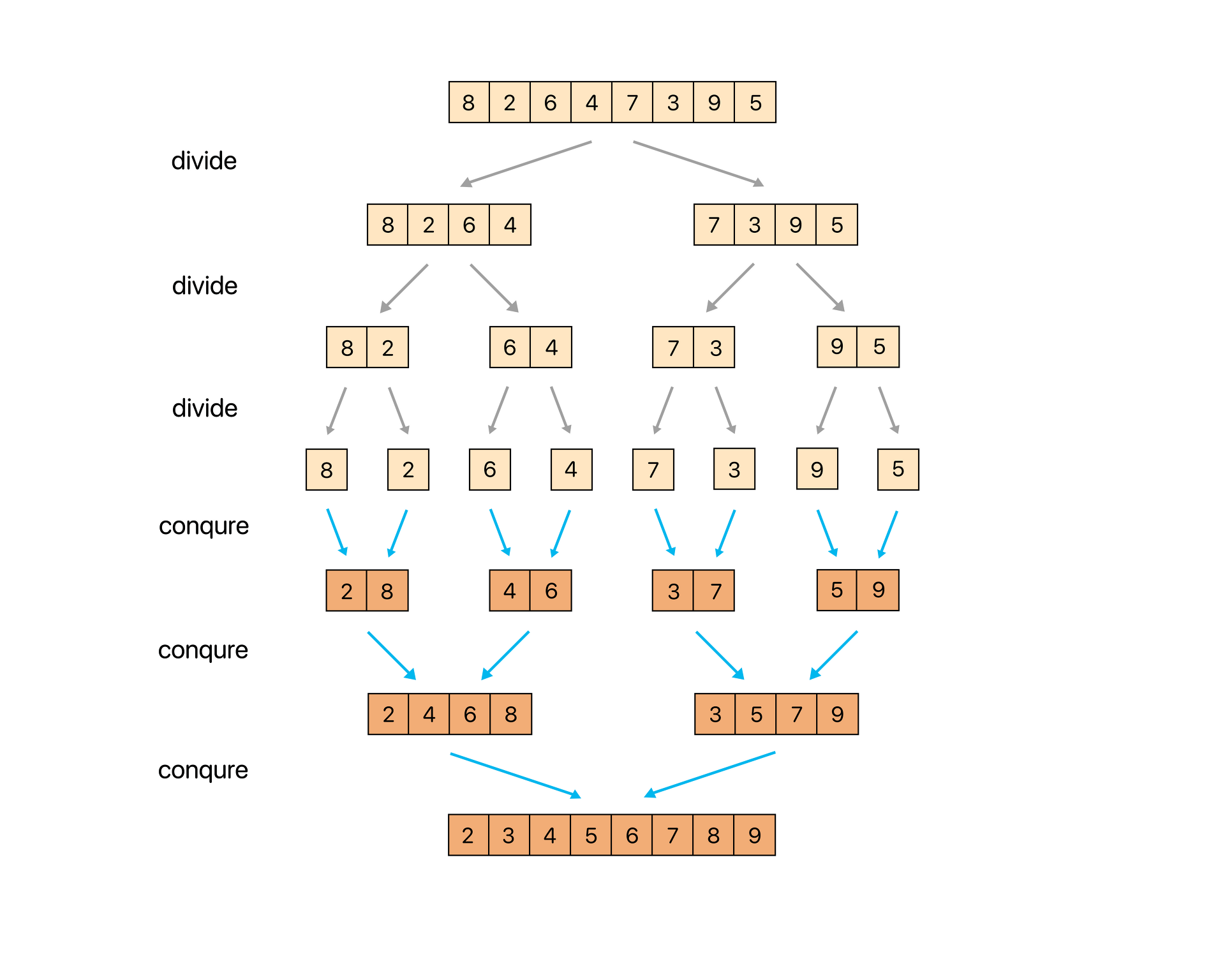
⭐ 개념

• 합병정렬이라고도 함
• 분할과 정복(Divide & Conquer)
• Top Down 방식

✅ 시간복잡도

• O(nlogn)

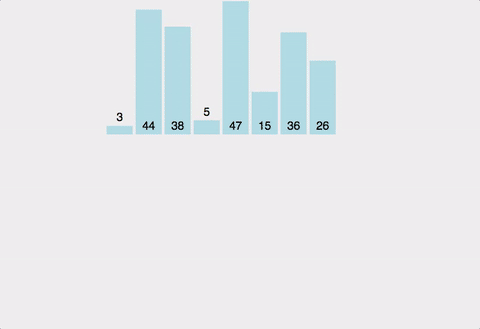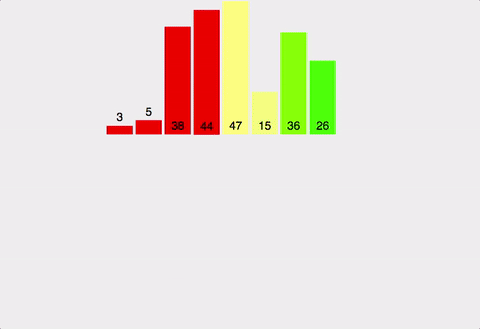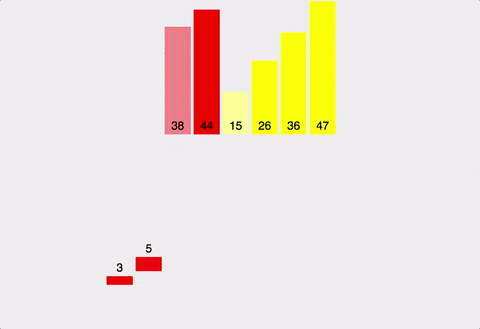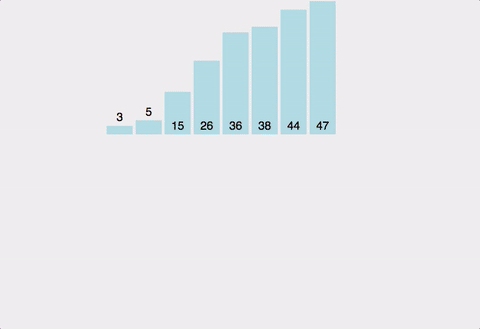
✅ 분할과 정복

• 큰 문제를 작은 문제 단위로 쪼개면서 해결해나가는 방식

✅ 퀵 정렬과의 차이점

• 퀵정렬 : 우선 피벗을 통해 정렬(partition) → 영역을 쪼갬(quickSort)
• 합병정렬 : 영역을 쪼갤 수 있을 만큼 쪼갬(mergeSort) → 정렬(merge)

⭐ 코드

static int[] sorted;
	
public static void main(String[] args){
	int[] arr = {67, 29, 34, 20, 11, 70, 53};
	
	sorted = new int[arr.length];
	merge_sort(arr, 0, arr.length-1);
}
	
// 범위를 나누는 과정
public static void merge_sort(int[] arr, int left, int right) {
	if(left == right) return;
	
	int mid = (left + right) / 2;

	merge_sort(arr, left, mid);	
	merge_sort(arr, mid + 1, right);
	
	merge(arr, left, mid, right);
}
	
// sorted 배열에 왼쪽오른쪽 배열비교해서 값 저장하는 단계
public static void merge(int[] arr, int left, int mid, int right) {
	int l = left;		// 왼쪽 부분리스트 시작점
	int r = mid + 1;	// 오른쪽 부분리스트의 시작점 
	int idx = left;		// 채워넣을 배열의 인덱스
	
	// 양쪽 값 존재할때, 비교해서 값 채워넣기
	while(l <= mid && r <= right) {
		if(arr[l] <= arr[r]) {
			sorted[idx] = arr[l];
			idx++;
			l++;
		}
		else {
			sorted[idx] = arr[r];
			idx++;
			r++;
		}
	}
	
	// 한쪽이 다 채웠을경우 나머지 채워놓기 => 어차피 부분배열안에서는 정렬되있음
	if(l > mid) {
		while(r <= right) {
			sorted[idx] = arr[r];
			idx++;
			r++;
		}
	}
	else {
		while(l <= mid) {
			sorted[idx] = arr[l];
			idx++;
			l++;
		}
	}
	
	// 기존배열에 복사
	for(int i = left; i <= right; i++) {
		arr[i] = sorted[i];
	}
}