[행렬] 고유값(Eigenvalue)과 고유벡터(Eigenvector), 그리고 주성분 분석(PCA)

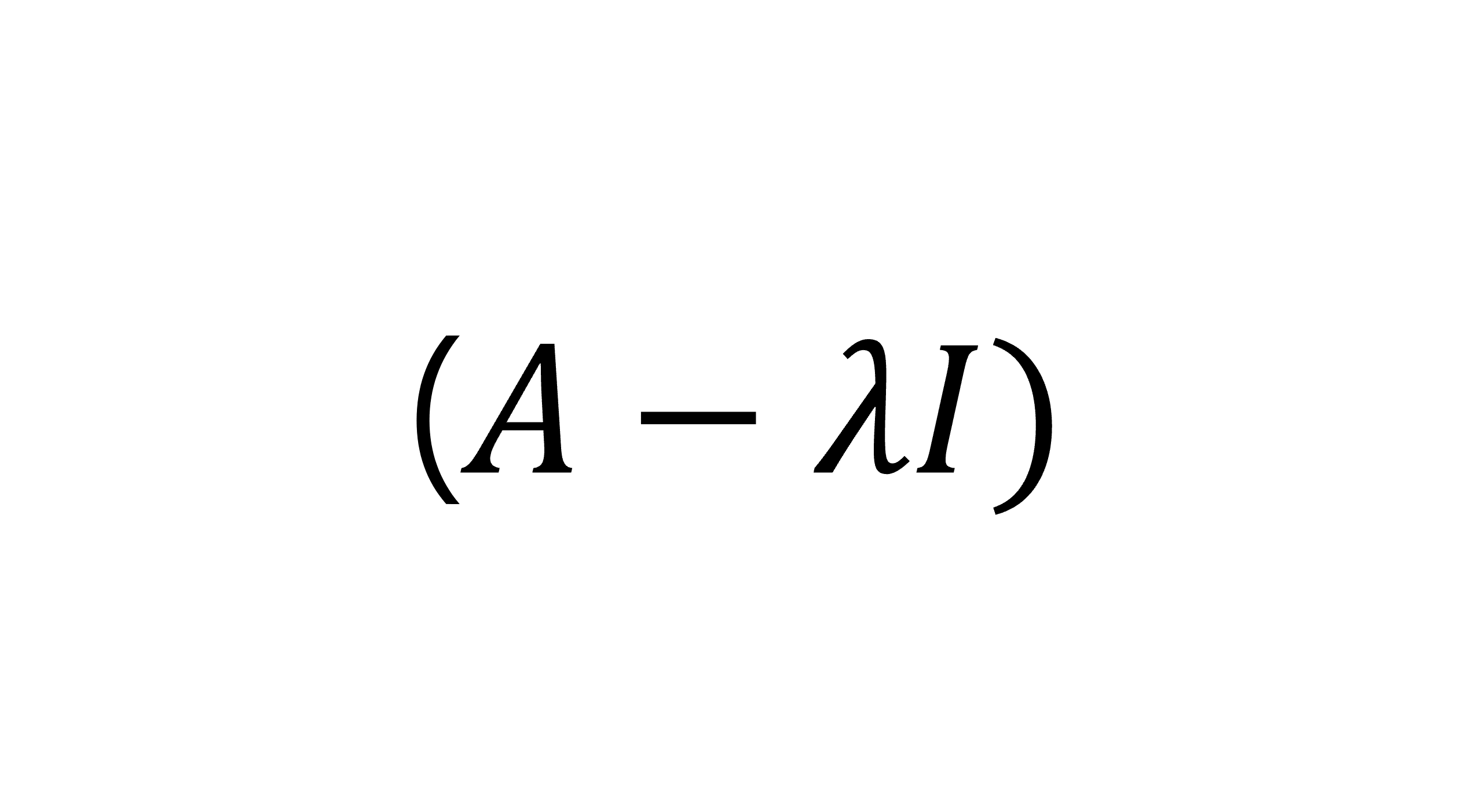
1. 행렬의 고유값(Eigenvalue)과 고유벡터(Eigenvector)

1-1. 고유값과 고유벡터의 개념 및 기하학적 의미

고유값(eigenvalue)과 고유벡터(eigenvector)는 행렬이 표현하는 선형 변환의 본질을 이해하는 데 핵심적인 역할을 하며, 다양한 응용 분야에서 활용된다.

선형 변환 : 벡터 공간에서 벡터를 다른 벡터로 변환하는 연산 예를 들어, 2차원 공간에서의 행렬

행렬 𝐴는 벡터 𝑥를 다른 벡터 𝐴𝑥로 변환한다. 이때 대부분의 벡터는 변환 과정에서 크기와 방향이 모두 변한다. 하지만 특정한 벡터는 이 변환을 거치더라도 방향은 그대로 유지되고 크기만 변화하는데, 이러한 벡터를 고유벡터라고 하며, 크기의 변화 비율을 나타내는 값을 고유값이라고 한다.

선형 변환은 다음과 같은 수식으로 표현할 수 있다.

$Av=λv$

𝐴 : $𝑛×𝑛$ 정방행렬
𝑣 : 고유벡터(Eigenvector) → 𝐴에 의해 변환되어도 방향이 변하지 않는 벡터
𝜆 : 고유값(Eigenvalue) → 고유벡터 𝑣의 크기 변화

양수의 고유값 𝜆 → 고유벡터의 크기는 변하지만 방향은 유지
음수의 고유값 𝜆 → 고유벡터의 크기는 변화하며 방향은 반대
고유값 𝜆 = 1 → 크기와 방향이 모두 변화 없다.
고유값 𝜆 = 0 → 고유벡터가 축소되어 사라진다.

이 개념은 선형 변환의 기하학적 특성을 이해하는 데 매우 중요하다.
고유벡터와 고유값은 벡터 공간의 구조를 분석하고, 변환의 고유한 특성을 파악하는 데 도움을 준다.

1-2. 고유값 방정식과 고유값의 계산

고유값과 고유벡터를 구하는 과정은 행렬의 고유값 방정식을 푸는 것과 같다.

$(A-λI)v=0$

$I$ : 단위행렬(identity matrix)
$λ$ : 고유값

이 방정식이 의미하는 바는, 행렬 $𝐴$에서 고유값 𝜆를 뺀 행렬 $A-λI$가 고유벡터 𝑣를 영벡터로 변환한다는 것이다. 이때, 고유벡터 𝑣가 자명하지(Trivial) 않은 해를 가지려면, 행렬 $A-λI$의 행렬식이 0이어야 한다.

$det(A-λI) = 0$

이 특성 방정식을 풀면 행렬 𝐴의 고유값 𝜆를 구할 수 있다. 각 고유값에 대해 대응하는 고유벡터는 행렬 $A-λI$의 영공간(null space)에 속하는 벡터이다.

1-3. 고유값 분해 (Eigen Decomposition)

고유값 분해(Eigen Decomposition) : 행렬을 고유값과 고유벡터로 분해하여 표현하는 방법

정방행렬 𝐴에 대해 𝑛개의 고유값 $λ_i$와 고유벡터 $𝑣_𝑖$가 존재하면, 𝐴를 다음과 같이 분해할 수 있다.

$A=VΛV^{−1}$

$V$ : 고유벡터로 구성된 행렬 ($V$의 각 열벡터는 행렬 $A$의 고유벡터)
$Λ$ : 대각행렬 (대각선 요소로 행렬 $A$의 고유값들이 위치)
$V^{−1}$ : $V$의 역행렬

이 고유값 분해는 행렬을 보다 간단하게 분석하거나 계산하는 데 유용하다.

• 행렬의 거듭제곱
• 행렬의 대각합(trace)

대칭행렬의 경우, 고유벡터들이 항상 서로 직교하므로 고유값 분해가 더 간단하다.
이때 $V$는 직교행렬(orthogonal matrix)이 되며, $𝑉^{−1} = 𝑉^𝑇$가 성립한다.

따라서 대칭행렬 $A$는 다음과 같이 분해할 수 있다.

$A=VΛV^{T}$

이와 같은 대칭행렬의 고유값 분해는 데이터 분석, 신호 처리, 기계 학습 등의 다양한 분야에서 활용된다.

2. 주성분 분석(PCA)

2-1. PCA

주성분 분석(PCA, Principal Component Analysis) : 고차원 데이터를 간단한 저차원 공간으로 변환하면서도, 원래 데이터의 손실을 최소화하는 차원 축소 기법이다. 데이터의 변동성(variance)을 가장 잘 설명하는 축을 찾아내고, 이 축을 따라 데이터를 투영(projection)하여 차원을 축소한다.

원 데이터가 위치한 공간에서, 데이터의 분산이 최대가 되는 새로운 좌표 축을 찾는다. 이 새로운 축은 데이터의 분산을 가장 잘 설명하는 방향이며, 첫 번째 주성분(Principal Component, PC1)이라고 불린다. PCA는 이 과정에서 상관성이 높은 변수들을 고려하여, 변수들 간의 상관성을 제거하고 데이터의 주요 패턴을 유지한다.

2-2. PCA의 수학적 원리

PCA의 수학적 원리는 고유값 분해(Eigen Decomposition)에 기반을 두고 있다.
이 과정에서 공분산 행렬의 고유값과 고유벡터를 계산하여, 고유값이 큰 순서대로 고유벡터를 정렬하고, 이들을 새로운 좌표 축으로 사용한다.

데이터 중심화 (Mean Centering) :
원 데이터의 각 변수에서 평균을 빼서, 데이터가 원점을 중심으로 분포하도록 한다. 이를 데이터 중심화(mean centering)라고 하며, 데이터 행렬 𝑋를 중심화한 결과는 다음과 같이 나타낼 수 있다:

$X_{centered} = X - \bar{X}$

여기서 $\bar{X} = \mu$로 $X$의 평균을 의미한다.

공분산 행렬 계산 (Covariance Matrix) :
중심화된 데이터를 바탕으로 공분산 행렬 $Σ$를 계산한다. 공분산 행렬은 데이터의 분산과 변수 간의 상관성을 나타내는 행렬로, 다음과 같이 정의된다:

$Σ = {1\over n-1} \; X^T_{centered} \; X_{centered}$

여기서 n은 데이터 포인트의 수이다.

고유값과 고유벡터 계산 (Eigenvalues and Eigenvectors) :
공분산 행렬 $Σ$의 고유값과 고유벡터를 계산한다. 고유값은 새로운 축의 중요도를 나타내며, 고유벡터는 새로운 좌표 축의 방향을 나타낸다.

$Σe=λe$

여기서 $λ$는 고유값, $e$는 고유벡터이다.

주성분 선택 (Selection of Principal Components) :
고유값의 크기 순서대로 고유벡터를 정렬하고, 가장 큰 고유값에 대응하는 고유벡터를 첫 번째 주성분(PC1)으로 선택한다. 두 번째로 큰 고유값에 대응하는 고유벡터는 두 번째 주성분(PC2)으로 선택한다. 이 과정을 반복하여 원하는 수의 주성분을 선택할 수 있다.

데이터 투영 (Projection of Data) :
선택된 주성분 축에 데이터를 투영하여, 저차원 공간으로 변환한다. 투영된 데이터는 원래 데이터의 중요한 정보를 최대한 유지하면서, 차원이 축소된 형태로 나타납니다.

$Z=XW$

$X$ : $n×p$ 크기의 데이터 행렬
$W$ : $p×k$ 크기의 주성분 벡터로 구성된 행렬 ($k$는 선택한 주성분의 수)
$Z$ : $n×k$ 크기의 축소된 데이터 행렬로 $p$차원의 데이터가 $k$차원으로 축소된 형태

2-3. 정보 보존과 차원 축소

PCA는 기존 데이터의 정보를 최대한 보존하면서, 즉 차원 축소 과정에서 발생하는 정보의 손실을 최소화하며 데이터의 차원을 줄이는 것이다. 하지만 모든 주성분을 사용하지 않고 일부만 선택하면, 데이터의 변동성 중 일부는 손실될 수밖에 없다. 따라서 정보의 손실을 최소화하되 선택하는 주성분의 수를 최소화하기 위해서 적절한 주성분의 수를 결정해야한다.

주성분의 수를 결정하기 위해, 스크리 플롯(Scree Plot)이나 분산 설명 비율(PVE, Proportion of Variance Explained)을 사용할 수 있다.

스크리 플롯(Scree Plot) : 각 주성분에 대응하는 고유값의 크기를 시각화한 그래프

고유값의 크기가 급격히 줄어드는 지점인 엘보 포인트(Elbow Point)를 찾는 것이 일반적이다. 이 지점 이후의 주성분은 설명력이 낮으므로 제외할 수 있다.

분산 설명 비율(PVE, Proportion of Variance Explained) : 각 주성분이 데이터의 총 변동성에서 차지하는 비율

$PVE = {\lambda_j \over \sum_{i=1}^p \lambda_i }$

$\lambda_j$ : 선택된 주성분의 고유값
$\sum_{i=1}^p \lambda_i$ : 전체 고유값의 합

원하는 수준의 변동성을 설명할 수 있는 최소한의 주성분 개수를 선택할 수 있다.