문제

https://www.acmicpc.net/problem/10844

나의 코드 (답안 참조)

"""
1. 아이디어
핵심은 2차원 dp를 만들어 앞에 오는 숫자를 가지고 테이블을 구성하는 것?

2. 시간복잡도
O(10(N-2)) 정도?
"""

from sys import stdin
input = stdin.readline

n = int(input())
dp = [ [0] * 10 for _ in range(n+1) ] # dp[0]은 무시할 수 있게 n+1만큼 생성

# 1 자리수는 0을 제외하고(조건 : 0은 앞에 올 수 없음) 1로 초기화
for i in range(1, 9+1):
    dp[1][i] = 1

# dp[N 자리 수][N자리 숫자일 때 해당 Index 앞에 올 수 있는 일의 자리 수]
# 2 자리수부터 시작
for i in range(2, n+1): # n 자리 수
    for j in range(10): # index

        # 뒷자리가 0일 때는 앞에 1밖에 오지 못함
        if j == 0:
            dp[i][j] = dp[i-1][j+1]
        # 뒷자리가 9일 때는 앞에 8밖에 오지 못함
        elif j == 9:
            dp[i][j] = dp[i-1][j-1]
        # 뒷자리가 2~8일 때는 앞에 숫자가 2개씩 올 수 있음
        else:
            dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1]

print(sum(dp[n]) % 1000000000)

    

느낀점

뒤에 있는 숫자를 기준으로 앞에 올 수 있는 숫자의 경우의 수를 구할 것이다.
자리수마다 각각의 숫자 앞에 올 수 있는 경우의 수가 다르므로 2차원 DP 테이블을 만든다.

dp[N의 수][N 자리 숫자일 때 해당 숫자 앞에 올 수 있는 일의 자리 수]

간단히 n = 2 자리일 경우를 먼저 보자.

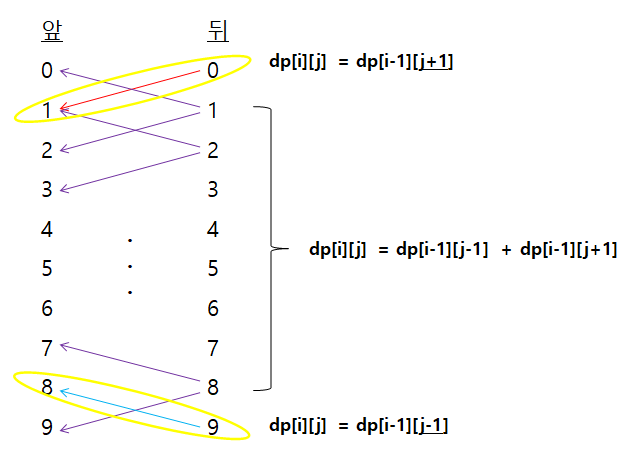
0 앞에 올 수 있는 숫자는 1 밖에 없고,
9 앞에 올 수 있는 숫자는 8 밖에 없지만
그 외에 2~8까지는 ±1한 숫자 2개가 올 수 있다.

그러므로 점화식을 작성하면

j가 0 일 때, dp[i][j] = dp[i-1][j+1]
j가 9 일 때, dp[i][j] = dp[i-1][j-1]
j가 2~8 일 때, dp[i][j] = dp[i-1][j-1] + dp[i-1][j+1]

이라고 할 수 있다.

이 때, 유의할 점은 1자리 수일 때 초기값은 1이지만 dp[1][0]은 0으로 초기화시켜주어야 한다.
0으로는 시작할 수 없다고 했으므로 '0'은 안된다.

이거 너무 어렵다.. 여러번 보자

참고자료

https://cijbest.tistory.com/19