문제

https://www.acmicpc.net/problem/12865

나의 코드 (답안 살짝참고)

"""
1. 아이디어
이전에 풀었던 퇴사 문제와 같이 역순으로 dp를 돌림으로써 최적해를 찾는다.

2. 시간복잡도
O(2nk)
"""

from sys import stdin
input = stdin.readline

n, k = map(int, input().split())
bags = [ list(map(int, input().split())) for _ in range(n) ]
dp = [0] * (k+1)
# dp[i] = 현재 무게제한이 i일때 최대 가치 누적

for w, v in bags:
    for i in range(k, w-1, -1):
        # max(현재 배낭의 가치 + 현재 배낭의 무게를 뺸 시점의 최대가치, 현재 무게재한이 i일떄 최대 가치)
        dp[i] = max( v + dp[i-w], dp[i] )

print(dp[-1])

    

느낀점

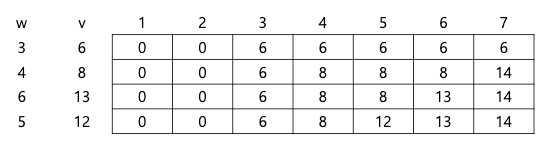
처음에는 쉬운 문제인줄 알고 그림을 작성하고 점화식을 찾은 다음 구현을 하고 제출했다.
테스트 케이스 까지 다 통과했기 때문에 맞았을줄 알았는데 틀렸길래 반례를 찾아보니 왜 틀렸는지 알게 되었다.

• 처음 생각한 그림
  
• 처음 제출한 코드

from sys import stdin
input = stdin.readline

n, k = map(int, input().split())
bags = [ list(map(int, input().split())) for _ in range(n) ]
dp = [0] * (k+1)

for w, v in bags:
    for i in range(w, k+1):
        dp[i] = max(v + dp[i-w], dp[i])

print(dp[-1])

반례
1 2
1 3
정답 : 3, 결과 : 6

근데 이때 두번째 반복문에서 w, k+1부분이 잘못 된것 같았다. 아무래도 직전에 동전1 문제를 풀어서 이 생각을 한 것 같은데 실수 했다.

그래서 최적해를 보장해주기 위해서 퇴사 문제와 같이 역순으로 dp를 해주었다.
역순으로 진행하면 최악의 경우부터 시작하기 때문에 최적해를 보장해줄 수 있다.
위의 반례 또한 통과된다.