[알고리즘] 시간복잡도

시간복잡도 (Time Complexity)

입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘이
효율적인 알고리즘이라 볼 수 있다.

Big-O는 상한 점근,
Big-Ω(omega)는 하한 점근,
Big-Θ(theta)는 그 둘의 평균을 나타낸다.

Big-O 표기법

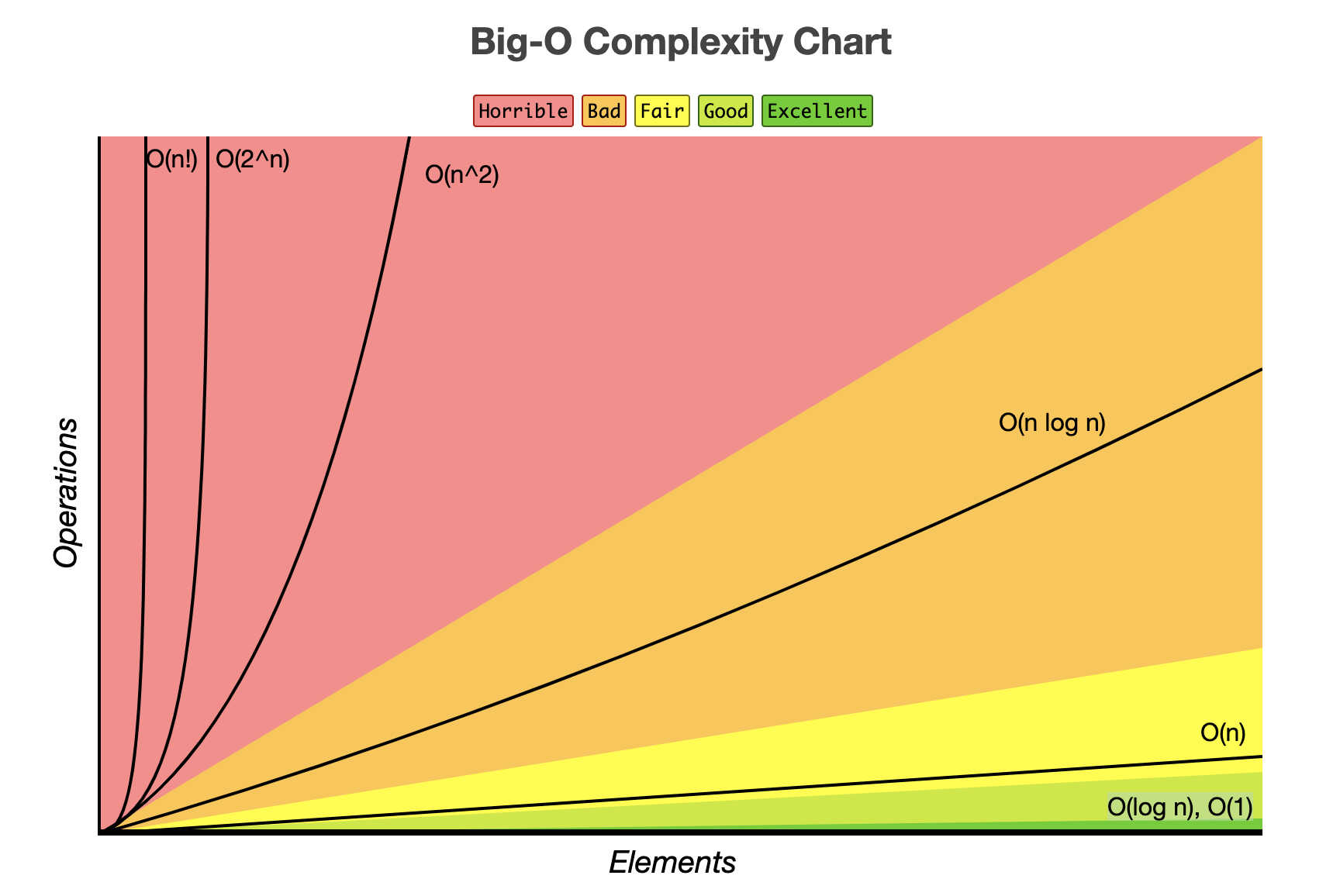
빅오 표기법은 프로그램이 실행되는 과정에서 소요되는 최악의 시간을 고려할 수 있다.

O(1)

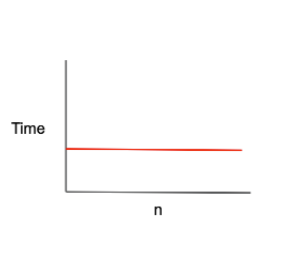
입력값의 크기와 상관없이 즉시 출력값을 얻을 수 있다.

예시

function O_1_algorithm(arr, index) {
	return arr[index];
}
let arr = [1, 2, 3, 4, 5];
let index = 1;
let result = O_1_algorithm(arr, index);
console.log(result); // 2

O(n)

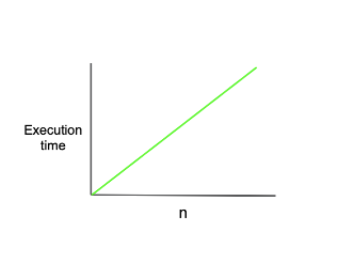
입력값이 증가함에 따라 시간이 비례적으로 증가한다.

예시

function O_n_algorithm(n) {
	for (let i = 0; i < n; i++) {
	// do something for 1 second
	}
}
function another_O_n_algorithm(n) {
	for (let i = 0; i < 2n; i++) {
	// do something for 1 second
	}
}

O(log n)

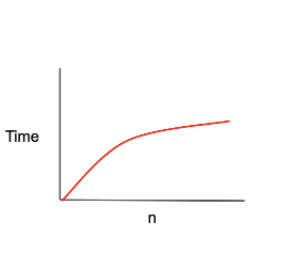
입력값이 증가할수록 시간이 줄어든다.

값을 탐색하거나 노드를 이동할 때마다 경우의 수가 절반으로 줄어드는
BST(Binary Search Tree)를 예시로 들 수 있다.

또 다른 예시

function O_log_n_arithm(n) {
  for (let i = 2; i <= n; i * 2){
    console.log(i)
  }
}

O(n^2)

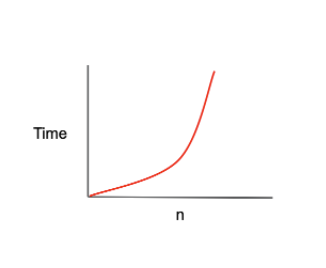
입력값이 증가함에 따라 시간이 제곱 비율로 증가한다.

예시

function O_quadratic_algorithm(n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
		// do something for 1 second
		}
	}
}
function another_O_quadratic_algorithm(n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
			for (let k = 0; k < n; k++) {
			// do something for 1 second
			}
		}
	}
}

O(2^n)

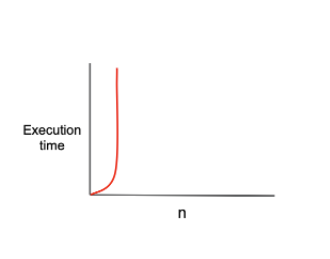
입력값이 증가함에 따라 시간이 2의 기하급수적으로 증가한다.
피보나치 수열이 대표적인 알고리즘이다.

예시

function fibonacci(n) {
	if (n <= 1) {
		return 1;
	}
	return fibonacci(n - 1) + fibonacci(n - 2);
}

입력값(N)에 따른 시간복잡도표

	O(N)	O(NlogN)	O(N^2)	O(2^N)
N=1	1	0	1	2
N=10	10	23	100	1024
N=100	100	460	10000	1267650600228229401496703205376