구름 - 이상한 미로(1차시기)

[문제 설명]

[문제 이해]

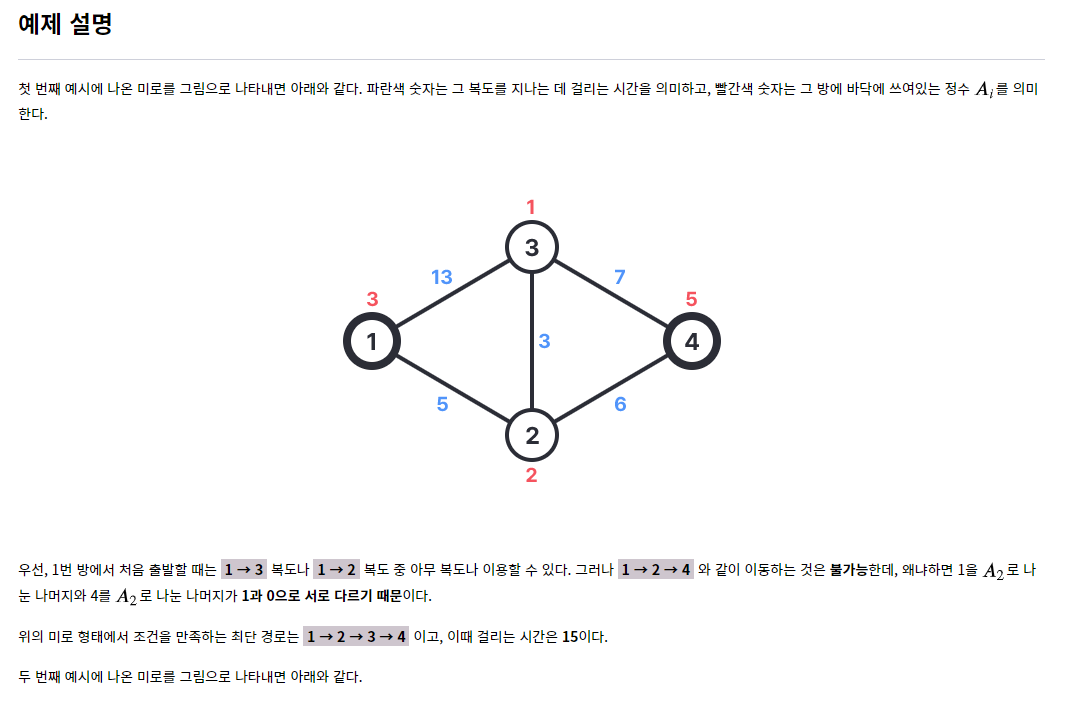
1~N개의 방이 주어졌을때 N번째 방까지 최소시간을 구하는 문제이다.
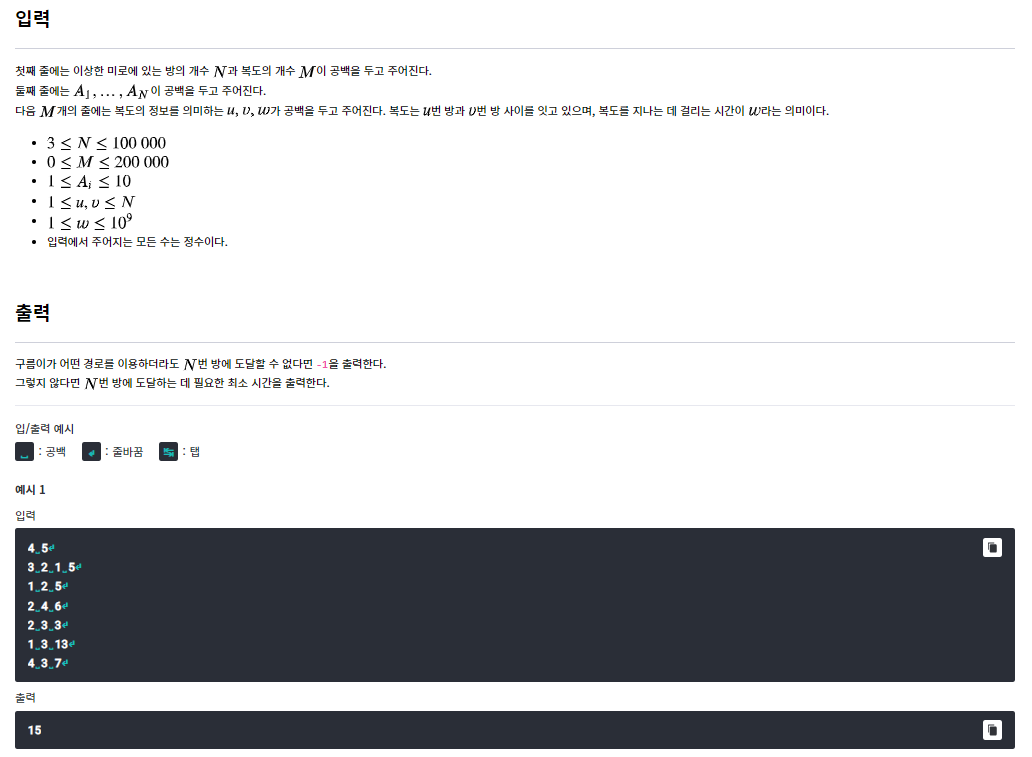
1.N의크기가 100,000 개 라는 정보를 확인하고 그래프에 대한 정보를 인접리스트로 작성해야된다고 생각했다.
ex) 1 : [2,5] 출발번호 : [도착지점: 거리]

2.그리고 최단시간이므로 bfs구현을 해야겠다고 생각을 했다.
하지만 일반 bfs와 달리 거리라는 가중치가 존재하므로 우선순위 큐를 사용해야겠다고 생각했다.
(이번글에서 구현 못함 ->필자가 생각나는 대로 구현하였다.)

[int[] 배열 정보]
i번째 지점과 관련 된 int[]형 정보를 출력하여 - 1번째 원소로 정렬
int[] 정보
[0]번째원소 : 도착지점
[1]번재원소 : 거리

3.반복문 안에 플래그가 존재한다.
flag 용도는 1번 지점에서 바로 연결되는 지점은 조건과 무관하게 바로 연결 될 수 있다.
그래서 처음 연결되는 지점은 바로 연결되고 flag를 true로 바꾼다.
다음 반복문에서는 3번째 지점부터 탐색하게 될것이므로 조건을 고려해야한다.

[조건 정보]
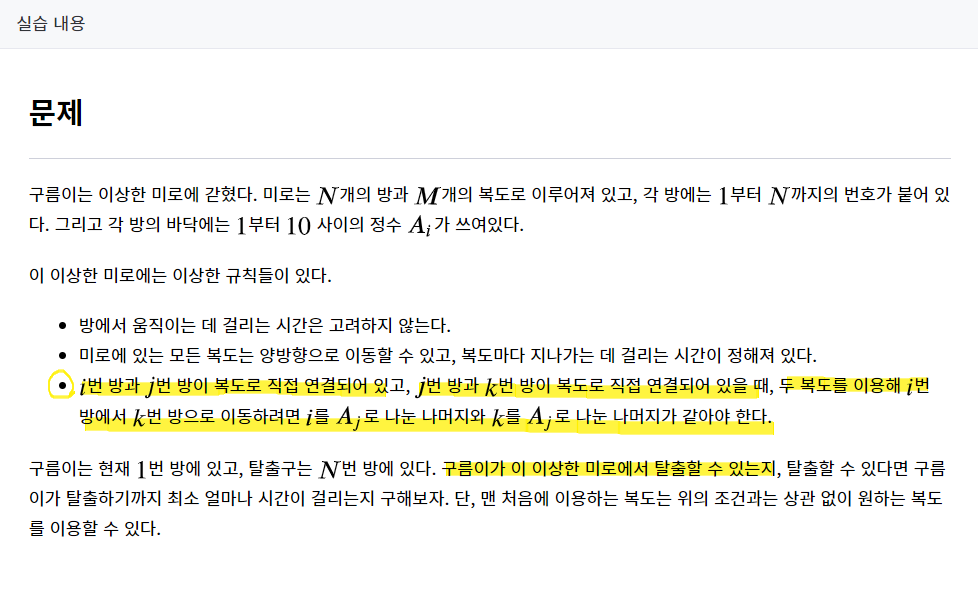
노란색 형광펜처럼 조건이 존재 했다.
i번째 방과 j번째 방이 연결되어 잇고, j가 k번째로 연결되어 있다면 3개의 복도를 연결하기 위해 
i%Aj[j] == k%Aj[j] 가 일치 해야한다라는 조건이 있다.

4. pre라는 이전 변수를 선언했다.
   조건을 적용하기 위해 curr(현재 노드) 와 pre(이전노드), target(다음 노드) 3가지 변수가 필요하다.

[조건] 노란색 형광펜처럼 조건이 존재 했다.
i번째 방과 j번째 방이 연결되어 잇고, j가 k번째로 연결되어 있다면 3개의 복도를 연결하기 위해
i%Aj[j] == k%Aj[j] 가 일치 해야한다라는 조건이 있다.

*여기서 Aj[i]는 방에 적혀잇는 번호(수)이다.

[소스 코드]

package Groom;

import java.io.BufferedReader;
import java.io.BufferedWriter;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.List;
class Adjancy1{
	 ArrayList<ArrayList<int[]>> list;
	
	 int n;
	
	public Adjancy1(int n){
		this.list = new ArrayList<ArrayList<int[]>>();
		
		for(int i = 0; i <n; i++){
			 this.list.add(new ArrayList<int[]>());
			
		}
		
		
		
		
	}
	
	// 연결 양방향
	public void addEdge(int start, int[] val){
		list.get(start).add(new int[]{val[0],val[1]});
	}
	
	// 리스트 하나를 가지고 오는 메서드
	public ArrayList<int[]> getList(int i){
		return this.list.get(i);
	}
	
	// 거리값만 가져오는 메서드
	public int getDist(int x,int y){
		ArrayList<int[]> list = this.list.get(x);
		// y 지점 찾기
		for(int i = 0; i<list.size(); i++){
			 int curr []= list.get(i);
			 if(curr[0] == y) {
				 return curr[1]; //거리 반환
			 }
		}
		return 0;
	}
	
	
	
}



public class 이상한미로 {
	public static void main(String[] args) throws Exception {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
		// 최단 경로를 찾는 문제
		// 조건이 존재
		// i->j->k로 이동시 
		// i%Aj == k%Aj가 같아야 이동할수 있다.
		// N의 크기가 100,000이다 => 인접 리스트로 구현해야 겠다.
		// w : 시간을 의미 10 ^ 9을 봐서는 long타입으로 반환
		

		String str[] = br.readLine().split(" ");
		int N = Integer.parseInt(str[0]);
		int M = Integer.parseInt(str[1]);
		String str1[] = br.readLine().split(" ");
		
		boolean visit[] = new boolean[N+1];
		int answer = 0; // 정답
		// Aj[]배열입력
		int Aj[] = new int[str1.length];
		for(int i = 0; i <str1.length; i++){ // 각 지점에 대한 표시값 Aj
			Aj[i] = Integer.parseInt(str1[i]);
		}
		Adjancy1 Adjancy1 = new Adjancy1(N+1); // 1-base
		for(int i = 0; i <M; i++){
			 		String str2[] = br.readLine().split(" ");
					int start = Integer.parseInt(str2[0]) ; // 출발지
					int end =  Integer.parseInt(str2[1]); //도착지
			    int dist = Integer.parseInt(str2[2]) ; // 사이 거리
			   //인접리스트 연결
			   Adjancy1.addEdge(start,new int[]{end,dist});
			   Adjancy1.addEdge(end,new int[]{start,dist});
			
						
		}
		// 구현
		// 1번 방부터 출발 , 도착방 : N
		LinkedList<Integer> q = new LinkedList<Integer>();
		
		q.add(1);
		visit[1] = true; // 출발지점 체크

		boolean flag = false;
		int pre = 0; // 이전 지점
		// bfs 구현 : 최당 연결
		while(!q.isEmpty()){
			 int curr = q.poll();
			 
			 if(curr == N) break; // 도착지점에 도착
			 
			 //  거리가 짧은 것순 
			 List<int[]> list = Adjancy1.getList(curr);
			 // 정렬
			 Collections.sort(list,new Comparator<int[]>(){
				 	public int compare(int [] a, int b[]){
						return a[1] - b[1];
					}
			 });
			if(!flag) {
				// 두번째 지점
				
					// 맞는 값이 있다면 => 연결이 된것
					// 조건 확인
					int targeting[] = list.get(0);
					int target = targeting[0];
					visit[target] = true;
					q.add(target);
					pre = curr;
					answer += Adjancy1.getDist(curr,target);// 지점 모든 연결값
					flag = true;
					
					
				
				
			}
			// 3번재 지점부터
			else {
				for(int i = 0; i <list.size(); i++){ // 연결 지점을 모두 순회
					// 맞는 값이 있다면 => 연결이 된것
					// 조건 확인
					int targeting[] = list.get(i);
					int target = targeting[0];
					
					if(!visit[target] && pre%Aj[curr-1] == target%Aj[curr-1]){ //조건에 맞은 성립
						visit[target] = true; //지점 연결 됨
						q.add(target);
						pre = curr;
						answer += Adjancy1.getDist(curr,target);// 지점 모든 연결값
						break;
					}
				}
				
			}
				
			}
		if(!visit[N]) { // 도착지점에 도달하지 못했다면
			answer = -1;
		}
		bw.write(answer+"\n");
		bw.flush();
		bw.close();
		br.close();
		
		
	}
}

결과 (20/47)

다음 포스팅에서는 이상한 미로2에 다시 작성하려고 한다.