[문제 설명]
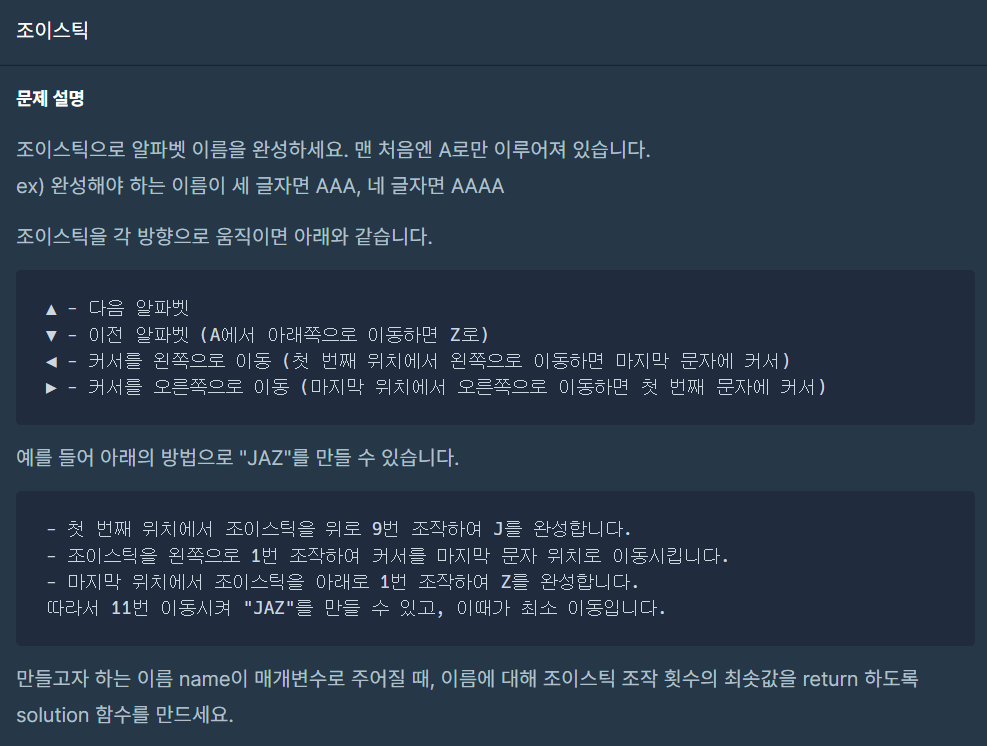
출처 : https://school.programmers.co.kr/learn/courses/30/lessons/42860
[문제 이해하기]
문제 에서 중요한점은
1.상,하 조건
한 지점을 변경하시 어떤 것이 유리할까?
A부터 올라가기 or Z부터 내려 오기
문제에서는 A <-> Z 로 1 움직임으로 변경이 가능하다고 표기 되어있다.
그래서 어떤 지점(target)이 있다고 하면
Math.min(target - A' , 'Z' - target + 1) 비용을 찾는다.2.좌,우 조건
이 부분이 많이 헷갈렷다
예를 들어
AAABBABAA라고 제시 되어있다.
일단 A지점은 사실 건들 필요가 없다(이미 A이기 때문에)
그래서 B지점들을 찾아 변경해야하는데 0번째 인덱스 부터 B지점들을 찾아 A로 변경할지 n-1 인덱스 부터 B지점들을 변경할지 생각해야한다.
예시처럼 AAA'B'BABAA ('' 지점 표기)
1.'B'지점까지 찾고 다시 앞으로 되돌아가 맨뒤로 다시 접근하여 해결할수도 있다.
나머지 B를 바꾸는 방법이 존재하고
2.처음부터 맨뒤부터 'B'지점으로 접근하며 B들을 변환하고 다시 맨뒤로 되돌아와 앞의 원소들을 처리하는 방법이있다.
3.그리고 그냥 0번째 부터 N-1까지 순차적으로 변경하는 방법 총 3가지가 존재한다.
그리고 이것은 각 인덱스별로 각각 위의 조건 3가지를 확인해야한다.
예를 들어
'A'AABBABAA 지점도 1,2,3 조건을 확인
A'A'ABBABAA 지점도 1,2,3 조건을 확인
AA'A'BBABAA 지점도 1,2,3 조건을 확인
:
AAA'B'BABAA 지점도 1,2,3 조건을 확인
각 지점마다 1,2,3조건을 확인하며 지점마다 연속되 A갯수를 찾는다.
연속된 A가 시작되는 지점이 start start을 늘려가며 이어서 계속찾는다(각 인덱스마다)
[전체 소스코드]
class Solution {
public int solution(String name) {
int answer = 0;
char names[] = name.toCharArray();
int n = names.length;
int move = n-1; // 순차적 접근
// 구현
for(int i = 0; i <n; i++){
// 좌우
// 세가지 경우를 살핀다.
// 1. 그냥 순차적으로 탐색하는 경우
// 2. 연속된 A구간에 맞춰 앞으로 되돌아가는 방법 i*2 + n - start
// 3. 연속된 A구간에 맞춰 뒤로 되돌아가는 방법 n-start * 2 + i
// 이중 최소값
// 각 원소마다 위의 3가지를 체크한다.
//[0] : //1,2,3 조건 체크
//[1] : // 1,2,3 조건 체크
//[2] : // 1,2,3 조건 체크
// 연속된 A지점 찾기
// 초과 범위생성
// i번째 지점의 +1 지점 부터 확인 := i+1이 'A' 인지 확인
int start = i + 1;
while(start < n && names[start] == 'A'){
start++;
}
move = Math.min(move,Math.min(i + (n -start) * 2, (i * 2) + n-start));
// 한지점 변경
answer += Math.min(names[i]-'A','Z'-names[i] + 1);
}
return answer + move;
}
}
