Housing Price Prediction Example with Neural Networks:
-
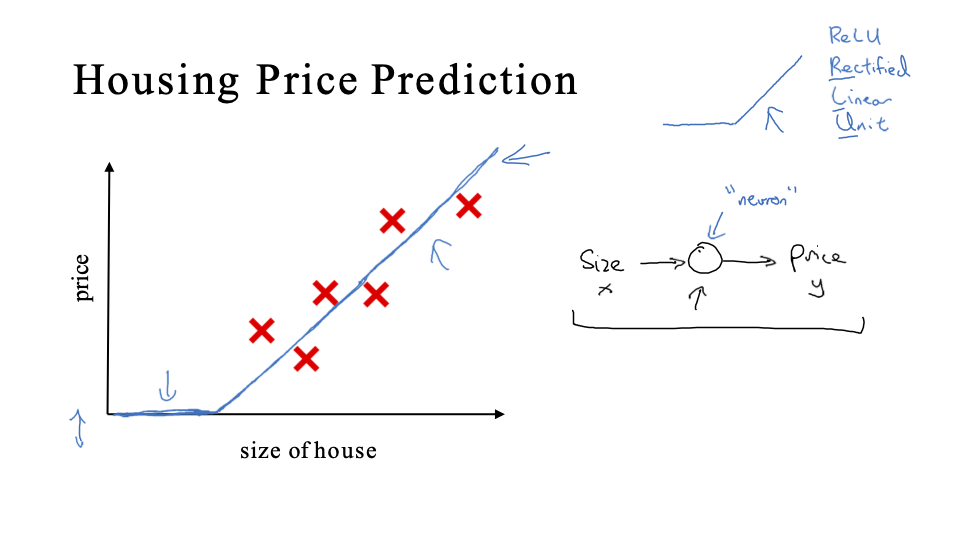
A simple model is described where house prices are predicted based on the size of the house.
-
Initially, a linear regression approach is suggested, but due to the realization that prices can't be negative, a ReLU (rectified linear unit) function is introduced.
-
This
ReLU functionensures the output price never goes below zero. -
This simple function can be visualized as the simplest neural network with a single neuron. The input is the size of the house (x) and the output is the estimated price (y).
-
The ReLU function takes an input size, computes a linear function, applies a max of zero, and then outputs an estimated price.
-
For a more complex model, multiple features such as the number of bedrooms, zip code (indicating walkability and school quality), and neighborhood wealth are used to predict house price.
-
By connecting multiple simple neurons, a larger neural network is formed. Each of these neurons can be thought of as a "Lego brick" contributing to the overall network.
-
In a neural network, intermediary calculations (like estimating family size, walkability, and school quality) are done by hidden units. Each of these units can access all input features, making them densely connected.
-
Given enough training data, neural networks excel at finding accurate mapping functions from input (x) to output (y).
-
Neural networks, especially in the described structure, are commonly applied in supervised learning scenarios.
The emphasis throughout is on the versatility and power of neural networks in handling complex relationships and multiple features in data, particularly for supervised learning tasks.
