CRLS 책을 근거하고, 출처, 출처2를 참고하여 작성하였습니다.
Red-Black Tree
BST (Binary-Search-Tree)의 한 종류로 트리의 균형을 위해 고안된 방법
- BST의 특징을 갖는다.
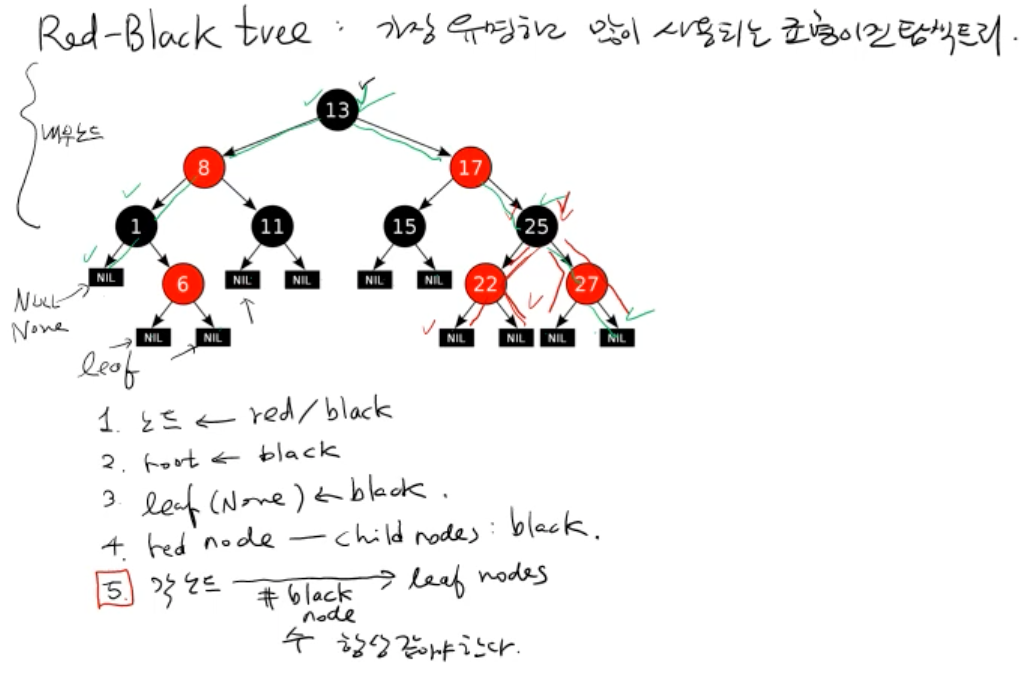
특징
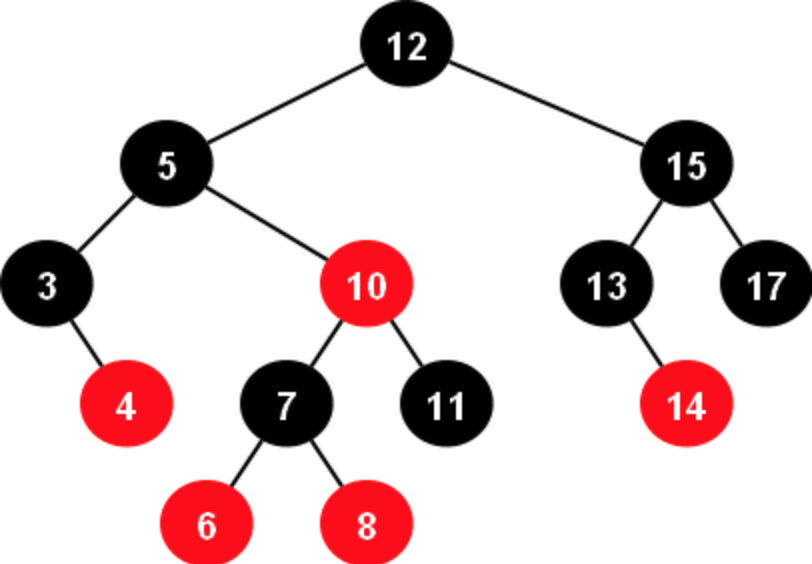
- 모든 노드는 레드/블랙 색상을 가진다.
- 루트는 블랙이다.
- 모든 리프(NIL = NULL, None)는 블랙이다.
- 레드 노드의 자식은 반드시 블랙이다.
- B-B (o), R-B (o), B-R-R (x)
- 블랙 노드의 개수는 높이의 절반보다 크거나 같다 bh >= h/2
- 각 노드에서 리프 노드로 가는 경로에서 블랙 노드의 개수는 항상 동일하다.
-> 위 조건에 의해 "RBtree는 균형잡혀있다" 하다
+ 여기서 리프 노드는 일반적인 의미의 리프 노드와 다르다. 모든 NIL 포인터가 NIL이라는 리프 노드를 가리킨다고 가정한다.
각각의 leaf 노드가 하나의 NIL을 가리키게 함으로 저장공간의 낭비를 줄일 수 있다.
O(logn) 증명
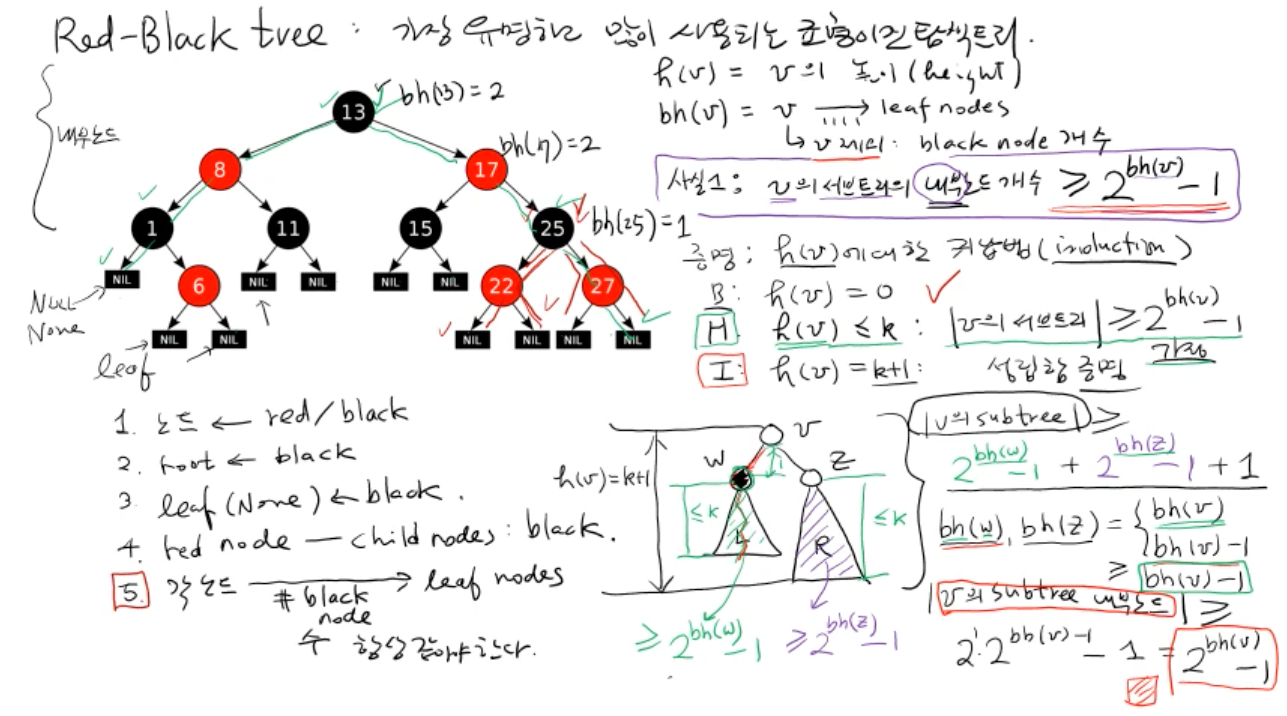
h(v) = 높이, bh(v) black-height = v부터 리프 노드까지의 블랙 노드 개수 (단, v는 제외)
부모 노드 v, 자식 노드 w, z
- |v의 내부노드의 개수| >= bh(v) - 1
- Base : h(0) = 0: 0 >= 2^0 - 1 = 0
- Hyphothesis : h(v) = k: |v의 내부노드| >= 2^bh(v) - 1
- Induction : h(v) = K + 1 일때,
|v의 내부노드| >= 2^bh(v) - 1
|w의 내부노드| >= 2^bh(w) - 1
|z의 내부노드| >= 2^bh(z) - 1
|v의 내부노드| >= |w의 내부노드| + |z의 내부노드| + 1(v 자기자신)
|v의 내부노드| >= (2^bh(w) - 1) + (2^bh(z) - 1) + 1
i) w = red, bh(w) = bh(v)
ii) w = black, bh(w) = bh(v) - 1
- 따라서 최솟값으로 하기 위해, Hyphothesis에 따라
- bh(w), bh(z) = bh(v) - 1
|v의 내부노드| >= 2 * 2^(bh(v) - 1) - 1
|v의 내부노드| >= 2^bh(v) - 1 성립
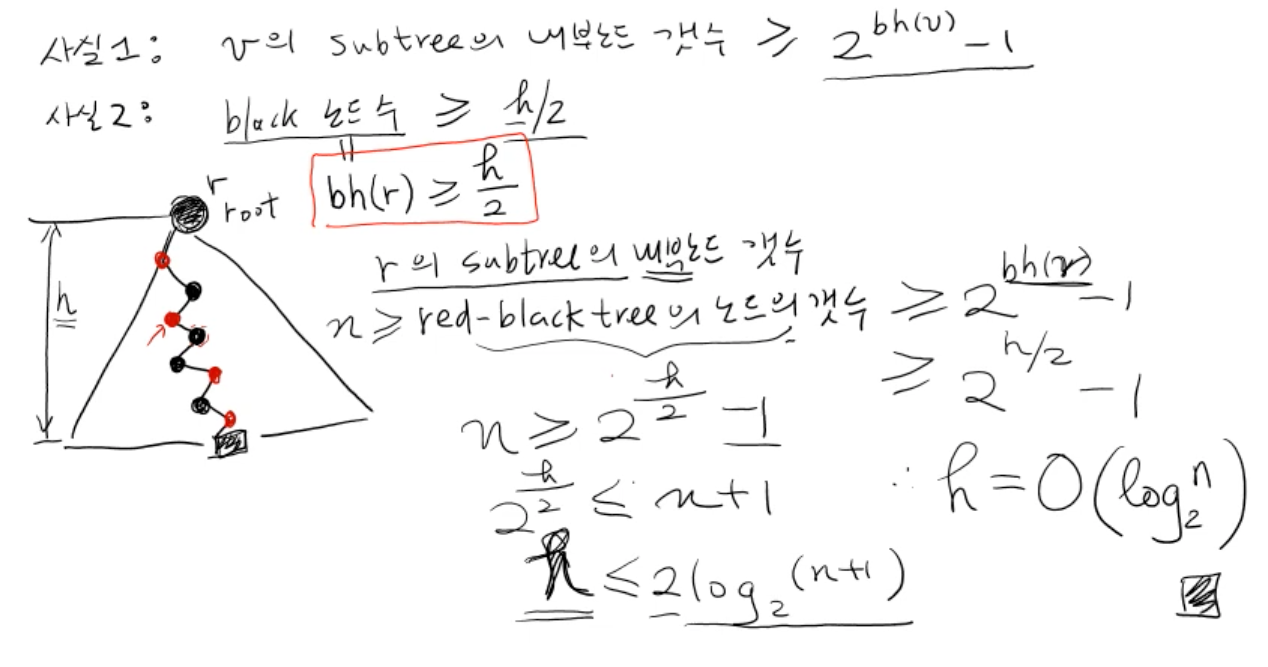
- bh(v) >= h/2 ; 블랙 노드의 수는 높이의 절반보다 크거나 같다
n은 트리의 노드의 개수, r은 root
n >= |r의 내부노드| >= 2^bh(r) - 1
n >= 2^(h/2) - 1
n + 1 >= 2^(h/2)
log (n + 1) >= h/2
2log (n + 1 >= h
높이 h는 최대 2log(n + 1) 만큼 가지고, 따라서 시간복잡도는 O(log n)이다 (검색, 삽입, 삭제)
검색
- 검색은 RBTree는 만들 때 밸런스를 맞춰서 만들기 때문에 BST와 동일하다.
- O(log n)
삽입
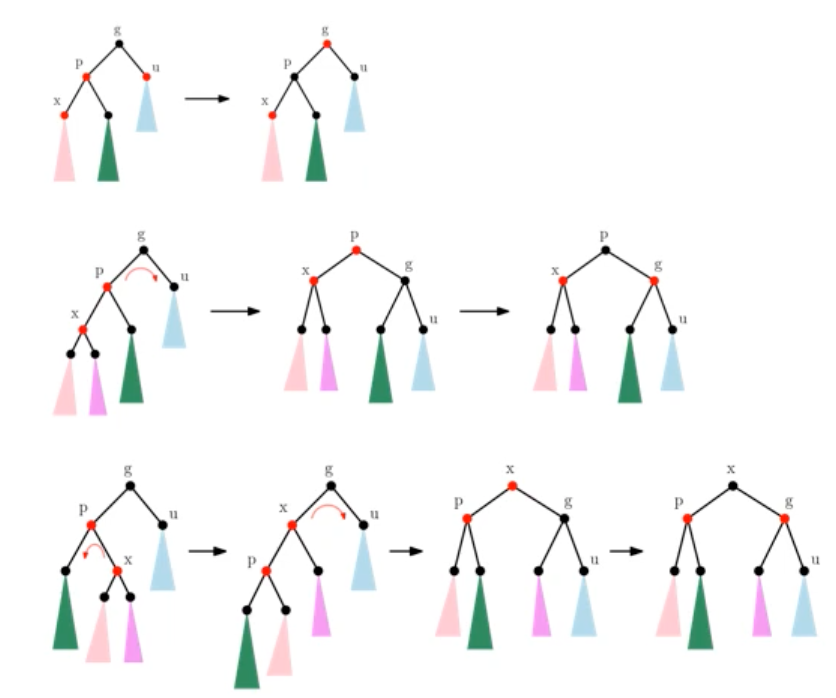
3-1, 3-2-a, 3-2-b 의 순서도
세 개의 주요한 단계
- 새 노드가 삽입되고 적색으로 칠해질 때 레드블랙 특성에 대해 어떤 위반사항이 발생되는가?
- 삽입 후 while문을 돌 때 어떤 점들을 고려하며 수행하는가?
- while문에서 나뉘는 세 가지 경우를 확인해야한다.
주의할 점
- 루트 노드는 흑색이다. (조건 2)
- 레드 노드 자식 노드는 무조건 블랙 노드 (조건 4)
- BST의 insert 연산을 호출해 새로운 노드(x)를 삽입
- 삽입된 노드 x는 무조건 red
- 왜 why?, 주의할 점 1, 2번에서 2번을 위반하는 경우가 더욱 복잡하기 때문에, 1번을 수정하는게 더욱 편하다.
- 4가지 경우로 나눠 조정
- x == t.root,
- x.color = black
- x.parent.color == black,
- do nothing
- x.parent.color == red,
- x.uncle.color == red,
- x.grandparent.color = red; x.parent.color, x.uncle.color = black
- g의 입장에서 black 노드의 개수는 동일하다. (!=black height), p, u의 입장에선 black 노드의 개수는 1 증가
- x.uncle.color == black,
- a. x, p, g = linear한 경우 - rotate, recolor
- b. x, p, g = triangle한 경우 - 2 rotate, recolor
- 시간복잡도 : (최대 2 rotate, color O(h) 상수 시간 ) -> O(log n)
+ 왜 O(log n)인가, 초기에 BST insert 연산을 호출할 때 O(log n)이기 때문이다.
만약 색상이 g와 g의parent의 색상이 R-R 과 같은 경우 rbtree를 만족할 때 까지 재귀적으로 restructing, recoloring한다.
+ 3-2-b의 경우를 볼 때 회전 한 번이 일어나면 3-2-a와 같은 경우가 되어 3-2-a를 한 번 더 수행한다.
삭제
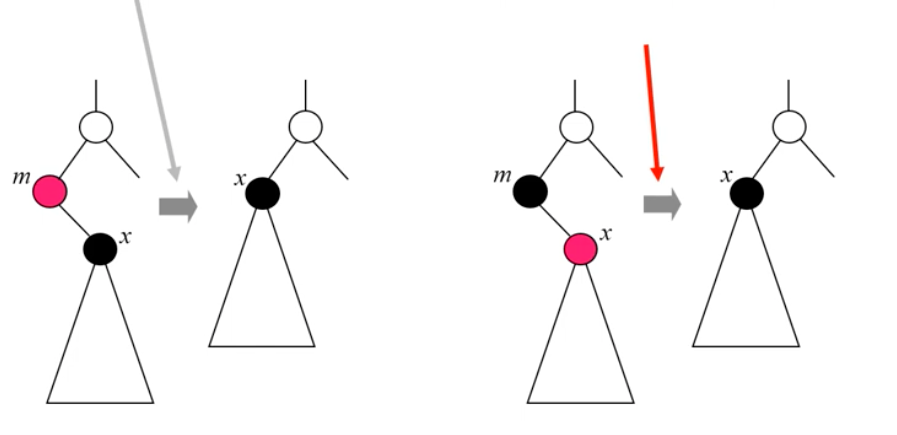
- 삭제 노드의 자식이 없거나 1개만을 가진 노드로 제한해도 된다.
- 삭제 노드를 m이라고 하자
- 삭제 노드가 레드이면 아무 문제 없다.
- 삭제 노드가 블랙이라도 (유일한) 자식이 레드이면 문제 없다.
삭제 연산 후 조건 위반되는 경우 처리 방법
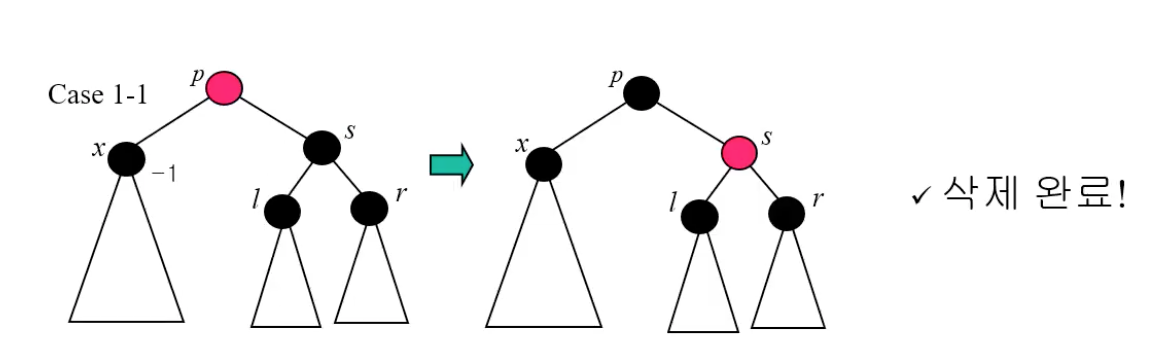
- case 1-1 : 부모 노드의 색이 빨간색일 때 : s의 노드 색상을 빨강으로 바꿔주고 p의 색상을 블랙으로 바꿔줘서 x 방향의 블랙 노드의 수가 유지되게 한다.
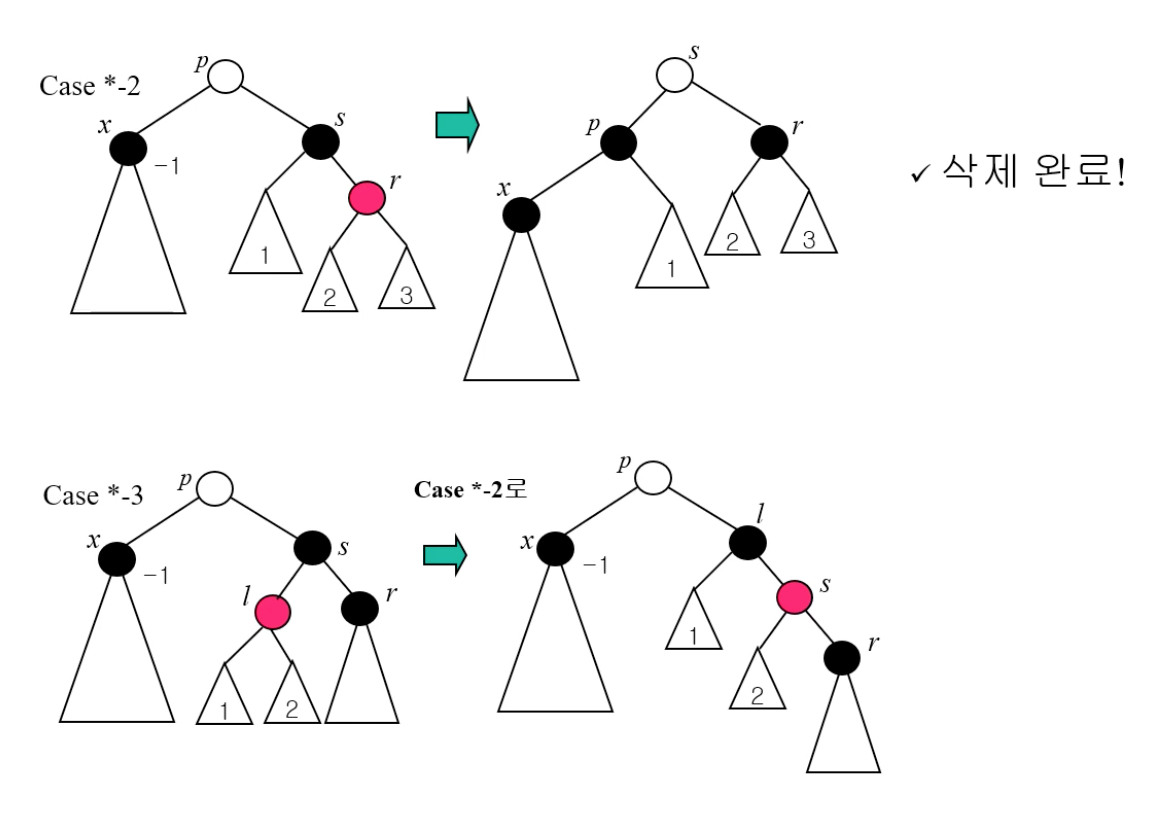
- case 1-2 : p의 색상과 상관없이 right-rotate를 해주고 기존에 p를 블랙으로, r도 블랙으로 바꿔주고 s의 왼쪽 서브트리를 p의 오른쪽 서브트리로 옮겨준다.
- case 1-3 : l, s, r을 linear하게 만들고 색상을 수정한 후 1-2의 수행방법을 진행한다.
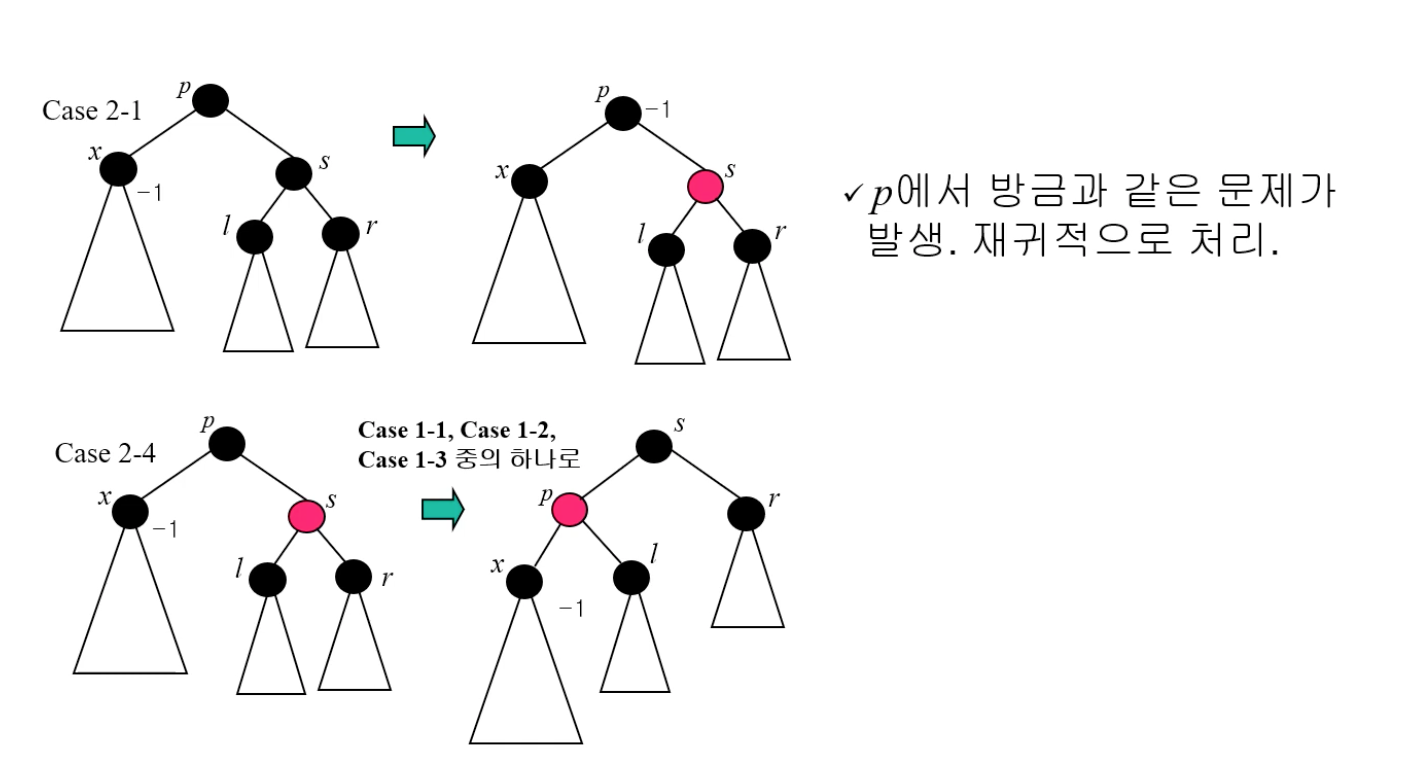
- case 2-1 : p에서 -1만큼 블랙 색상이 부족하기 때문에 s의 색상을 레드로 바꿔서 p의 위치에서 모두 -1만큼 모자르기 때문에 재귀적으로 p의 부모노드 방향으로 올라가서 다시 처리한다.
- case 2-4 : linear하게 만들고 rotate를 진행한다. x, p, l을 확인하여 case 1-1, -2, -3의 상황과 비교하여 진행한다.
색상의 위치와 방향이 반대일 경우 반대방향으로 동일하게 진행한다.