[BigData] Ch.1

인천대학교 최대진 교수님 강의를 개인적으로 정리한 글입니다.

Data Mining

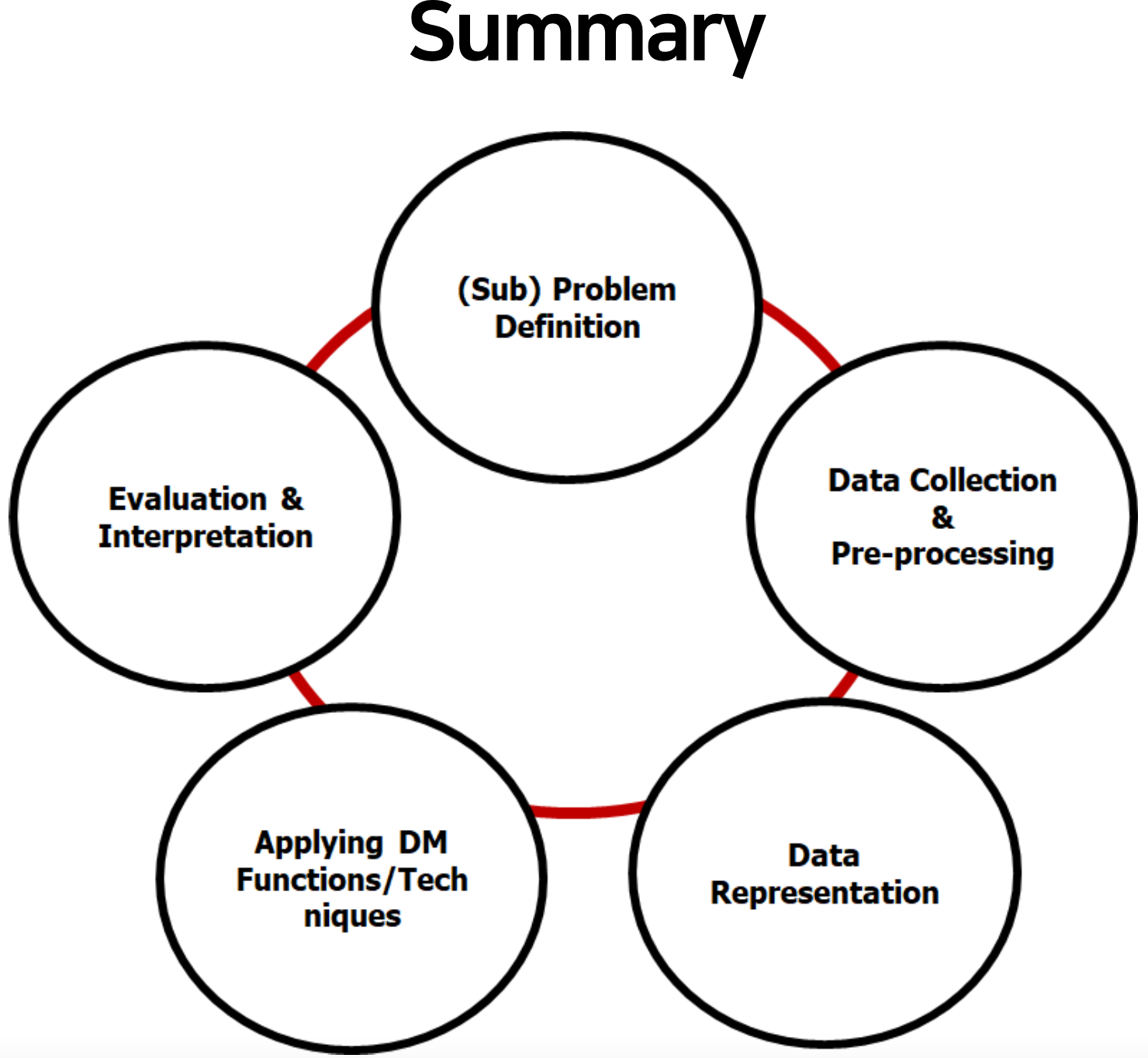
1. Problem Definition

• Define the problem as a scientific form
• Require domain knowledge as well as scientific problem solving capability

2. Data Collection

• Collecting data via

3. Data Representation

• Transforming a high-dimensional raw data into problem-relevant data
• Quantifying data with various techniques
  

MapReduce

Large scale computing for Data Mining
-> Using machine clusters is essential

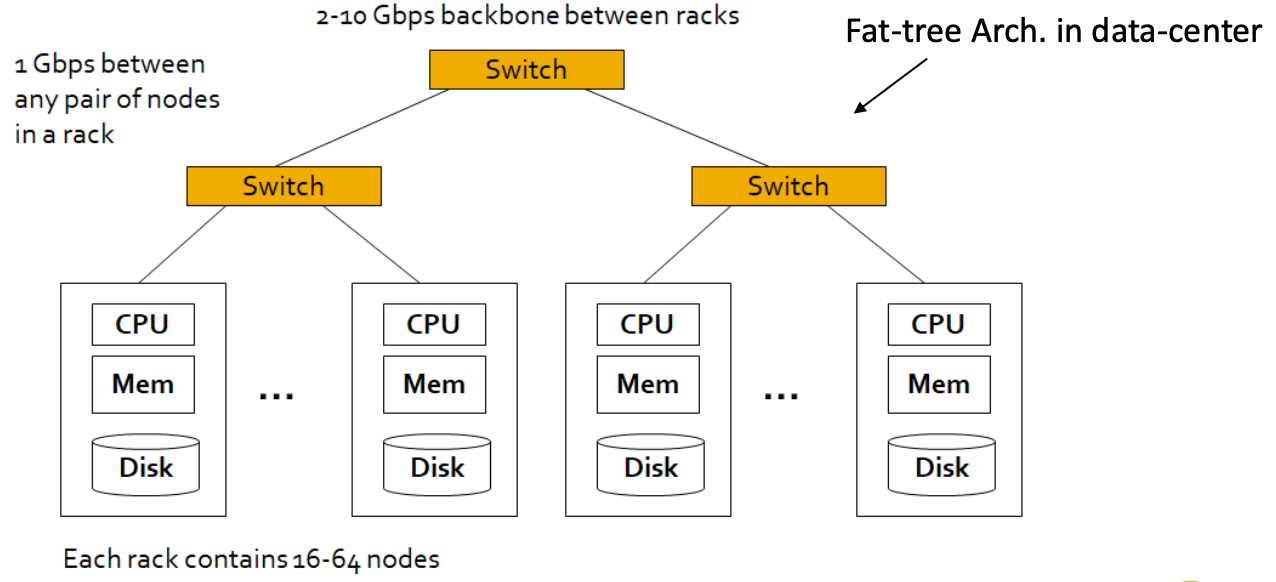
• Mining big data requires large-scale computing whose key component is Parallel programming
• MapReduce is Framework
  Apache Hadoop MapReduce, Amazon Elastic MapReduce

ex) Word Counting

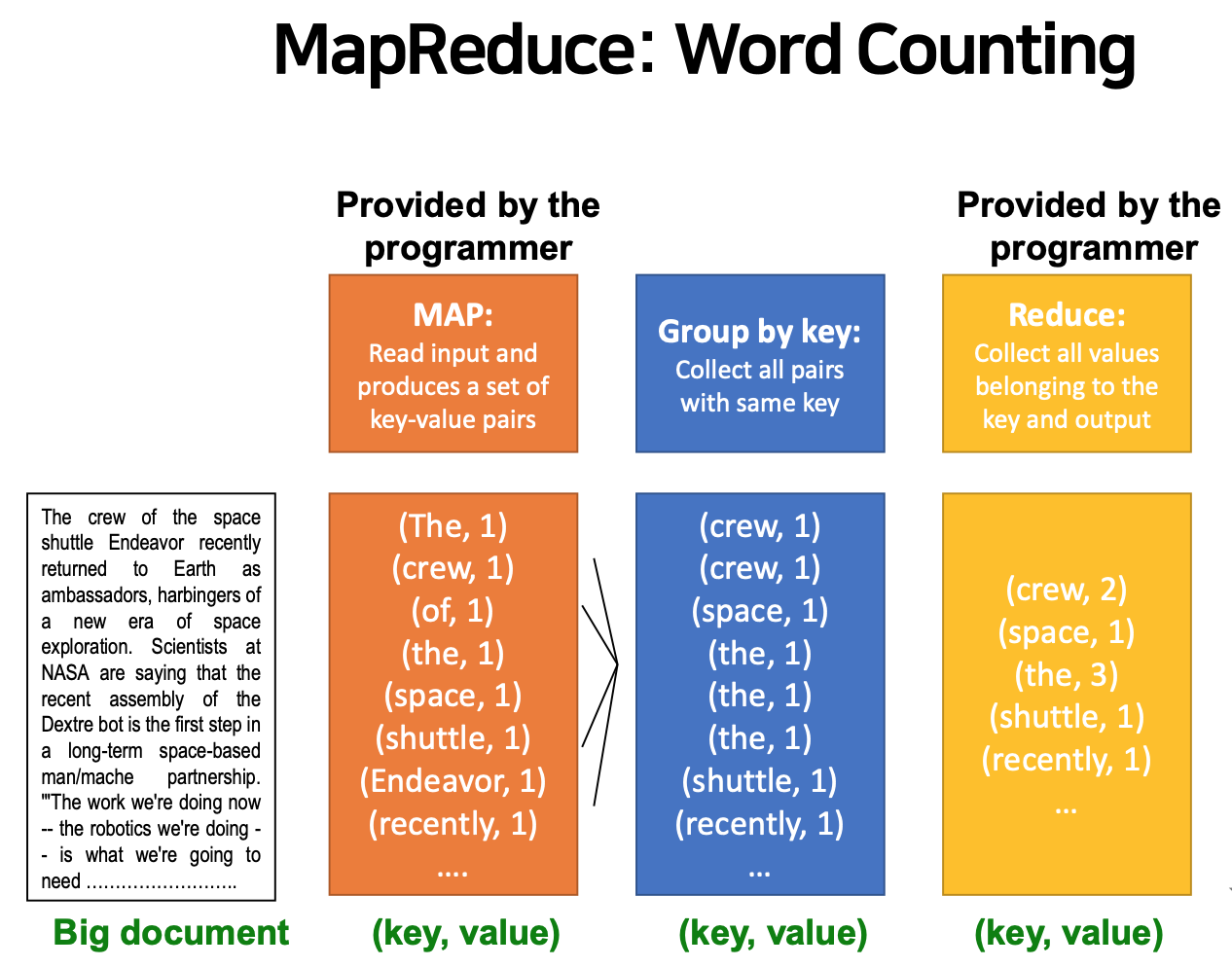
MapReduce Environment

• Partitioning the input data
• Scheduling the program's excution across of a set of machines
• Performing the group by key step
• Handling machine failures
• Managing required inter-machine communication

Using MapReduce Framework

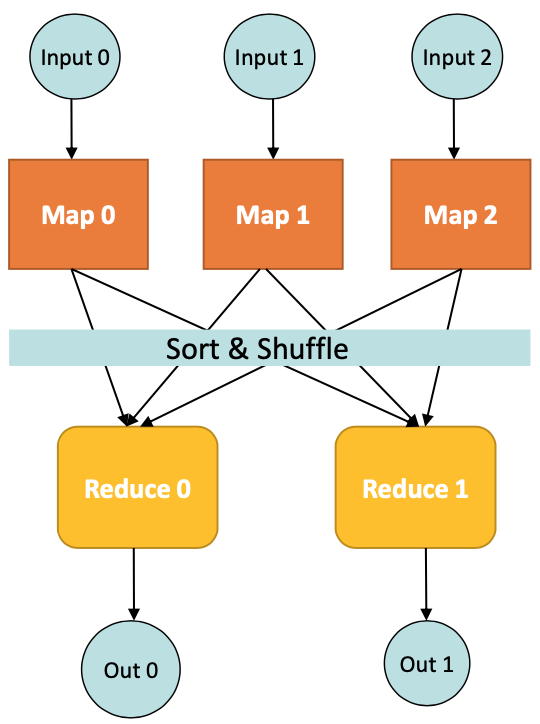
Data Flow

• Input and final output are stored on a distributed file system (DFS)

Stream Data

Big Data - Volumn, Velocity, Variety
high Velocity - Stream Data

Characteristics of Stream Data

• Size - Infinite, Burst (not equal speed, non-predictable) , Non-stationary
• only INSTATLY accessible
• Stream Management is important when the input rate is controlled externally

Applications

• Mining query streams
  ex) Google wants to know what queries are more frequent today than yesterday
• Mining click streams
  ex) Yahho wants to know which of its pages are getting an unusual number of hits in the past hour
• Mining social network news feeds
  look for trending topics on Twitter, Facebook
• Sensor Networks
  Many sensors feeding into a central controller
• IP packets monitored at a switch
  Gather information for optimal routing
  Detect denial-of-service attacks

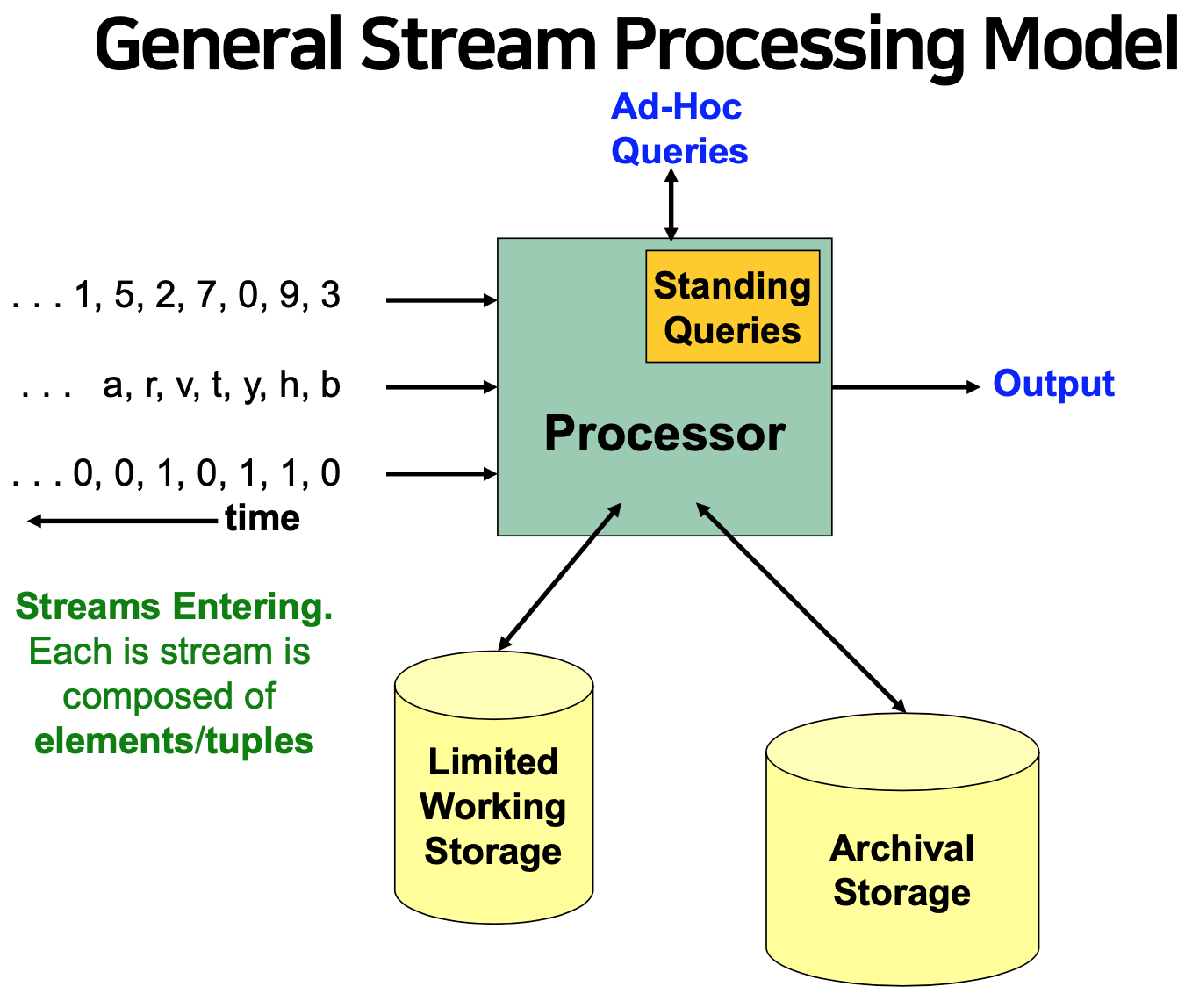
The Stream Model

• Input elements enter at a rapid rate, at one or more input ports
• The system cannot store the entire stream

SIDE NOTE : Online Learning
Online Learning enables a machine learning model to continously learn from the recent data stream

Example : Stochastic Gradient Descent (SGD)

Idea : Do slow updates to the model

Operations on Data Streams

• In conclusion, we have to choose a subset of input streams

1. Sampling data from a stream,
   • Construct a random sample.
2. Queries over sliding windows,
   • Number of ~~
3. Filtering a data stream,
4. Counting distinct elements,
5. Estimating moments,
6. Counting itemsets.

• Sampling data

fixed-size tuples

Why? Don't know length of stream in advance

Suppose at time n we havve seen s items

Reservoir Sampling

Algorithm

• Store all first s elements of the stream ot S
• Suppose we have seen n-1 elements, and now the n^th element arrives (n>s)

Sliding Window

• A useful model of stream processing is that queries are about a window of length N, the N most recent elements recieved.

Example Problem - Counting Bits

• Given a stream of 0s and 1s
• Be prepared to answer queries of form "How many 1s are in the last k bits? where K <= N

Real Problem :

• What if we cannot afford to store N bits?

DGIM Method does not assume uniformity

Exponential Windows

• Sampling a fixed propotion of stream
  Sample size grows as the stream grows
• Sampling a fixed-size sample
  Reservior Sampling
• Counting the number of 1s in the last N elements
  Exponentially

Filtering a Data Stream : Bloom Filter

Filtering Data Streams

• Each element of data stream is a tuple
• Given a list of keys S
• Determine which tuples of stream are in S
  + NOTE : It's different from from user-based sampling
  

Example Application: Email Spam Filtering

수 많은 이메일 중에서 정상으로 판정 된 메일은 스팸처리 X， 정상 처리된 이메일은 검색 없이 바로 보내고 싶다.

Bloom Fiter consists of

• An array of bits
• A number of hash functions

Two processes

• Setup process

• Lookup process

B[h(2)] = 1 : 내 이메일 (keys S)을 해쉬함수로 나온 숫자를 N 개 비트 배열의 위치를 구하고 1로 설정

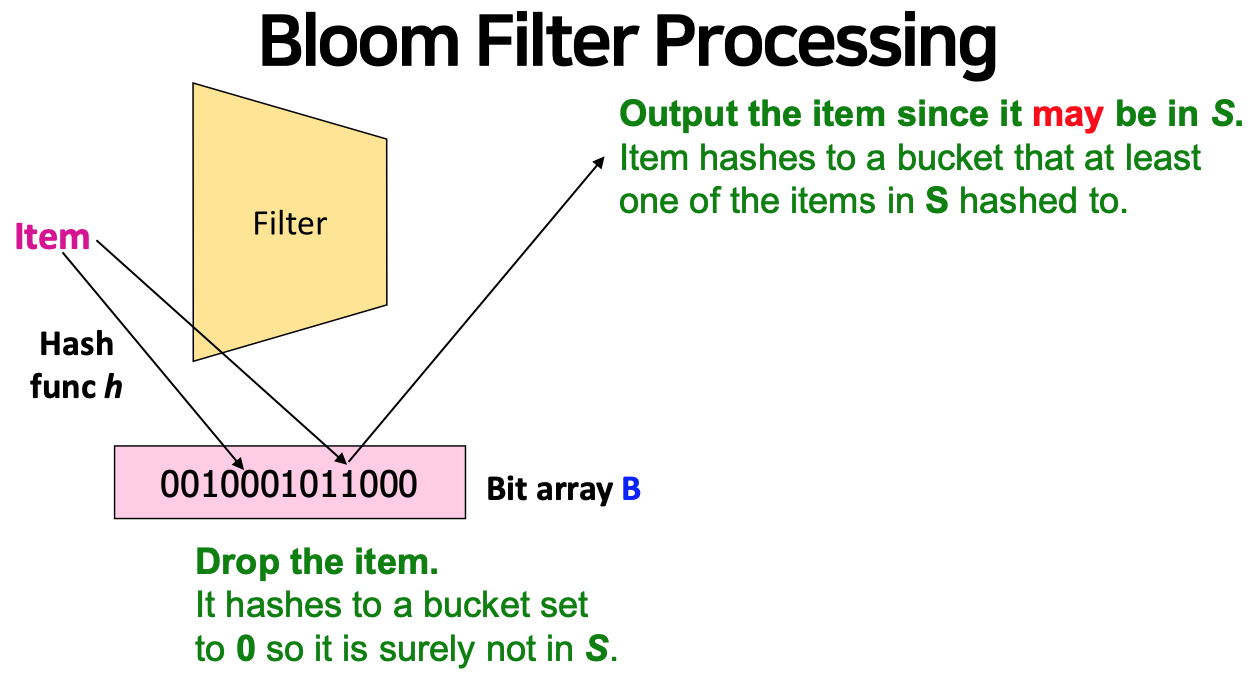
Creates false positives but no false negatives

• 정상 계정이 통과해야하는데 통과하지 못했다는 경우는 존재(create false positives), 비정상 계정이 통과하지 말아야 하는데 통과하는 경우는 없다.(no false negatives)

setup function에 여러 개의 hash function 존재.

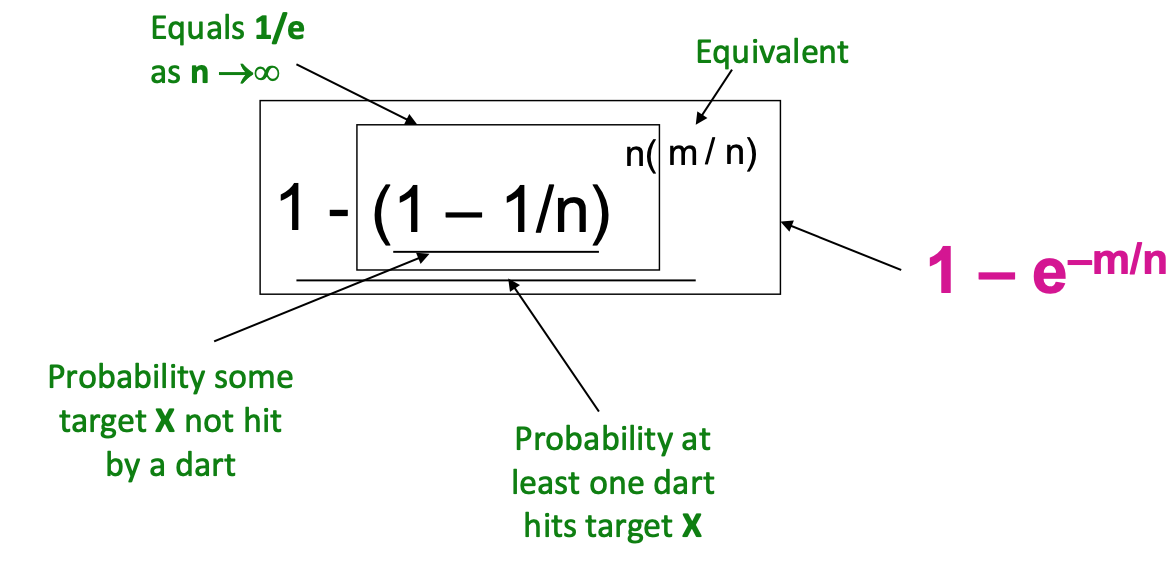
• 하나의 다트가 과녁에 맞을 확률 (1-1/n)

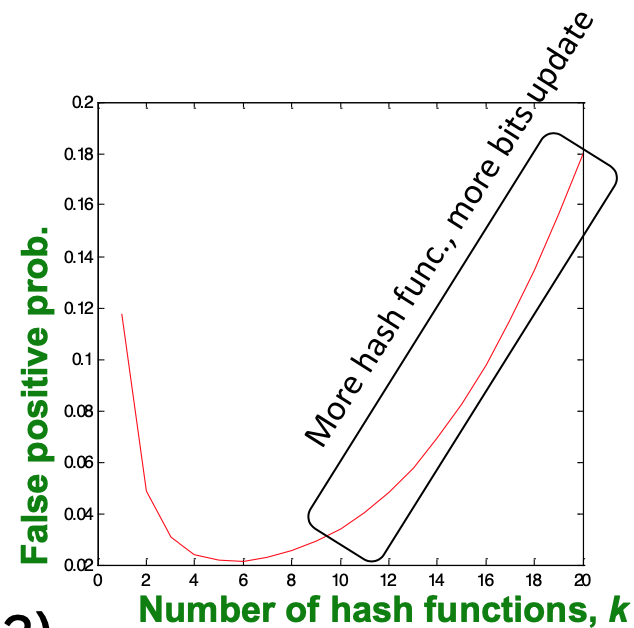
"Optimal" value of K: (n/m in(2))

Bloom filters guarantee no false negatives, and use limited memory

• Great for pre-processing before more expensive checks

Suitable for hardware implementation

• Hash function computations can e parallelized

hash function을 쓰는 이유 : 하드웨어딴에서 간단한 연산을 통해 쉽게 구현이 가능하기 때문이다 -> 속도가 매우 빠르다.

Counting Distinct Elements

Flajolet-Martin Approach

• Pick a hash function h that maps each of the N elements to at least log2 N bits
• For each stream element a, let r(a) be the number of trailing 0s in h(a)
• Record R
  새롭게 들어온 아이템을 hash running,
  r(a) = 오른쪽에서부터 연속적인 0의 갯수
  R= max r(a)

Computing Moments

i라는 아이템이 들어온 횟수 mi

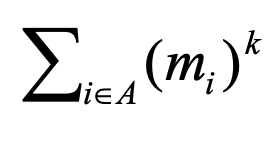
2nd moment : 아이템들이 얼마나 불균등하게 들어왔는가 (양)

AMS Method

공간이 한정하는 곳 까지 아이템을 최대한 저장하겠다.

Stream은 무한하지만 N개의 갯수를 안다고 가정하자,
N은 우리가 보고싶어하는 길이의 크기
0~N까지의 시간중 t라는 시점을 잡고 발견된 i의 갯수를 세어보자

-> 측정할수 있는 범위를 구하고 카운팅을 센 다음 식에 대입한다.

그렇다면 Stream은 무한한데 어떻게 측정하냐

Q. 미분 -> 기울기-> 지속적인 변경??

Counting Itemsets

item은 사실 tuple로 들어온다. 그럴 때 Itemset에 How to 적용
ex) 3개의 i가 있을 때 7개의 스트림 발생 -> i가 늘어남에 따라 다 저장이 불가능

Exponentially Decaying Windows

한 스탭이 넘어갈 떄 마다 1-c를 곱한다

빅데이터의 정의
주로 Volume, Velocity 에 대해서 배움
Stream 데이터에 대해서 어떤 식으로 샘플링, 추산, 계산한다.