
계기
현재 새마을 금고가 순수익의 다섯 배가 넘는 배당금을 주주들에게 지급하여 논란이 되고 있다.
2023년 새마을금고의 출자금 10조 9000억원 중 약 4800억원이 배당금으로 빠져나간 것이다.
본인이 투자하는 은행이 적자 전환이 되었다는 소식을 달가워할 주주는 없을 것이다.
그렇다면 회귀 분석을 통해 2025년, 2026년에 적자가 날지 미리 예상하는 방법은 없을까?
이를 위해 새마을금고에 대한 자료 조사를 해보았다.
새마을금고는 원래 적자를 냈는가?
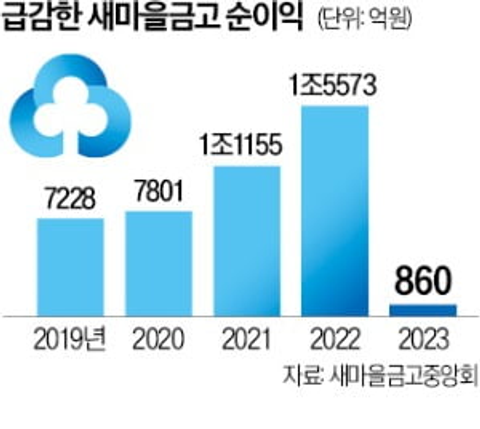
그렇지 않다.
그래프를 보면 2019년부터 쭉 증가하던 순이익이 2023년이 되자 급감했다는 것을 알 수 있다.
그렇다면 왜 2023년에 갑자기 순이익이 확 줄었는지를 확인해보아야 한다.
대손충당금으로 인한 적자 전환
 이코노미스트의 ‘새마을금고중앙회, 적자전환…지난해 순손실 2500억↑’ 기사
이코노미스트의 ‘새마을금고중앙회, 적자전환…지난해 순손실 2500억↑’ 기사
기사 전문에는 다음과 같은 내용이 있다.
매년 꾸준한 순이익 성장세를 이어오던 새마을금고중앙회가 지난해 적자전환했다.
부동산 프로젝트파이낸싱(PF) 등 대출채권의 부실 위험이 확대되면서,
대손충당금 적립 규모를 늘린 것이 원인으로 분석된다.
*대손충당금 : 대출 후 회수가 불가능하다고 판단된 금액
대출채권의 부실 위험이 확대되며 대손충당금의 적립 규모가 늘어난 것이 원인으로 분석된다고 한다.
그렇다면 부실채권에 따른 순이익을 분석해보면 적자를 예상할 수 있지 않을까?
자료조사
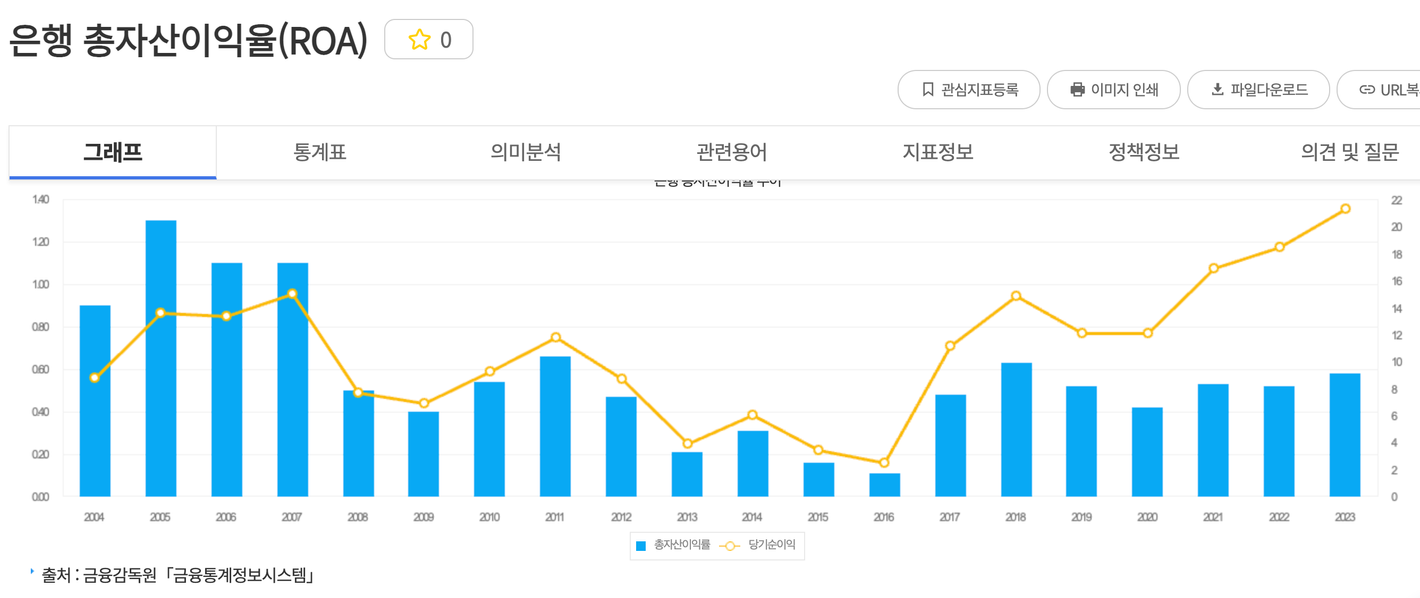
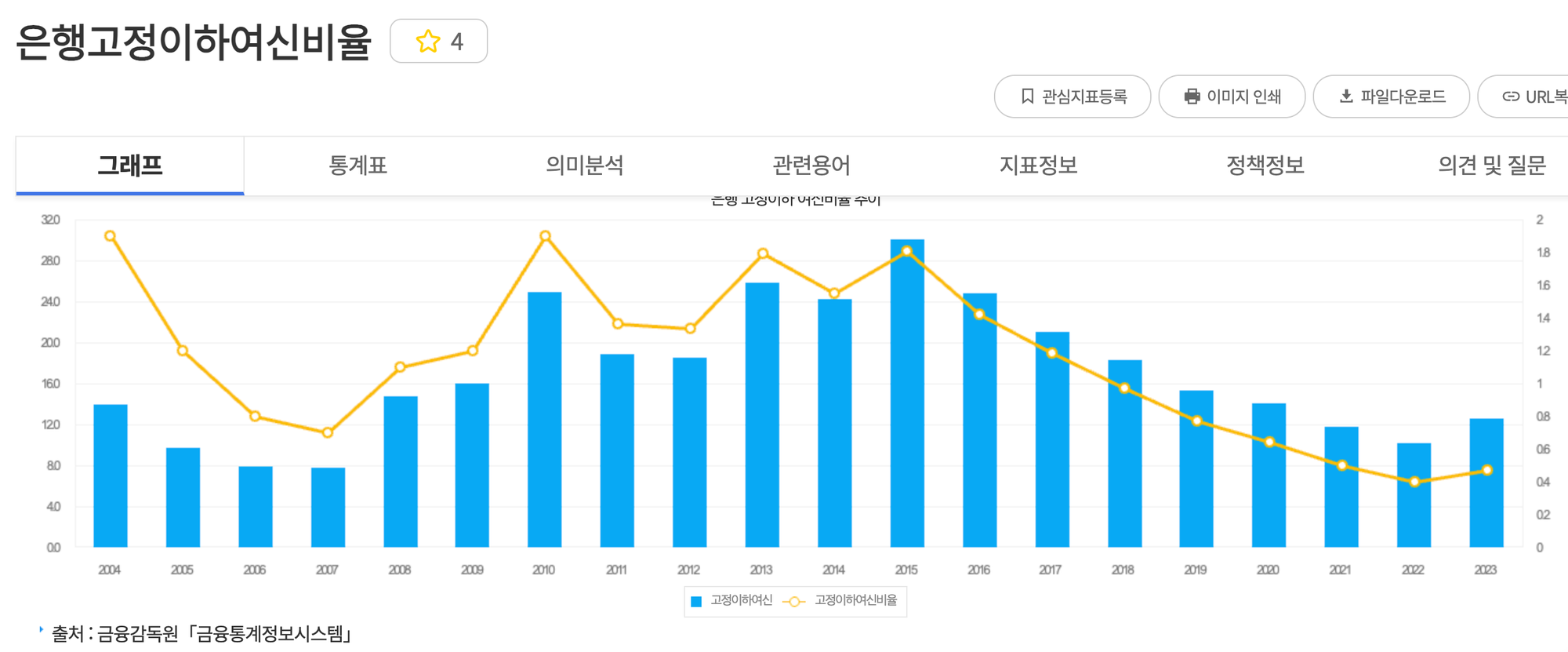
다음은 금융감독원에서 제공하는 은행의 총자산이익율과 고정이하여신비율이다.
언뜻 눈으로만 봐도 총자산이익율이 높을 땐 고정이하여신비율이 낮다는 것을 알 수 있다.
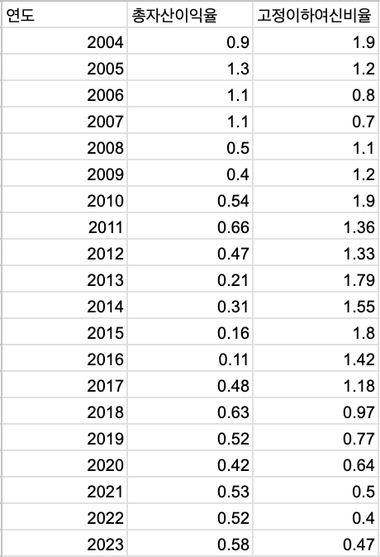
본격적으로 선형회귀분석을 위해, 이를 스프레드시트로 정리하고 시작해보자.
선형회귀분석
준비한 csv를 깃허브에 업로드한 후, 회귀 분석에 필요한 패키지들을 import해주자.
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np해당 데이터들의 로스값을 구하고 그래프로 나타내어 선형회귀가 가능한 데이터인지부터 확인하자.
def loss(x,y,beta_0, beta_1):
ms=np.sum((y - (beta_0 * x + beta_1))**2)
Loss=ms/len(x)
return Losscsv_file_path = "https:///...data.csv"
df = pd.read_csv(csv_file_path)
X = df['총자산이익율']
Y = df['고정이하여신비율']
train_X=X.values.reshape(-1,1)
train_Y=Y.values.reshape(-1,1)
lrmodel=LinearRegression()
lrmodel.fit(train_X, train_Y)
beta_0=lrmodel.coef_[0]
beta_1=lrmodel.intercept_
plt.scatter(X, Y)
predict=lrmodel.predict(train_X)
plt.plot(train_X,predict,'r')
print("beta_0:%.2f"%beta_0)
print("beta_1:%.2f"%beta_1)
print("Loss :%.2f"%loss(X,Y,beta_0,beta_1))beta_0 : -0.40, beta_1 : 1.38, Loss : 0.21
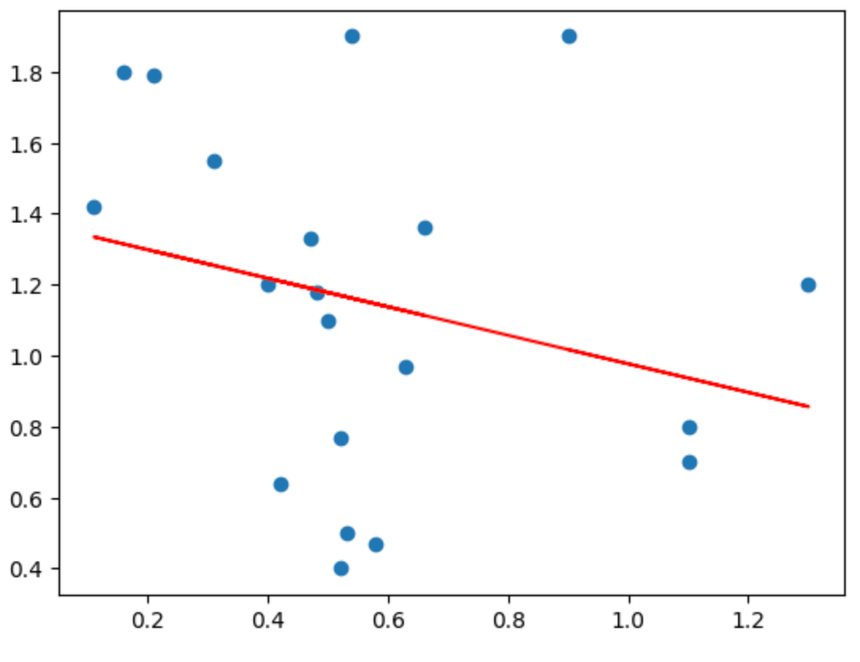
X축을 총자산이익율, Y축을 고정이하여신비율로 잡았다. 빨간 선을 자세히 보면,
고정이하여신비율이 감소함에 따라 총자산이익율이 증가한다는 것을 알 수 있다.
Loss값도 낮고, 최근 새마을금고의 적자 원인과 알맞은 그래프가 그려졌다.
또 가중치까지 찾았으니, 이제 실제 예측을 해보자.
lrmodel = LinearRegression()
lrmodel.fit(X.values.reshape(-1, 1), Y.values.reshape(-1, 1))
beta_0 = lrmodel.coef_[0][0]
beta_1 = lrmodel.intercept_[0]
def predict(예상고정이하여신비율, beta_0, beta_1):
value = float(예상고정이하여신비율)
return value * beta_0 + beta_1
예상고정이하여신비율 = input('고정이하여신비율을 입력해주세요: ')
predict_value = predict(예상고정이하여신비율, beta_0, beta_1)
print("예상되는 순수익: %.2f" % predict_value)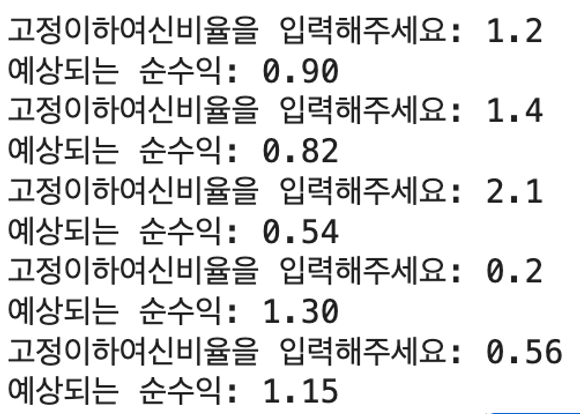
고정이하여신비율을 입력하면 이에 따른 순수익을 잘 예측한다~!!
회귀분석 개선시켜보기
회귀분석을 개선시켜보자. 여러가지 방법이 있는데 난 그중 다중 선형 회귀를 사용해 볼 것이다.
lrmodel = LinearRegression()
lrmodel.fit(X.values.reshape(-1, 1), Y.values.reshape(-1, 1))
beta_0 = lrmodel.coef_[0][0]
beta_1 = lrmodel.intercept_[0]
def expected_sales(예상고정이하여신비율, beta_0, beta_1):
value = float(예상고정이하여신비율)
sales = value * beta_0 + beta_1
return sales
예상고정이하여신비율 = input('고정이하여신비율을 입력해주세요: ')
expected_sales_value = expected_sales(예상고정이하여신비율, beta_0, beta_1)
print("예상되는 판매량: %.2f" % expected_sales_value)
y_pred = lrmodel.predict(X.values.reshape(-1, 1))
mse = mean_squared_error(Y, y_pred)
r_squared = r2_score(Y, y_pred)
print("MSE : %.2f" % mse)
print("결정계수 : %.2f" % r_squared)
다중 선형 회귀는 하나의 종속 변수를 여러 개의 독립 변수로 설명하는 회귀 분석 기법이다.
임의의 다항식을 사용하여 회귀 분석 모델을 개선하는 것은 다중 선형 회귀를 활용하는 한 가지 방법이다.
다항 특성 추가: 기존의 독립 변수들을 사용하여 다항식 특성을 추가한다.
ex) x에 대해 x^2, x^3 등의 다항식을 추가하여 새로운 독립 변수를 생성한다.
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X.values.reshape(-1, 1))
lr_model = LinearRegression()
lr_model.fit(X_poly, Y)
y_pred = lr_model.predict(X_poly)
mse = mean_squared_error(Y, y_pred)
print("Mean Squared Error:", mse)나는 2차식으로 바꾸어주는 sklearn의 PolynomialFeatures를 사용했다.
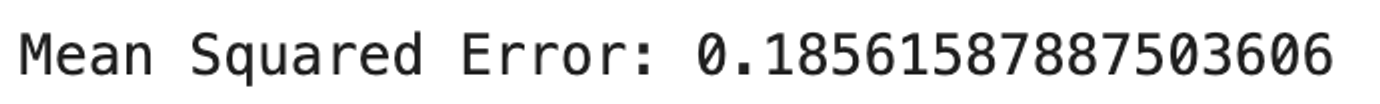
출력해보니 0.21이던 기존보다 더 0에 가깝게 나온다는 것을 알 수 있다!
기대 효과
- 재무 건전성의 이해 극대화
기업이 총자산이익율과 고정이하여신비율 사이의 관계를 더 잘 이해할 수 있다.
고정이하여신비율을 통해 미리 적자에 대비하여 재무 건전성을 유지하고 재무 리스크를 최소화할 수 있다. - 투자 결정의 강화
투자자들은 기업의 재무 건전성에 대한 추가 정보를 얻을 수 있다.
자산 배분 및 투자 결정을 보다 수학적인 근거에 입각하여 내릴 수 있다.

