문제

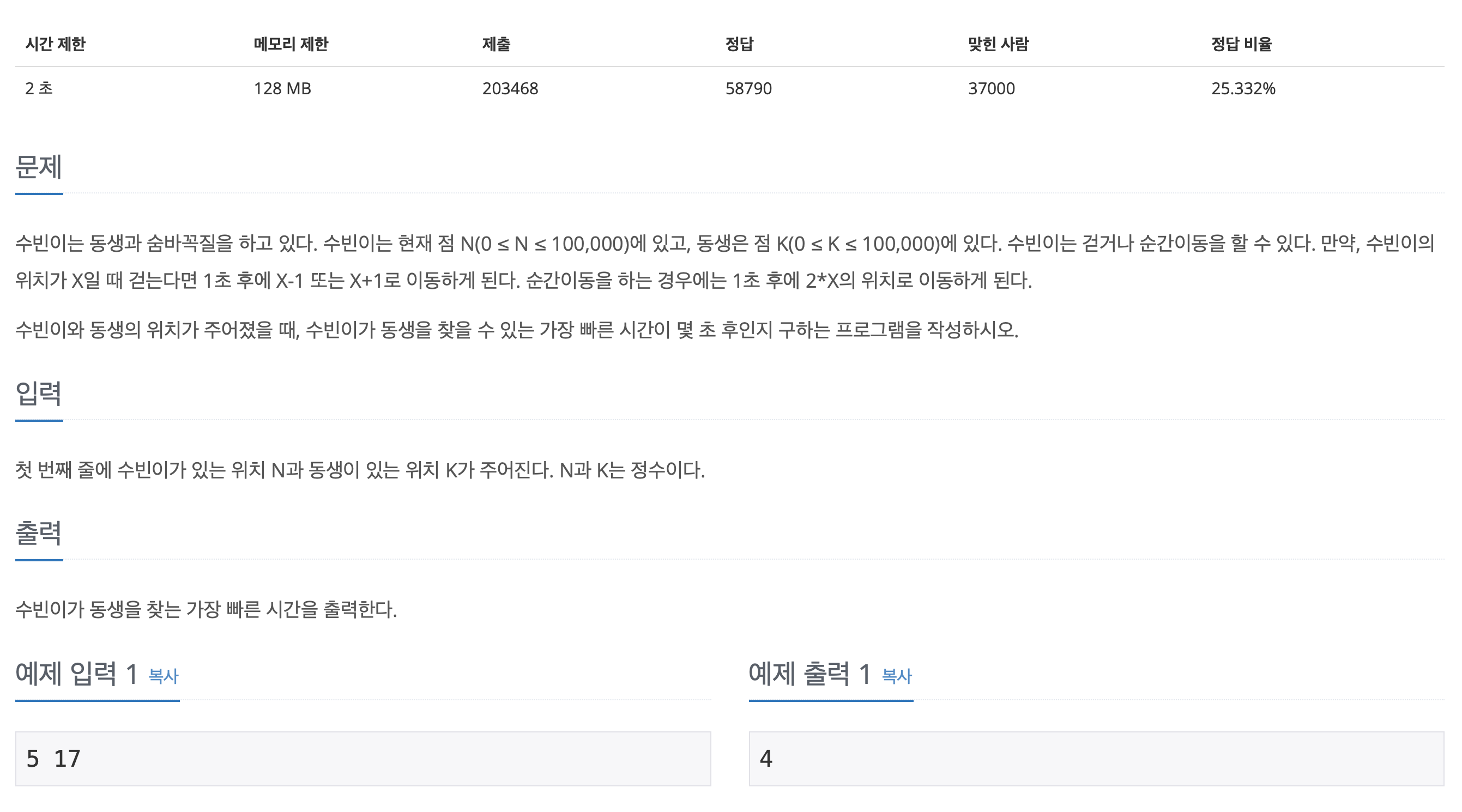
쉽게 말해서 N에서 K까지 최소시간 구학기이다.
N 포인트에서 5->10->9->18->17 순으로 가면 4초만에 K포인트로 갈수있다
N = 5
5 2 = 10 (1)
10 - 1 = 9 (2)
9 2 = 18 (3)
18 -1 = 17 (4)

맨처음에 DP로 접근하면 될거 같다는 생각이 들었지만... 1차원이라 애매했다...
삽질을 하다가 결국 힌트로 어떤 알고리즘이지 보니깐
그래프탐색이라는 걸 알았다.

일단 핵심은 K포인트로 가는 방법은 이 x * 2, x - 1, x + 1 밖에 없고 동일하게 1초 걸린다.

일단 bool타입인 vis 배열을 만들어 준다! 방문 여부를 체크해주는 용이다.
그러고 시작 포인트인 N값 즉 position이 될 값이랑 최초 시간인 0초를 pair<int,int>에 넣고 queue안에 넣어주고 vis[n] = true으로 시작 포인트 방문 체크 해준다.

while으로 queue가 빌 때까지 돌려준다.

if(!vis[pos * 2]){
            vis[pos * 2] = true;
            q.push({pos * 2,retTime+1});
        }

이런 식으로 pos * 2 위치를 방문을 하지 않았다면 방문처리를 해주고 큐안에 넣어준다.

pos + 1이랑 pos - 1도 똑같은 로직으로 해줬다.

pos가 목표 포인트인 k에 도달하면 걸린 시간을 출력준다

오답

out of boundary로 컴파일이 안 되길래 보니깐
범위는 100000였는데 순간이동으로 두배 곱하기 떄문에 범위도 두배로 해줬어야했다.
그래도 out if boundary가 떴는데. underflow하고 overflow 처리를 안 해줬다

 if(pos < 0 || pos > 100000) continue;

추가 해주니깐 정답...
제약 부분을 좀 더 디테일하게 못 챙겨준거 같아 민망스럽다

정답코드

#include <bits/stdc++.h>
using namespace std;
int n,k;
bool vis[200004];
queue<pair<int,int>> q;

void solve(){
    q.push({n,0}); // 시작점
    vis[n] = true;

    while(!q.empty()){
        int pos = q.front().first;
        int retTime = q.front().second;
        q.pop();
        
        // underflow + overflow check
        if(pos < 0 || pos > 100000) continue;
        
        if(pos == k) {
            cout << retTime;
            break;
        }
        
        if(!vis[pos * 2]){
            vis[pos * 2] = true;
            q.push({pos * 2,retTime+1});
        }

        if(!vis[pos-1]){
            vis[pos-1] = true;
            q.push({pos-1,retTime+1});
        }

        if(!vis[pos+1]){
            vis[pos+1] = true;
            q.push({pos+1,retTime+1});
        }

    } 
}

int main() {
    cin >> n >> k;
    solve();
    return 0;   
}