Heap Sort

본 문서는 2021년 12월 28일 에 작성되었습니다.

Dev 알고리즘 시리즈의 Sort 알고리즘 파트에서 다음을 알아보았습니다.

1. Selection Sort
2. Insertion Sort
3. Merge Sort

그 중 가장 효율적인 Merge Sort 를 LinkedList 와 결합하며 제자리 정렬화 시키거나,
Merge Sort 를 진행하다 일정 크기 아래에서는 Insertion Sort 를 사용하여 고도화 시키는 등의 방법은
유의깊게 볼만한 포인트였던 것 같습니다.

그렇다면 이 세 개의 공통점은 무엇일까요?
바로 숫자 비교 정렬 을 다루고 있다는 점입니다.

Heap Sort 또한 숫자 비교 정렬 을 다루며, Heap 자료구조를 통해서 구현됩니다.
따라서 Heap 을 모르고 있다면 Heap 포스트 를 참고하시길 바랍니다.

Heap Sort 란?

숫자 타입의 데이터를 정렬하기 위해서 Heap 이라는 자료구조의 특징을 사용한 것입니다.
기본 적으로 배열의 형태를 그대로 사용합니다.

자세한 내용은 아래의 두 파트를 자세히 읽어보시길 바랍니다.

1. 사전정의 및 구성요소
2. Heap Sort 위한 프로시저

---

사전정의 및 구성요소

앞서 알아본 Heap 포스트 에서 조금 더 이론적인 사전정의(분석) 을 언급하고
이에 따라서 우리가 알아볼 Heap Procedure 에 대해서 리스트 화 했습니다.

사전정의

Heap 의 특성은 다음과 같습니다.

1. 0 <= A.heap-size <= A.length
2. 0 인덱스부터 A.length 인덱스의 원소는 유효하나, A.heap-size 뒤의 원소는 힙이 아니다.
3. Heap 의 각 원소는 index 를 가진다.
   3.1. Left-Child.index 는 Parent.index 의 2배 이다.
   3.2. Right-Child.index 는 Parent.index 의 2배+1 이다.
4. Heap 의 각 원소는 height 를 가진다.
   4.1. height 는 각 노드에서 리프로 가는 가장 긴 하향 경로를 의미한다.

구성요소

Heap Procedure 에는 다음과 같은 것들이 있습니다.

1. Heap 유지 | MAX HEAPIFY procedure | O (lg n)
2. Heap 생성 | BUILD MAX HEAP procedure | O (n)
3. Heap 정렬 | HEAP SORT procedure | O (lg n)
4. Priority Heap 관련 | MAX HEAP INSERT, HEAP EXTRACT MAX, HEAP INCREASE KEY, HEAP MAXIMUM procedure | O ( lg n)

더하여 Java(jdk 1.8) 에는 정확한 Heap 을 지원하고 있지 않습니다.
따라서 Priority Heap 이나 Tree 구조를 활용하여 상속, 오버라이드 해야할 것 입니다.

---

Heap Sort 위한 프로시저

만약, 당신이 Java(jdk 1.8) 의 Collection Framework API 를 조금 뜯어보았다면,
아래처럼 캡슐화 되어 있는 프로시저를 경험해본 바가 있을 것이다.

우리가 원하는 Heap Sort 는 세 가지 세부 프로시저로 구성되어 있다.

1. MAX HEAPIFY | 한 부모 노드와 양가 자식들을 비교하여 자리를 교체하는 프로시저
2. BUILD MAX HEAP | 미정렬된 길이 n 의 입력 배열을 MAX HEAPIFY 를 이용해 HEAP 구조로 바꾸는 프로시저
3. HEAP SORT | 정렬된 HEAP 구조를 정렬된 길이 n 의 출력배열로 바꾸기 위한 프로시저

MAX HEAPIFY

위에서 언급한 Heap 의 특성을 유지하기 위한 프로시저 입니다.
이 프로시저는 다음의 세부 프로시저로 이루어져 있습니다.

1. 기준이 되는 Node 의 인덱스를 i, Left-Child 의 인덱스를 l, Right-Child 의 인덱스를 r, 최댓값의 인덱스를 largest 에 할당
2. A[ i ] 와 A[ l ] 를 비교하여 더 큰 노드의 index 를 largest 에 할당
3. A[ i ] 와 A[ r ] 를 비교하여 더 큰 노드의 index 를 largest 에 할당
4. largest 가 i 이면 프로시저 종료,
   그렇지 않으면 MAX HEAPIFY(largest) 호출 (재귀적 호출)

# MAX HEAPIFY 의사코드

MAX HEAPIFY (A, i)

l=LEFT(i)
r=RIGHT(i)

if L <= A.heap-size AND A[l] > a[i]
   largest=l
else
   largest=i

if R <= A.heap-size AND A[r] > a[i]
   largest=r

if largest!=i
   exchange A[i] with A[largest]
   MAX HEAPIFY(A.largest)

---

BUILD MAX HEAP

미정렬된 길이 n의 입력배열을 MAX HEAPIFY 를 이용해 HEAP 구조로 바꾸기 위한 프로시저입니다. 따라서 다음의 세부 프로시저로 이루어져 있습니다.

1. 첫 번째 원소의 index를 1으로 합니다.
2. 2 번째 원소를 부모 원소의 index*2 로 합니다.
3. 3 번째 원소를 부모 원소의 index*2+1 로 합니다.
4. 4,5 번째 원소를 부모 원소(2번째 원소) 의 index*2 로 합니다.
5. 6,7 번째 원소를 부모 원소(3번째 원소) 의 index*2+1 로 합니다.
6. 오름차순 행렬을 완벽 이진 트리로 변경이 끝났으면 index 가 가장 큰 부분부터 1까지 -1 씩 내려오며 MAX HEAPIFY 프로시저를 진행합니다.
7. 모든 절차가 종료되면 완벽한 HEAP 자료구조의 데이터가 형성됩니다.

# BUILD MAX HEAP 의사코드

BUILD HEAP (A, i)

A.heap-size=A.length;

for i=|A.length/2| downto 1
   MAX HEAPIFY(A, i)

# BUILD HEAP 도식화

---

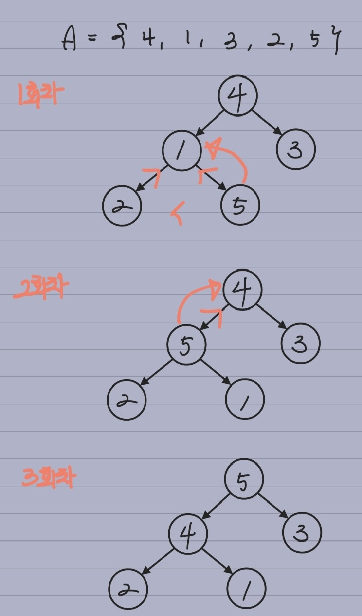
HEAP SORT

정렬된 HEAP 구조를 정렬된 길이 n의 출력배열로 바꾸기 위한 프로시저입니다.
최초 미정렬된 입력배열 A[a,b,c,...,n] 은 BUILD MAX HEAP 을 통해 완벽 이진 트리 구조의 최대 힙으로 변경되었을 것입니다. 이를 일정한 프로시저를 이용하면 오름차순이 완료된 출력배열 A'[1,2,3,...,n] 을 반환받게 할 수 있습니다.

다음과 같은 프로세스로 진행된다.

1. 초기 heap-size 와 동일한 길이를 가지는 반환용 배열 A 를 만든다.
2. Heap 구조 최상위의 부모를 A 배열의 마지막 자리부터 채우고 해당 자리에 (구조상) 최솟값을 넣는다.
3. 최상위 부모의 자리에 원소를 둘 친구를 MAX HEAPIFY 를 실행한다.
4. 2~3 과정을 반복하여 최종적으로 오름차순 정렬이 완료된 출력배열 A'을 반환받는다.

# HEAP SORT 의사코드

HEAP SORT (A, i)

BUILD MAX HEAP(A, i)

for i=A.length downto 2
   exchange A[1] with A[i]
   A.heap-size=A.heap-size-1
   MAX HEAPIFY (A, i)

---

결론

위의 세 프로시저를 통합한 결론입니다.

우리는 결국 일반적인 배열의 형태를 데이터를 다룰 것입니다.
Heap Sort 란 결국 위에서 언급한 세 가지 프로시저를 이용한 비교 정렬 방법인 것입니다.
그러나 그 특이성 때문에 Heap 이라는 구조로 배열을 변경해야 할 필요성이 있습니다.

따라서 Heap 의 특성인 최댓값 및 최솟값 등의 이유 혹은 특별한 이유 가 아니라면,
Heap Sort 를 사용할 이유는 없을 것 같습니다.

또한 Heap 의 대중적인 응용인 Priority Queue 가 있으니 이를 확인해보자

---

Ref

[자료구조] Heap 이란?
[알고리즘] Heap Sort 란?
Heap Sort - The Sorting Algorithm Family Reunion