[Canvas] #02. 삼각함수, 원, 좌표계

undefcat·2020년 3월 18일

목록 보기

2/6

삼각법

Trigonometry is a branch of mathematics that studies relationships between side lengths and angles of triangles. - wikipedia

삼각법은 삼각형의 각과 두 변의 관계를 연구하는 수학의 한 분야이다. 그 중에서도 프로그래밍에서 자주 사용되는 것은 직각삼각형의 삼각비와 삼각함수이다.

삼각함수

일반적인 고등교육과정을 나온 사람들이라면 다들 sin cos tan는 한 번쯤 들어봤을 것이다. 또, 자세히 기억은 안날 수도 있지만 얼싸안코 올싼타코 등으로 뭔가를 외워본 기억이 있을 것이다.

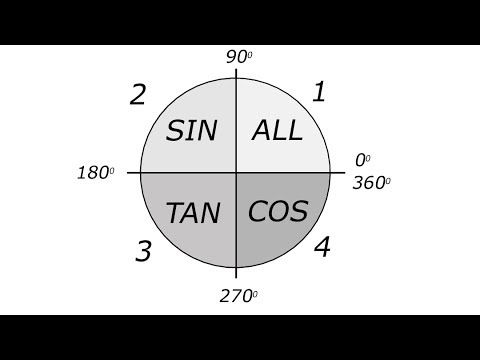
아무튼, 삼각함수는 sin cos tan 함수로 정의되는데, 이 때 함수의 매개변수 값이 바로 각도다.

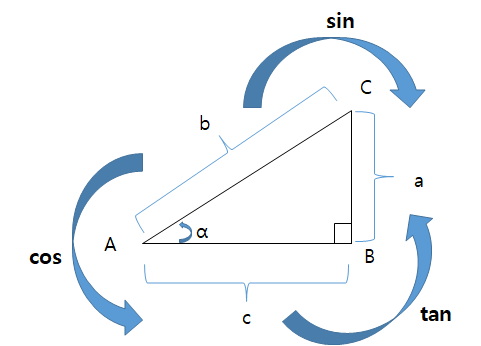
sin cos tan의 정의는 위의 이미지와 같다. 직각삼각형에서 빗변과 밑변이 이루는 각을 기준으로 각 두 변의 비율을 각각 sin cos tan로 정의한 것이다.

왜 직각삼각형에서 이 삼각함수의 값이 중요할까? 직각삼각형에서는 두 변의 비율과 각도의 값이 항상 일정하다. 즉, 말 그대로 삼각함수다.

두 변과 각이 이루는 값이 항상 일정하다는 의미는, 이 3개의 미지수 중 2개를 알고 있다면 다른 하나는 자연스럽게 결정된다는 의미다.

그럼 대체 얘네를 언제 사용할까? 그에 앞서, 원에서의 삼각함수를 살펴보자.

원과 삼각함수

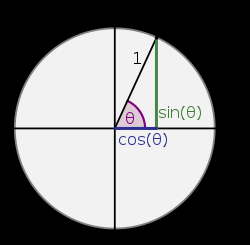
여기 반지름이 1인 원이 좌표평면 위에 있다고 하자. 이 경우, 그림에서 원 위의 점의 좌표 (x, y)는 어떻게 될까?

cosθ = x/1 이므로 따라서 x = cosθ가 된다. 마찬가지로 sinθ = y/1이므로 y = sinθ가 된다.

그렇다면, 반지름이 r인 원의 경우 x = r⋅cosθ, y = r⋅sinθ가 된다.

좌표평면 위의 어떤 점 (x, y)가 있다고 하자. 원점과 이 점의 좌표의 거리는 피타고라스 정리에 의해 쉽게 구할 수 있다.

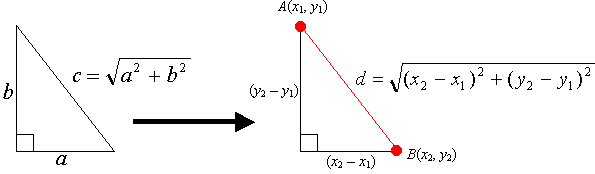
그 거리값을 r이라고 하면, 원점과 이 점과의 각도를 우리는 바로 구할 수 있다. 바로 방금 위에서 했던 원의 문제를 푸는 것과 똑같기 때문이다.

결국 좌표평면에서 원점을 기준으로 어떤 특정한 점의 위치를 알고 있다면, 원점과 이 위치와의 각도를 알 수 있다.

더 나아가, 두 점 간의 관계도 쉽게 구할 수 있다. 점 A, B가 있을 때 좌표계에서 A와 B의 서로의 각도를 구하고자 한다면 단순히 두 점 중 하나를 원점으로 평행이동 시키는 변환을 거치면 된다.

그러면 결국, 원점과 평행이동 된 점에 대해 위에서 했던 방법과 똑같은 방법으로 거리, 각도를 구할 수 있게 된다!

컴퓨터의 좌표계

컴퓨터의 좌표계는 우리가 수학에서 배워왔던 좌표계와는 사뭇 다르다.

일반적인 수학 좌표계는 알다시피 원점을 기준으로 위로 가면 y값이 증가한다. 하지만 컴퓨터 세계에서는 그렇지 않다. 컴퓨터에서의 원점은 보통 왼쪽 상단이다. 이는 HTML과 CSS를 하는 사람이라면 아주 잘 알고 있다. CSS로 위치를 잡을 때, offset parent의 원점 기준은 항상 왼쪽 상단이었으니 말이다.

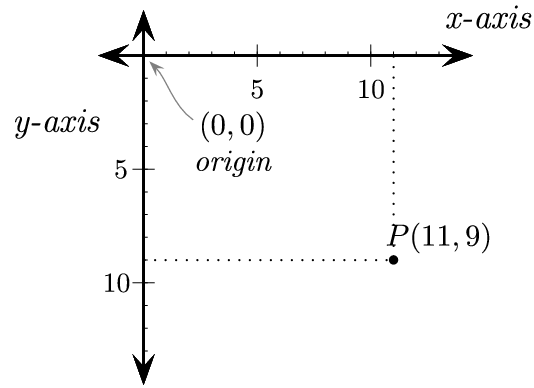
즉, 컴퓨터 세계에서는 보통 왼쪽 상단이 (0, 0)이므로 오른쪽으로 갈수록 x값이 증가하는 것은 똑같지만, 반대로 아래로 내려가면 y값이 증가한다.