Line
이번엔 선을 그려보자. 선 역시 path를 이용한다.
우선 beginPath로 path를 시작한 후, 선을 어디서부터 그릴지 그 시작점을 moveTo 메서드로 정해준다. moveTo 메서드의 인터페이스는 아래와 같다.
void ctx.moveTo(x, y)매우 간단하다. 단지 x y 좌표를 정해주기만 하면 된다.
ctx.beginPath()
ctx.moveTo(200, 200)그 뒤, 해당 점으로부터 시작해서 어디로 선을 이을지는 lineTo 메서드를 이용한다. 메서드의 인터페이스는 아래와 같다.
void ctx.lineTo(x, y)역시나 매우 간단하다.
ctx.lineTo(300, 300)우린 방금 (200, 200)에서 (300, 300)으로 이어지는 대각선을 하나 그렸다. 아직까진 보이지 않는다. 이 path에 선을 칠해주자. 선을 표시하려면, 기본적으로 선의 두께와 선의 색 등이 필요할 것이다.
선의 두께는 lineWidth 프로퍼티로 정해줄 수 있다. 그리고 선을 그리는 메서드는 stroke 메서드다.
stroke 메서드는 매개변수로 path를 받을 수 있지만, 이는 지금 사용하지 않겠다.
ctx.lineWidth = 10
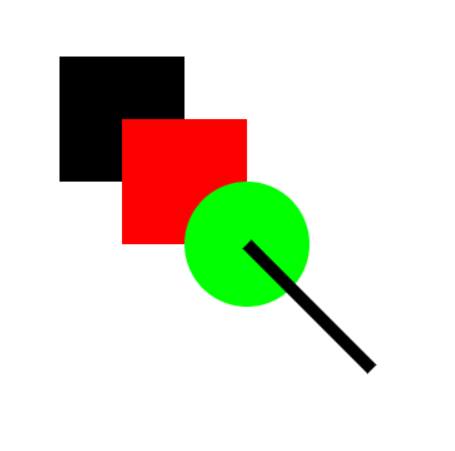
ctx.stroke()이전 챕터에 이어서 지금까지의 결과는 아래와 같다.
다시, 사각형
이전 챕터에서 fillRect를 이용해서 사각형을 그렸는데, 사실 엄밀히 말하면 이는 사각형을 그린 것이 아니다. 단지 사각형으로 색을 채웠을 뿐이다.
기본적으로 캔버스에서는 path를 이용해 선을 그리고, 이 선에 대해서 stroke로 선을 칠하거나 fill을 이용해서 닫힌 path에 색을 채운다.
fillRect를 path와 fill을 이용해서 표현해보자.
ctx.beginPath()
ctx.moveTo(300, 300)
ctx.lineTo(400, 300)
ctx.lineTo(400, 400)
ctx.lineTo(300, 400)
ctx.fillStyle = `rgba(0, 0, 0, 1)`
ctx.fill()
ctx.closePath()우선 (300, 300)부터 시작해서 가로/세로 100만큼의 사각형을 그렸다. 여기서 lineTo로 다시 (300, 300)으로 돌아가지 않았는데, 이는 closePath를 호출하면 자연스럽게 path가 시작된 곳으로 이어지기 때문이다.
사각형은 자주 그릴 것이므로, rect 메서드가 이미 존재한다.
void ctx.rect(x, y, width, height)위에서 했던 것과 똑같이 하자면
ctx.beginPath()
ctx.rect(300, 300, 100, 100)
ctx.fillStyle = `rgba(0, 0, 0, 1)`
ctx.fill()
ctx.closePath()이렇게 편하고 직관적으로 할 수 있다.
현재까지의 이미지는 아래와 같을 것이다.
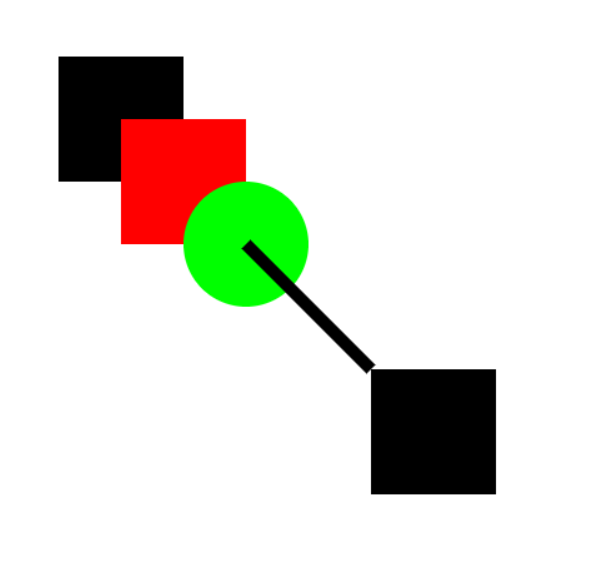
우린 이제 캔버스에 기본적인 선, 사각형, 원을 그릴 수 있게 되었다!
Vector
캔버스에 움직이지 않는 그림만 그리면 별로 재미가 없을 것이다. 캔버스를 사용하는 이유 중 하나는, 다채로운 애니메이션 효과를 주기 위함일 것이다.
컴퓨터 프로그래밍에서 움직임을 표현하는 것은 현실 세계에서 움직임을 계산하는 것과 크게 다르지 않다.
우리는 물리시간에 위치, 속도, 가속도의 개념을 배웠다. 이렇게 현실세계에서 사용되는 개념을 컴퓨터에서도 똑같이 활용하면 된다.
위치는 너무 쉽다. 좌표평면 위에 특정한 (x, y)의 값이 바로 위치가 된다.
속도는 위치의 변화량이다. 특정 단위시간동안 얼마나 위치가 바뀌었는지를 나타낸다.
가속도는 속도의 변화량이다. 특정 단위시간동안 얼마나 속도가 바뀌었는지를 나타낸다.
속도와 가속도는 벡터로 나타낼 수 있다. 벡터라는 말에 너무 쫄지 말자. 이는 그저 크기와 방향을 포함하는 개념이라는 것만 알면 된다.
우리는 2차원 캔버스를 가지고 놀 것이므로, 우리가 사용하는 벡터 개념도 역시 2차원이다. 벡터는 위치값과 마찬가지로 (x, y)로 나타낸다.
속도 벡터
속도는 특정 단위시간동안 얼마나 위치가 바뀌었는지를 나타낸다고 했다. 예를 들어, 속도 벡터가 (1, 1)이라고 하자.
그리고, 최초의 위치를 (0, 0)이라고 하자. 다시, 속도는 단위시간동안의 위치의 변화량이라고 했다. 이 위치에 1초마다 (1, 1)이라는 속도 벡터를 더해보자.
- 0초 뒤, 위치는 (0, 0)일 것이다.
- 1초 뒤, 위치는 (1, 1)일 것이다.
- 2초 뒤, 위치는 (2, 2)일 것이다.
- 3초 뒤, 위치는 (3, 3)일 것이다.
- 4초 뒤, ...
(1, 1)이라는 속도벡터는 위치의 변화량이라고 했다. 위의 예제에서는 단위시간이 초였을 뿐이다. 1초마다 위치값에 속도 벡터값을 단순히 더했을 뿐이다. 이게 벡터다.
벡터는 크기와 방향을 포함하는 개념이라고 했다. 좌표평면에서 벡터는 화살표로 보통 표현한다.
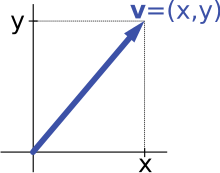
좌표평면의 원점을 기준으로 (x, y)까지의 길이가 크기이고, 각도가 방향이다.
실제로 위치 (0, 0)에 속도 벡터 (1, 1)을 매 초 더하면 위치값이 루트2씩 커지고, 방향은 45°라는 것을 알 수 있다. 이는 속도 벡터와 정확히 일치한다. 이를 단순히 받아들이면 된다.
가속도 벡터
가속도는 속도의 변화량이다. 위치 (0, 0)과 속도 벡터 (1, 1), 그리고 가속도 벡터 (1, 1)이 있다고 하자.
이제 매 초마다 위치가 어떻게 변하는지 생각해보자.
- 0초 뒤, 위치는 (0, 0)일 것이다.
- 0초 뒤, 속도 벡터는 (1, 1)일 것이다.
- 1초 뒤, 위치는 (1, 1)일 것이다. 이는 (0, 0)에 속도 벡터 (1, 1)을 더한 값이다.
- 1초 뒤, 속도 벡터는 (2, 2)일 것이다. 이는 (1, 1)에 가속도 벡터 (1, 1)을 더한 값이다.
- 2초 뒤, 위치는 (3, 3)일 것이다. 이는 (1, 1)에 속도 벡터 (2, 2)를 더한 값이다.
- 2초 뒤, 속도 벡터는 (3, 3)일 것이다. 이는 (2, 2)에 가속도 벡터 (1, 1)을 더한 값이다.
- 3초 뒤, 위치는 (6, 6)일 것이다.
- 4초 뒤, 위치는 (10, 10)일 것이다.
- 5초 뒤, 위치는 (15, 15)일 것이다.
- 6초 뒤, ...
매우 쉽다. 매 초마다 위치에는 속도 벡터값을 더한다. 그리고 속도에는 가속도 벡터값을 더한다.
다음엔?
우린 이제 path개념으로 선, 도형을 그릴 수 있게 되었고, 벡터 개념을 이용해 움직임을 표현할 수 있게 되었다. 이제 남은 것은 이 개념을 이용해 실제로 캔버스로 표현하기만 하면 된다.
다음 챕터에서는 도형을 움직여 볼 것이다.

