14. 세그먼트 트리

구간 합

구간 합은 여러 개의 데이터가 연속적으로 존재할 때 특정한 범위의 데이터의 합을 구하는 것을 의미

선형적으로 구간 합 구하기

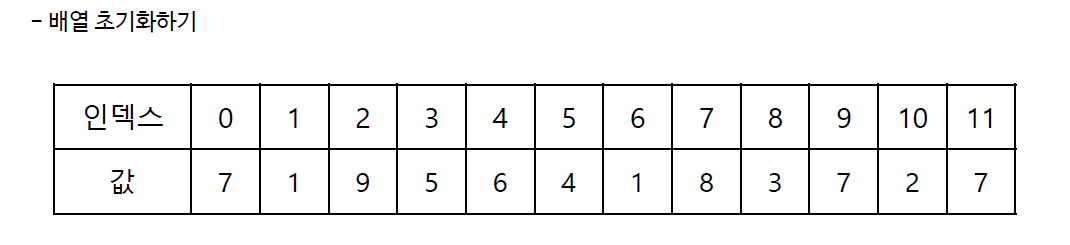
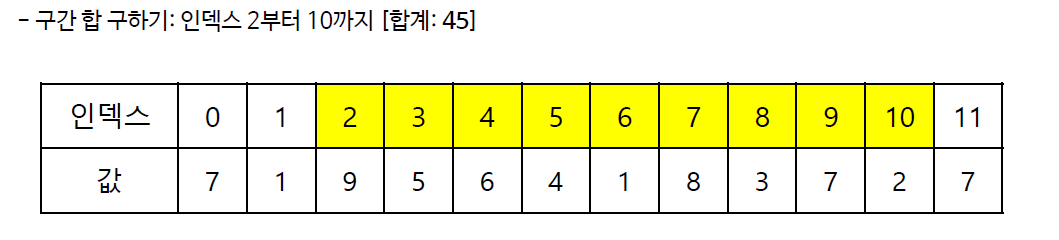
선형적으로 구간 합을 구하는 과정은 O(N)의 시간 복잡도를 가짐

트리구조로 구간 합 구하기

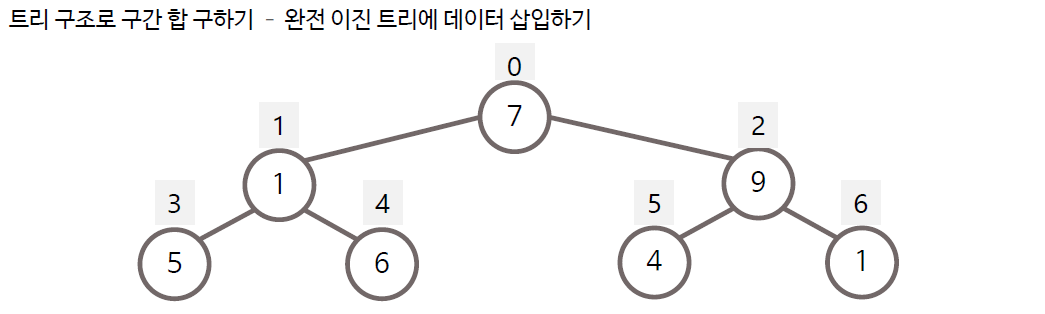
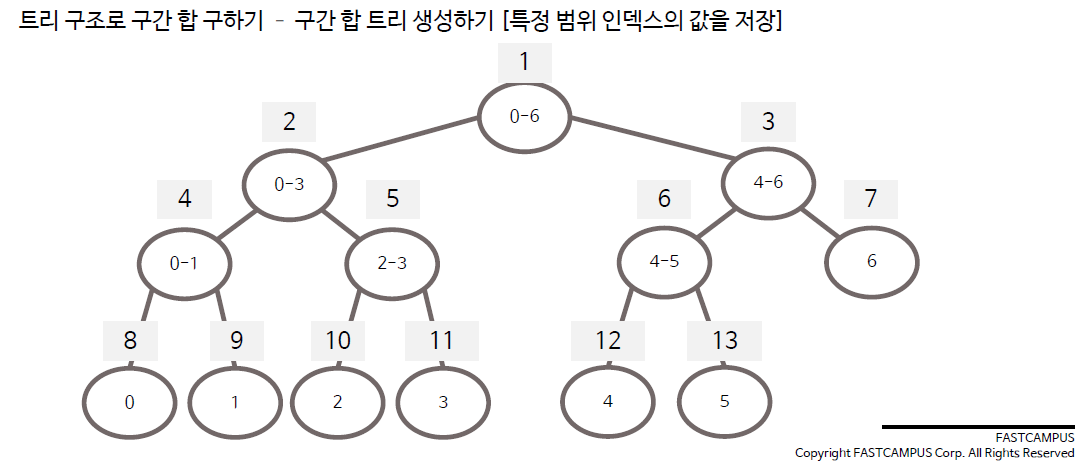
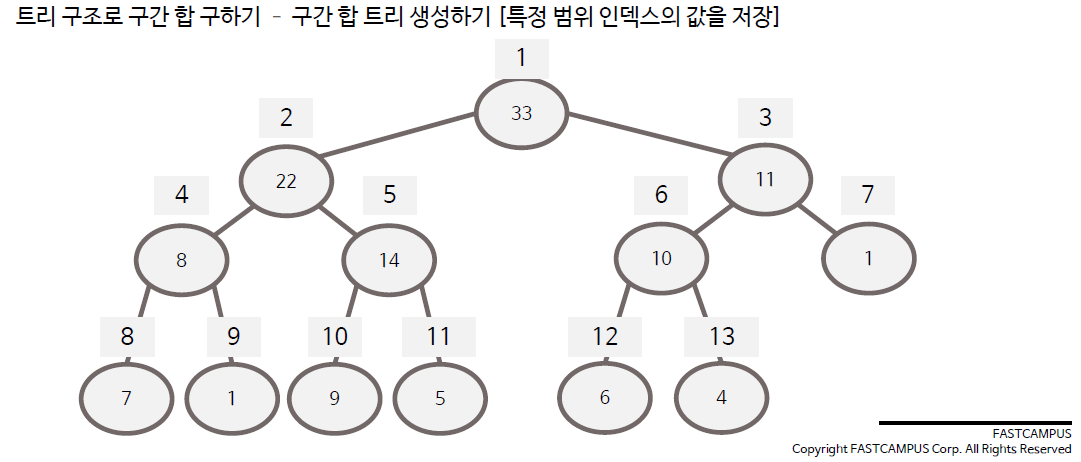
구간합 계산 방법

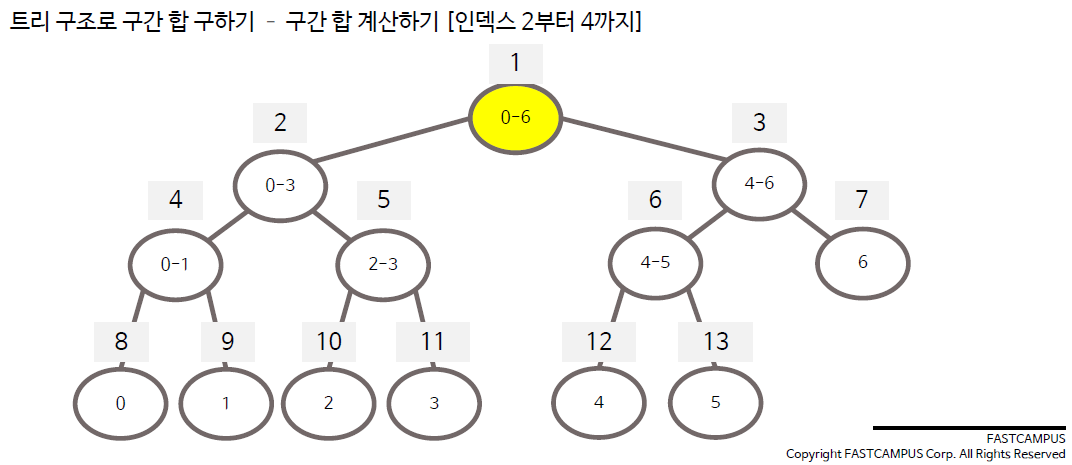
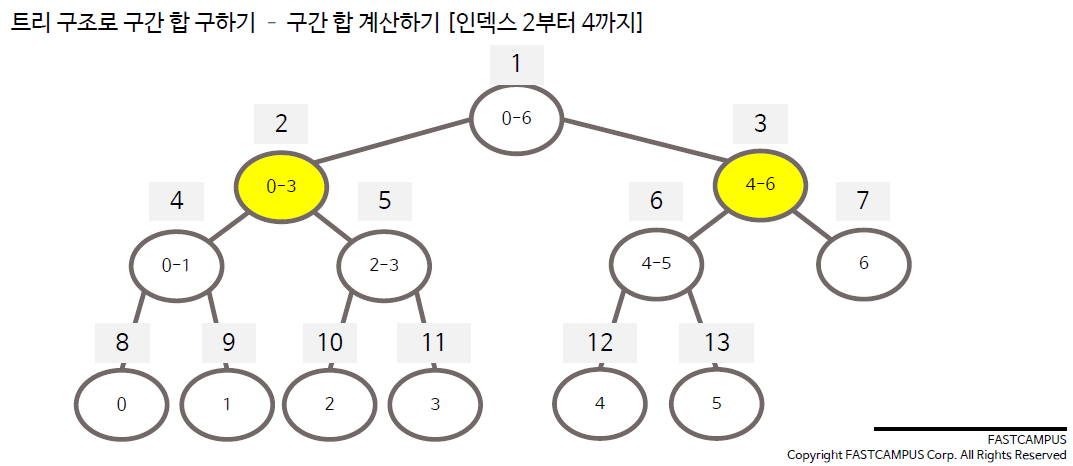
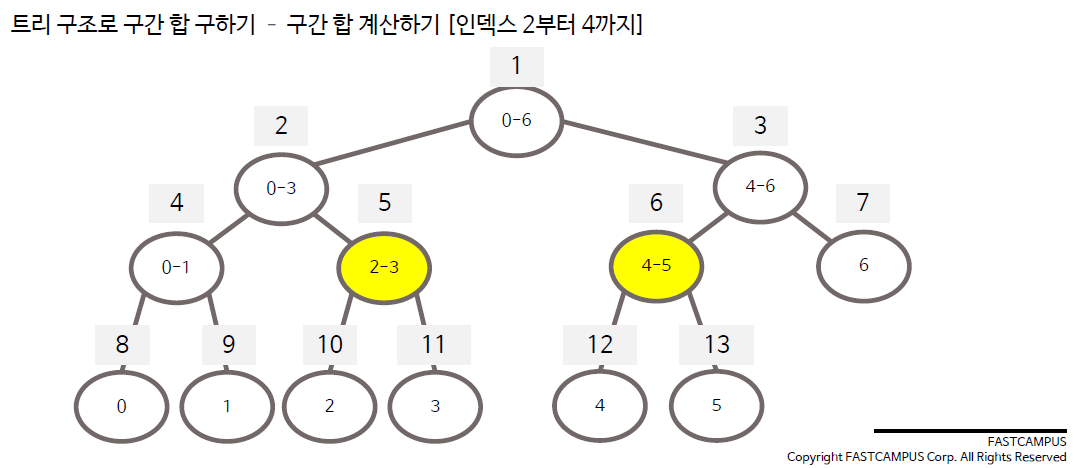
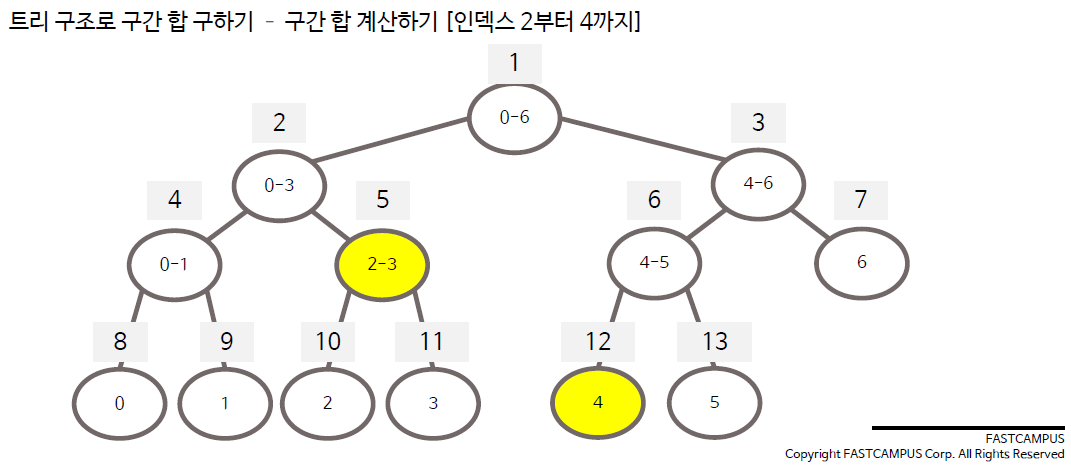
구간합 수정 방법

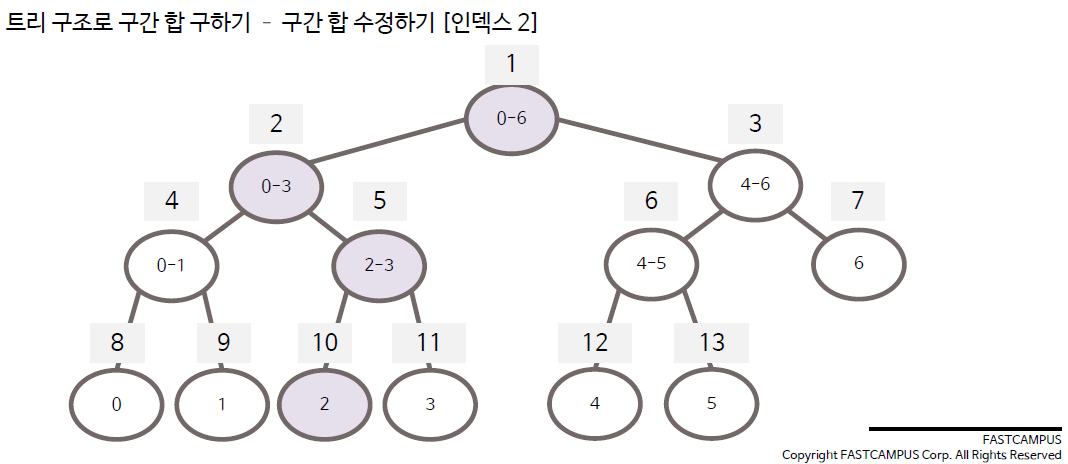
구간합 구현

#include <stdio.h>
#define NUMBER 7

// 트리 구조로 구간 합 구하기
int a[] = { 7, 1, 9, 5, 6, 4, 1 };
int tree[4 * NUMBER]; // 4를 곱하면 모든 범위 커버 가능

// start : 시작 인덱스 end : 끝 인덱스
int init(int start, int end, int node) {
    if (start == end) return tree[node] = a[start];
    int mid = (start + end) / 2;
    // 재귀적으로 두 부분으로 나눈 뒤에 그 합을 자기 자신으로 함
    return tree[node] = init(start, mid, node * 2) + init(mid + 1, end, node * 2 + 1);
}

// 구간합 계산
// left, right : 구간 합을 구하고자 하는 범위
int sum(int start, int end, int node, int left, int right) {
    // 범위 밖인 경우
    if (left > end || right < start) return 0;
    // 범위 안인 경우
    if (left <= start && end <= right)return tree[node];
    // 나머지는 두 부분으로 나누어 합 구하기
    int mid = (start + end) / 2;
    return sum(start, mid, node * 2, left, right) + sum(mid + 1, end, node * 2 + 1, left, right);
}

// 구간합 수정
// index : 수정하는 인덱스 dif : 수정할 값
void update(int start, int end, int node, int index, int dif) {
    // 범위 밖인 경우
    if (index < start || index > end) return;

    // 범위 안이면 내려가며 다른 원소도 갱신
    tree[node] += dif;
    if (start == end) return;
    
    int mid = (start + end) / 2;
    update(start, mid, node * 2, index, dif);
    update(mid + 1, end, node * 2 + 1, index, dif);
}

// main
int main(void) {
    // 구간합 트리의 인덱스를 제외하고 모두 인덱스 0부터 시작
    // 구간합 트리 생성
    init(0, NUMBER - 1, 1);

    // 구간합 구하기
    printf("0부터 6까지 구간 합 : %d\n", sum(0, NUMBER - 1, 1, 0, 6));

    // 구간합 갱신
    printf("인덱스 5의 원소를 +3만큼 수정\n");
    update(0, NUMBER - 1, 1, 5, 3);

    // 구간합 갱신
    printf("3부터 6까지 구간 합 : %d\n", sum(0, NUMBER - 1, 1, 3, 6));

    system("pause");
    return 0;
}