08. 그래프의 개념과 구현

그래프의 개념

• Graph란 사물을 정점(Vertex)와 간선(Edge)로 나타내기 위한 도구
• 두가지 방식으로 구현
  - 인접 행렬(Adjacency Matrix) : 2차원 배열을 사용
  • 인접 리스트(Adjacency List) : 리스트를 사용

인접 행렬

• 각 노드를 정점으로 보고 그 사이 연결을 간선으로 나타냄
• 각 인덱스가 정점의 순서이며 간선이 있을 경우 해당하는 숫자를 채우며 없을 경우 무한으로 표기
  ex) 0번 정점에서 1번 정점 --> [0][1] = 3
  ex) 2번 정점에서 0번 정점 --> [2][0] = 7
  ex) 1번 정점에서 2번 정점 --> [1][2] = 무한

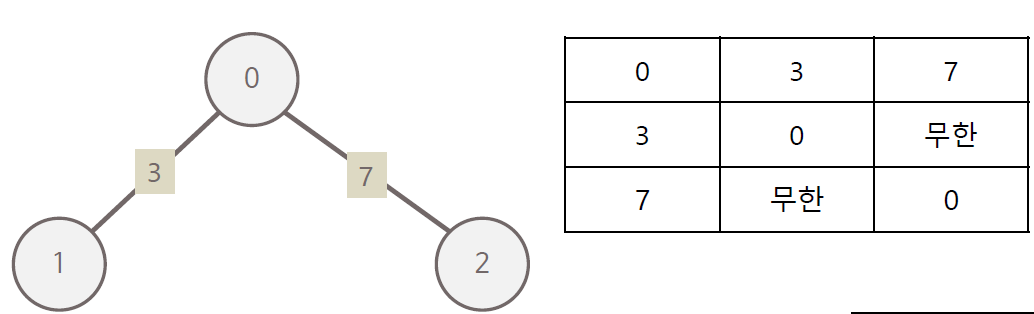
무방향 비가중치 그래프와 인접 행렬

• 모든 간선이 방향성이 없을 때의 그래프가 무방향 그래프
• 모든 간선에 가중치가 없는 그래프가 비가중치 그래프
• 무방향 비가중치 그래프가 주어졌을 때 연결되어 있는 상황을 인접 행렬로 출력 가능

무방향 비가중치 그래프와 인접 행렬 구현

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>

int a[1001][1001];
int n, m;

int main(void) {
	scanf("%d %d", &n, &m);
	for (int i = 0;i < m;i++) {
		int x, y;
		scanf("%d %d", &x, &y);
		a[x][y] = 1;
		a[y][x] = 1;
	}

	for (int i = 1;i <= n;i++) {
		for (int j = 1;j <= n;j++) {
			printf("%d ", a[i][j]);
		}
		printf("\n");
	}
	system("pause");
	return 0;
}

방향 가중치 그래프와 인접 리스트

• 모든 간선이 방향을 가지는 그래프가 방향 그래프
• 모든 간선에 가중치 있는 그래프가 가중치 그래프
• 방향 가중치 그래프가 주어졌을 때 연결되어 있는 상황을 인접 리스트로 출력 가능

방향 가중치 그래프와 인접 리스트 구현

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

// 노드(정점) 구조체 선언
typedef struct {
	int index;
	int distance;
	struct Node* next;
} Node;

// 연결리스트의 삽입
void addFront(Node* root, int index, int distance) {
	Node* node = (Node*)malloc(sizeof(Node));
	node->index = index;
	node->distance = distance;
	node->next = root->next;
	root->next = node;
}

// 리스트 모든 원소 출력
void showAll(Node* root) {
	Node* cur = root->next;
	while (cur != NULL) {
		printf("%d (거리 : %d) ", cur->index, cur->distance);
		cur = cur->next;
	}
}

int main(void) {
	int n, m;
	scanf("%d %d", &n, &m); // n개의 정점과 m개의 간선
	Node** a = (Node**)malloc(sizeof(Node*) * (n + 1)); // 2차원

	for (int i = 1;i <= n;i++) {
		a[i] = (Node*)malloc(sizeof(Node));
		a[i]->next = NULL;
	}
	// 정점1과 정점2, 거리를 받아 삽입
	for (int i = 0;i < m;i++) {
		int x, y, distance;
		scanf("%d %d %d", &x, &y, &distance);
		addFront(a[x], y, distance);
	}
	
	for (int i = 1;i <= n;i++) {
		printf("원소 [%d] : ", i);
		showAll(a[i]);
		printf("\n");
	}
	system("pause");
	return 0;
}

정리

• 인접 행렬은 모든 정점들의 연결 여부를 저장하여 O(V^2)의 공간을 요구하므로 공간 효율성이 떨어지지만 두 정점이 서로 연결되어 있는지 확인하기 위해 O(1)의 시간을 요구
• 인접 리스트는 연결된 간선의 정보만을 저장하여 O(E)의 공간을 요구하므로 공간 효율성이 우수하지만 두 정점이 서로 연결되어 있는지 확인하기 위해 O(V)의 시간을 요구