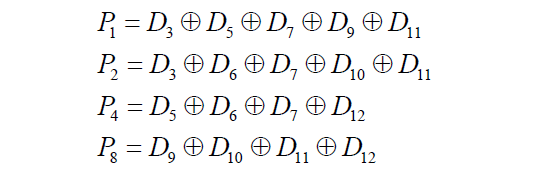05. 데이터의 종류

컴퓨터에서의 데이터 표현

컴퓨터에서의 데이터 표현은 다음과 같이 5가지로 추려볼 수 있다.

• 진법/진법 변환
• 정수 표현
• 실수 표현
• 디지털 코드
• 에러 검출 코드

진법/진법 변환

진법

디지털 정보의 단위로 많이 활용되는 것은 1byte이며 8bit로 환산된다. 영어는 1byte로 1문자를 표현하며 한글은 2byte가 필요하다.

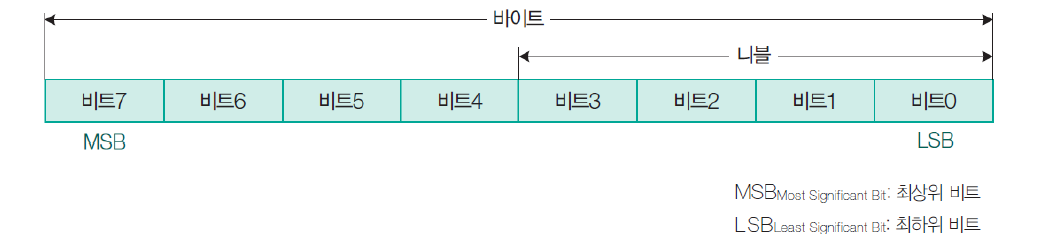
컴퓨터는 on/off로 표기할 수 있는 2진법체계를 택하는데 이를 더 효율적으로 표현하고자 8진법, 16진법도 사용을 한다.

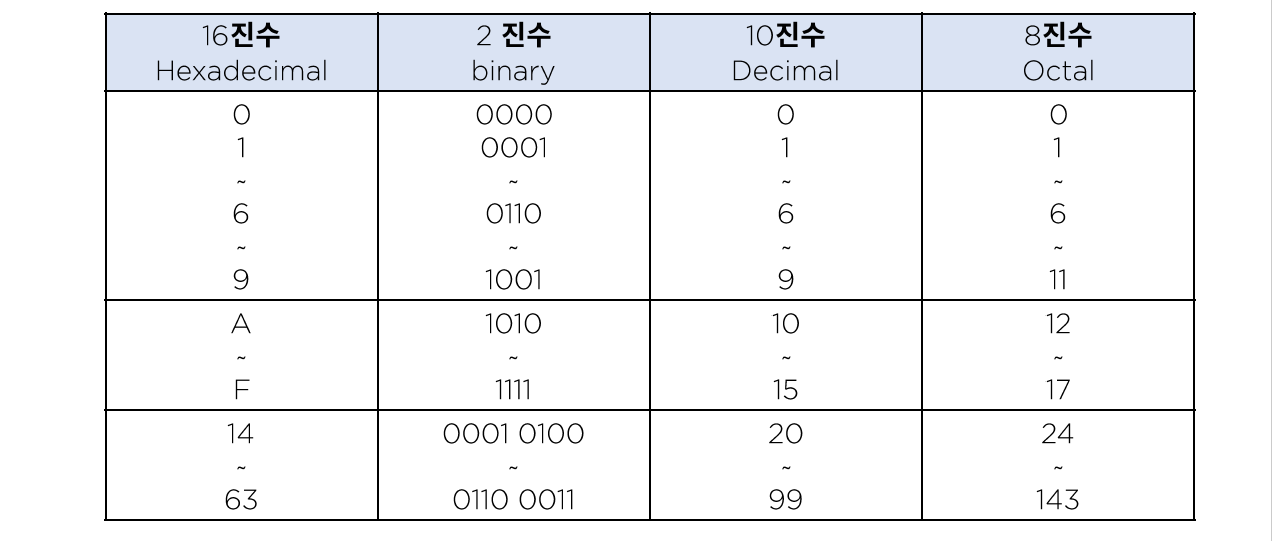
진법 변환

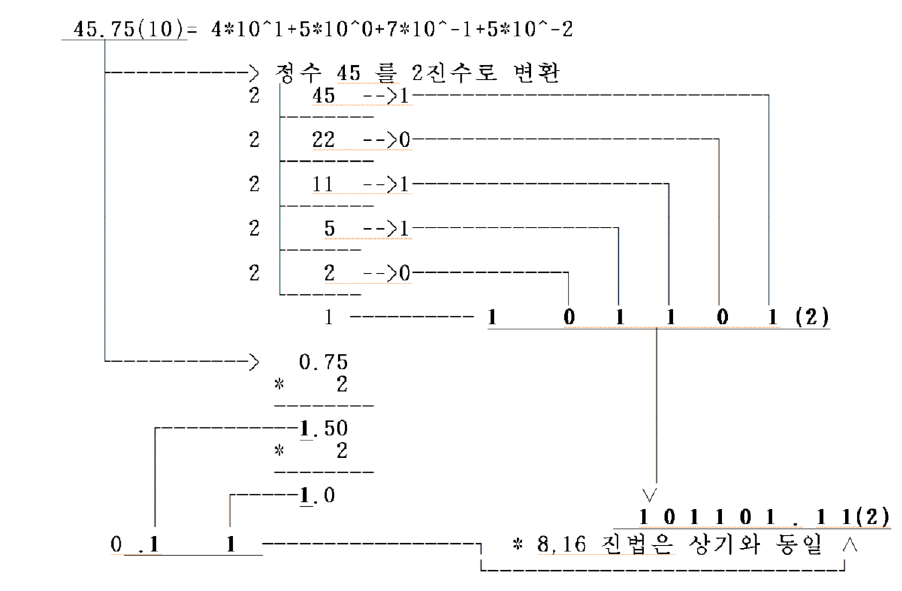
기본적으로 10진법의 수를 2진법으로 변환할 때에는 다음과 같은 방법으로 나눗셈을 한 나머지를 차용하여 표기한다.

2진수를 10진수로 표기할 때 수식으로는 다음과 같이 표기할 수 있다.

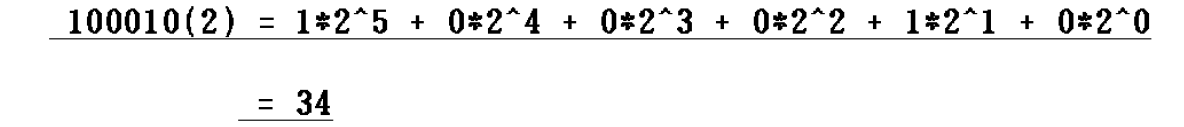
또한 8/16진수는 2진수의 배수이기에 변환이 용이하다.

실수를 변환할 때에는 소수점 아래의 값들을 2씩 곱하여 나오는 몫을 차용하여 표기한다.

보수

이제 컴퓨터 데이터 연산의 가장 중요한 근간이 되는 보수개념이 등장한다.

• one's complement : 최대값(해당 bit의 가장 큰 표현형)을 형성하는데 서로 보완 관계에 있는 두 수 사이의 관계
• two's complement : 최대표현자리수(modulus)를 형성하는데 보완관계에 있는 두 수 사이의 관계

ex) 10진수
1의 보수 : A+B=9, A+B=99
2의 보수 : A+B=10, A+B=100

ex) 2진수
1의 보수 : A+B=1, A+B=11
2의 보수 : A+B=10, A+B=100

2진수의 1의 보수는 자신의 수를 반대(1↔0)로 취하고 2의 보수는 1의 보수에 1을 더한다.

정수 표현

정수의 부호와 절대치를 따로 보관하며 MSB가 부호가 된다.

이 때 1의 보수와 2의 보수의 표현범위가 다르다.

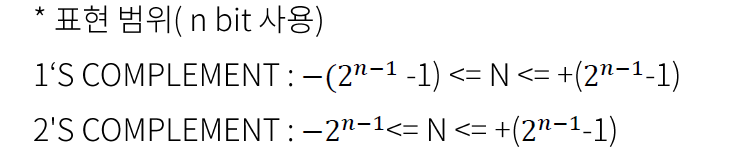
Unpacked/Packed decimal

unpacked decimal은 1byte로 10진수 한자리만 표현하며 연산에는 이용 될 수 없으나 입출력이 가능하다. 여러 자리수의 숫자를 표현할 때 모든 byte들은 full digit으로 표현되나 마지막 byte만 sign을 포함한다.

packed decimal은 1byte에 2자리의 10진수를 표현하며 마지막 4개의 비트로 부호를 표현한다. 연산에 이용되고 입출력이 불가하다.

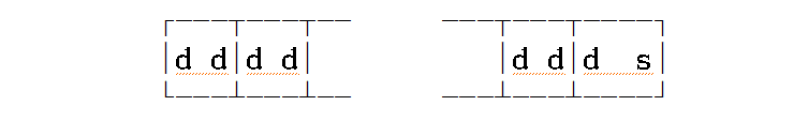
실수 표현

지수와 기수를 사용하여 소수점의 위치를 이동시켜 표기할 수 있는 표현 방법이며 표현의 범위가 정수에 비해 훨씬 넓다. 1bit는 부호, 다음 7bit는 지수, 다음 24bit는 기수를 표현한다.

만약 다음과 같은 예시가 있다면

양의 부호를 가지며 10진수로 5의 지수를 가지고 0.9의 기수를 가지기 때문에 0.9x10^5의 값을 표현한 것이다.

디지털 코드

위에서 언급한 packed decimal 표기시 BCD code를 사용하는데 이는 다음과 같다.

에러 검출 코드

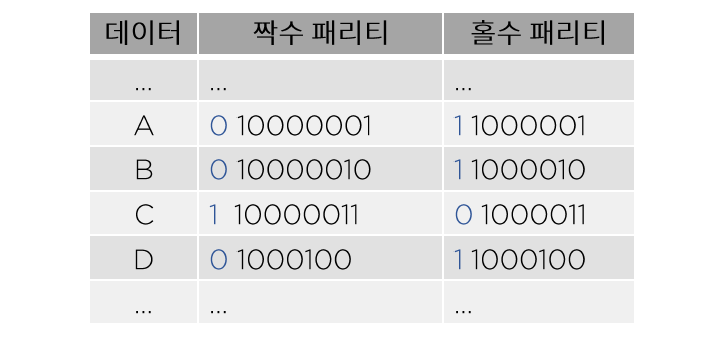
패리티 비트라 하여 데이터의 진위여부를 검사하는 것인데 다음과 같이 짝수 패리티 혹은 홀수 패리티로 검사한다. 해당 데이터의 1의 개수가 짝수이면 최상단에 0을 홀수이면 1을 삽입하여 총 1의 개수를 짝수를 맞추는 것이 짝수 패리티이다.

해밍 비트라하여 8비트 데이터의 에러 정정 코드도 있는데 다음과 같이 표기를 한다.