https://www.acmicpc.net/problem/1022

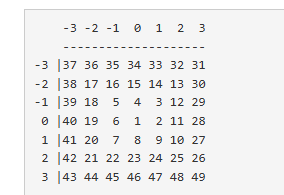
이런모양으로 확장되는 모눈종이의 일부를 출력하는 문제이다

Python

1차 시도 - 메모리 초과

r1, c1, r2, c2 = map(int, input().split())

n = max(abs(r1), abs(c1), abs(r2), abs(c2))

# 전체 모눈종이의 너비 혹은 소용돌이의 너비
n = 2 * n + 1

def makeCyclone(n):
    sy, sx = n//2, n//2

    cycle = [[0] * n for _ in range(n)]
    cycle[sy][sx] = 1

    dx = [1, 0, -1, 0]
    dy = [0, -1, 0, 1]

    d = 0
    l = 1
    number = 2

    while sy < n and sx < n:
        for i in range(l):
            sy = sy + dy[d]
            sx = sx + dx[d]

            if sy >= n or sx >= n:
                break

            cycle[sy][sx] = number
            number += 1
        d = (d + 1) % 4
        if d == 0 or d == 2:
            l += 1

    return cycle

cycle = makeCyclone(n)

r1 += n//2
r2 += n//2
c1 += n//2
c2 += n//2

for i in range(r1, r2+1):
    row = cycle[i]
    print(' '.join(map(str,row[c1:c2+1])))

입력되는 값 중 최대값을 가지고 필요한 전체 모눈종이의 너비를 구한 후, makeCyclone 함수를 통해서 모눈종이를 그렸다.
그리고 일부를 출력했는데 아무래도 5000 * 5000 크기의 모눈종이를 그리게 될 경우에 메모리에 담기에는 너무 컸나보다.

수학적으로 접근할 필요가 있겠다.

시도 2 - 출력 형식 실패

r1, c1, r2, c2 = map(int, input().split())

n = max(abs(r1), abs(c1), abs(r2), abs(c2))

def cal_start(n):
    if n == 0:
        return 1
    return 4 * n * (n - 1) + 2

def cal_number(i, j):
    n = max(abs(i), abs(j))
    start_num = cal_start(n)
    if n == 0:
        return 1
    sy, sx = n-1, n

    dy = [-1, 0, 1, 0]
    dx = [0, -1, 0, 1]

    d = 0

    turningPoint = {(-n, n), (-n, -n), (n, -n)}

    while (dy, dx) != (n, n+1):
        if sy == i and sx == j:
            return start_num

        if (sy, sx) in turningPoint:
            d = (d+1)%4

        sy += dy[d]
        sx += dx[d]
        start_num += 1



ans = [[0] * (c2 - c1 + 1) for _ in range(r2 - r1 + 1)]

for i in range(r1, r2+1):
    for j in range(c1, c2+1):
        ans[abs(i - r1)][abs(j - c1)] = cal_number(i, j)

if len(ans) == 1 and ans[0][0] // 10 == 0:
    print(ans[0][0])
else:
    for a in ans:
        tmp = ""
        for c in a:
            if c//10 == 0:
                tmp += " " + str(c)
            else:
                tmp += str(c)
            tmp += " "

        print(tmp)

네모의 길이 규칙을 먼저 찾아보았다

0 1 2 3 4
1, 3+3+1+1, 5+5+3+3, 7+7+5+5, 9+9+7+7
1, 8 , 16 , 24 , 32

그리고 다음과 같은 수열의 공식을 얻었고

n번째 네모
x(n) = 2 * (2n-1 + 2n+1) = 8n

n번째 네모의 끝점: 4 (n+1) n + 1
0: 0 + 1 = 1
1: 4 2 1 + 1 = 9
2: 4 3 2 + 1 = 25
3: 4 4 3 + 1 = 48 + 1 = 49

네모의 끝점을 얻었으니 n번째 네모의 시작점의 숫자는 4 n (n-1) + 2가 되는 것을 알 수 있다.

또한, 점이 (i, j)일 때 네모는 max(abs(i), abs(j))을 통해서 몇 번째 네모인지 구할 수 있다.

시작점부터 탐색하기로 결정했다. 탐색했을 때 최악의 경우는 해봐야 49 4 (5000 * 4)일 것이라 판단돼서 아까 2천5백만의 메모리보다는 나을 것 같았다.

turningpoint를 만들어서 여기에 도착할 때마다 방향을 전환하도록 했으며, 탐색 도중 원한는 위치를 찾는다면 해당 위치의 숫자를 반환하도록 했다.

그리고 출력했는데 출력 모양에서 실패했다.

예쁜 모양이라는게 자리 위치까지 맞추라는 것인 줄은 몰랐다.

시도 3

r1, c1, r2, c2 = map(int, input().split())

n = max(abs(r1), abs(c1), abs(r2), abs(c2))

def cal_start(n):
    if n == 0:
        return 1
    return 4 * n * (n - 1) + 2

def cal_number(i, j):
    n = max(abs(i), abs(j))
    start_num = cal_start(n)
    if n == 0:
        return 1
    sy, sx = n-1, n

    dy = [-1, 0, 1, 0]
    dx = [0, -1, 0, 1]

    d = 0

    turningPoint = {(-n, n), (-n, -n), (n, -n)}

    while (dy, dx) != (n, n+1):
        if sy == i and sx == j:
            return start_num

        if (sy, sx) in turningPoint:
            d = (d+1)%4

        sy += dy[d]
        sx += dx[d]
        start_num += 1



ans = [[0] * (c2 - c1 + 1) for _ in range(r2 - r1 + 1)]
maxLen = 0
for i in range(r1, r2+1):
    for j in range(c1, c2+1):
        ans[abs(i - r1)][abs(j - c1)] = cal_number(i, j)
        maxLen = max(len(str(ans[abs(i - r1)][abs(j - c1)])), maxLen)

for line in ans:
    tmp = ""
    for l in line:
        for _ in range(maxLen - len(str(l))):
            tmp += " "
        tmp += str(l) + " "
    print(tmp[:-1])

숫자를 찾으면서 maxLen이라는 변수에 최대 자리수를 저장하였다. 그리고 출력하면서 maxLen에 부족한 만큼 공백을 추가하였고 tmp가 완성됐을 때 출력은 마지막 공백을 제거하여 출력하였다.