https://www.acmicpc.net/problem/2437

양팔저울이 있고, 추가 여러개 있을 때 추를 조합해서 만들 수 없는 가장 작은 정수를 찾는 문제이다.

조합으로 접근할지, BFS로 접근할지 고민하다가 답이 안나와서 질문하기를 참고했다.

https://www.acmicpc.net/board/view/45841

여기서 첫번째부터 i번째 추까지의 합인 sum까지는 i개의 추의 조합으로 만들수 있다고 가정했을 때, i+1번째 추의 무게가 sum+1보다 크다면 만들 수 없는 가장 작은 정수는 sum+1이 된다고 설명한다.

여기서 결론은 sum+1보다 i+1번째 추의 무게가 더 크다면 sum+1부터 sum + w[i+1]-1까지의 간격이 생기기에 만들 수 없는 정수가 생긴다는 것은 이해했다.

반대로 i+1번째 추의 무게가 sum+1 이하라면 sum[i+1]까지의 정수를 만들 수 있다는 소리인데, 이 부분은 이해가 안 간다.

최초에 sum을 0으로 두고, 첫 숫자가 2라면 sum+1 < 2이기에 안 되고, 대신 1이라면 sum+1 == 1이라서 1까지는 가능.
sum이 1이고 그 다음 숫자가 3이라면 sum + 1 == 2 < 3이라서 간격 2가 생겨서 조합 불가능이고, 2라면 가능.
sum이 1+2이고 다음 숫자가 5라면 sum+1 == 4 < 5라서 간격 4가 생겨서조합 불가능이고 4라면 가능
sum이 1+2+4이고, 다음 숫자가 9라면 sum+1 == 8 < 9라서 간격 8이 생겨서 조합 불가능, 8까지 가능

뭐 이런식인데, 1, 2까지는 이해가 가는데 1,2,4가 된 순간부터 3이 없는데 어떻게 조합이 가능한거지 싶어서 잘 모르겠다.

GPT한테 물어보고 생각을 했는데, 만약 w[i+1]이 sum[i]보다 작거나 같을 때 sum[i] + w[i+1]까지 가능한 이유는
w[i+1]을 시작으로 sum[i]만큼의 조합을 더할 수 있어서 그렇다고 한다.

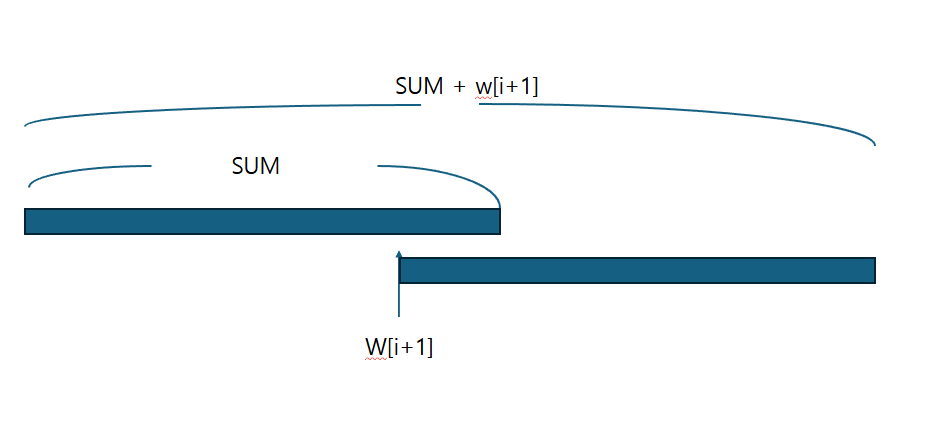
이런느낌인 것 같다. 숫자로만 봐서 이해 안 됐는데 그림 그려보니까 이해가 됐다.
그래서 이런 원리로 귀납적으로 1부터 시작해서 적용이 되는 것 같다.

Python

n = int(input())
sum = 0
for w in sorted(list(map(int, input().split()))):
    if sum + 1 >= w:
        sum += w
    else:
        break
print(sum+1)