[Leetcode] K-th Smallest Prime Fraction

https://leetcode.com/problems/k-th-smallest-prime-fraction/description/

정렬된 소수 배열을 주고 해당 숫자로 분수를 만드는데 기약분수만 뽑아내서 k번째 작은 분수를 찾고 해당 분자와 분모를 배열로 반환하는 문제이다.

시도 1 - 2중 for문

배열의 크기가 1,000이라서 n^2해도 최대 백만이겠다 싶어서 일단 이중 for문으로 처리하고 풀었다.

class Solution:
    def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:
        fractions = [[0] * len(arr) for _ in range(len(arr))]
        results = set()

        for i in range(len(arr)):
            for j in range(i+1, len(arr)):
                fractions[i][j] = arr[i] / arr[j]
                results.add(arr[i] / arr[j])
        
        results = list(results)
        results.sort()

        ans = results[k-1]
        print(ans)

        for i in range(len(arr)):
            for j in range(i+1, len(arr)):
                if fractions[i][j] == ans:
                    return [arr[i], arr[j]]        

배열의 index로 2차원 배열을 만들고 거기에 나눗셈한 결과를 넣었다. 물론 분자가 분모가 작은 경우에만 계산이 되도록 했다. 그리고 정렬을 하였고 2차원 배열을 돌면서 k번째 분수 즉 소수가 어디있는지 찾아서 그 결과를 반환했다.

그리고 문제 마지막에

이런 조건이 달려있었다.

시도 2 - 집합

해당 조건을 만족시키기 위해서 다른 접근 방식을 사용해봤다.

class Solution:
    def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:
        fractions = []

        for i in range(len(arr)):
            for j in range(i+1, len(arr)):
                fractions.append((arr[i] / arr[j], [arr[i], arr[j]]))
        
        record = set()

        fractions.sort()
        count = 0
        for f in fractions:
            if f[0] not in record:
                if count == k - 1:
                    return f[1]
                
                record.add(f[0])
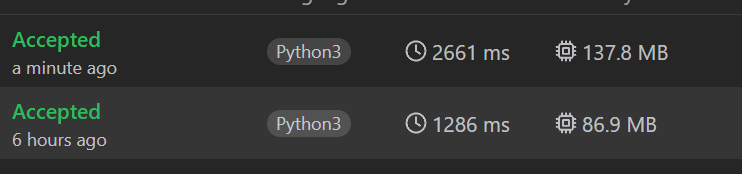
                count += 1

나눗셈의 결과와 분자와 분모를 함께 저장한 튜플을 담을 리스트를 만들고 정렬했다. 그리고 앞에서부터 돌면서 k번째 작은 소수를 찾는데 중복값을 제거하기 위해서 record라는 집합을 만들어서 돌면서 나온 소수를 저장해서 중복값을 걸러냈다. 그런데 이렇게 하니까 첫번째 코드보다 시간이 두 배 정도 느리게 나왔다.

시도 3 - 힙

챗지피티 선생님이 힙을 사용해보라고 해서 힙으로 접근해봤다.

from heapq import heappush, heappop

class Solution:
    def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:
        fractions = []

        for i in range(len(arr)):
            for j in range(i+1, len(arr)):
                heappush(fractions, (arr[i] / arr[j], [arr[i], arr[j]]))
        
        record = set()

        fractions.sort()
        count = 0
        while fractions:
            f = heappop(fractions)
            if f[0] not in record:
                if count == k - 1:
                    return f[1]
                
                record.add(f[0])
                count += 1
                

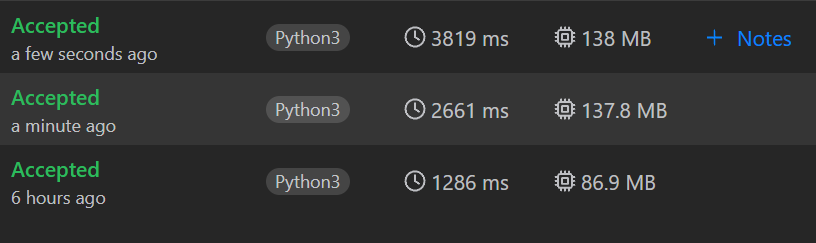
왜지...... 더 느리게 나왔다. 메모리도 더 사용했고, set이 접근 시간이 O(1)이라고 하던데 힙 연산이 더 오래걸렸나 싶다. 아 어쨌든 2중 for문이라서 그런거 같기도 하다.

시도 4 - GPT가 알려준 코드

import heapq

class Solution:
    def kthSmallestPrimeFraction(self, arr, k):
        n = len(arr)
        # Min-heap to store fractions with their indices
        heap = []
        
        # Push initial fractions (arr[0] / arr[j]) into the heap
        for j in range(1, n):
            heapq.heappush(heap, (arr[0] / arr[j], 0, j))
        
        # Extract the smallest fraction k times
        for _ in range(k - 1):
            frac, i, j = heapq.heappop(heap)
            # If there is a next fraction in the same row (i), push it to the heap
            if i + 1 < j:
                heapq.heappush(heap, (arr[i + 1] / arr[j], i + 1, j))
        
        # The k-th smallest fraction
        _, i, j = heapq.heappop(heap)
        return [arr[i], arr[j]]

똑같이 힙을 사용했는데 이 코드는 더 효율이 좋게 나왔다.
접근 방식은 가장 작은 분수들인 분자가 1인 분수를 먼저 넣는 것으로 시작했다. 그리고 k-1번 돌면서 해당 분수를 꺼내고, 분자가 1 다음으로 큰 분수를 넣고 하는 식으로 접근을 했다. 이렇게 되면 해봐야 O(n+k)만큼의 연산이라서 더 빠르게 연산이 된 것 같다.

해결하긴 했으나 더 효율적인 방법을 찾지 못했기에 나중에 다시 풀어봐야겠다.