https://school.programmers.co.kr/learn/courses/30/lessons/258705?language=java

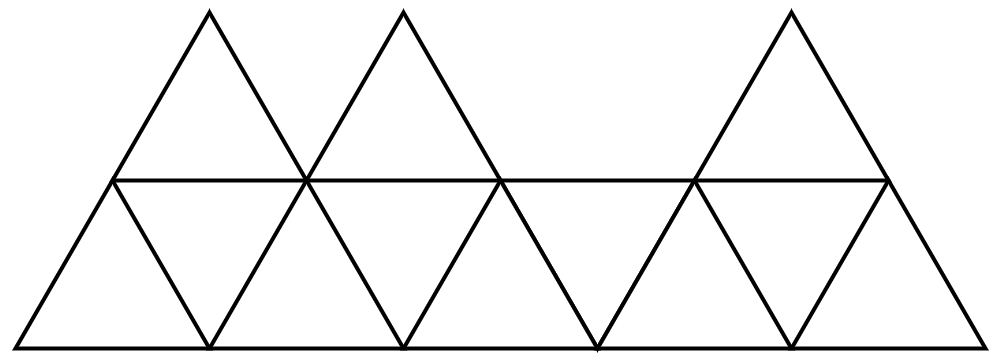
이렇게 생긴 타일에 마름모와 정삼각형을 적절히 배치해서 채울 때 나올 수 있는 경우의 수를 구하는 문제이다.

아래 라인의 정삼각형들은 무조건 있고, 제일 위쪽 라인은 삼각형이 있을 수도 있고 없을 수도 있다.

Python

def solution(n, tops):
    upper = set()
    for idx, t in enumerate(tops):
        if t:
            upper.add((idx + 1) * 2 - 1)

    dp = [0] * (2 * n + 1)
    dp[0] = 1
    dp[1] = 3 if 1 in upper else 2

    for x in range(2, 2 * n + 1):
        dp[x] = (dp[x - 1] + dp[x - 2] + (dp[x - 1] if x in upper else 0)) % 10007

    return dp[-1] % 10007

dp를 먼저 2n+1만큼 선언하였다. 아래 라인의 삼각형들의 총 개수가 2n+1이기 때문이다.
그리고 tops에 있는 숫자를 반영했는데, 아래 라인에서 뒤집한 삼각형의 index는 1, 3, 5, 7 ... 2n-1 이렇게 홀수로 진행되기 때문에 upper에는 2(i+1)-1을 넣어주었다.

그리고 일단 아래 라인 삼각형만 있는 경우의 점화식을 세웠는데 다음과 같다.

dp[n] = dp[n-1] + dp[n-2]

n번째 n-1까지 채워지고 n번째는 정삼각형인 경우 + n-2까지 채워지고 n-1과 n이 마름모인 경우이다.

여기에 더해 n번째 삼각형의 위에 삼각형이 있는 경우에는 그냥 삼각형인 경우와 경우의 수가 같기에 dp[n-1]을 한 번 더해주었다.

dp[n] = dp[n-1] + dp[n-2] + ( dp[n-1] if n in upper else 0 )

그리고 dp[0]은 1로, dp[1]은 2로 초기화를 했는데, 첫번째 역삼각형 위에 다른 삼각형이 있는 경우에는 1을 추가로 더해서 3으로 초기화 하였다.

Java

class Solution {
    public int solution(int n, int[] tops) {
        int[] dp = new int[2 * n + 1];
        int[] upper = new int[2 * n + 1];

        for (int i = 0; i < 2 * n + 1; i++) {
            dp[i] = 0;
            upper[i] = 0;
        }

        for (int i = 0; i < tops.length; i++) {
            if (tops[i] == 1) {
                upper[2 * (i + 1) - 1] = 1;
            }
        }

        dp[0] = 1;
        dp[1] = upper[1] == 1 ? 3 : 2;

        for (int i = 2; i < 2 * n + 1; i++) {
            dp[i] = (dp[i - 1] + dp[i - 2] + (upper[i] == 1 ? dp[i - 1] : 0)) % 10007;
        }

        return dp[2 * n] % 10007;
    }
}

HashSet을 사용하려 했지만 자바에서 HashSet에 접근할 때 시간이 O(1)인지 아닌지 확신이 없어서 그냥 dp와 같은 사이즈의 배열을 만들고, tops에 있는 삼각형에 대해서만 1을 넣어주었다.