
빅오 표기법
빅오 표기법이란 ?

빅오 표기법이란
빅오 표기법은 점근 표기법 중 가장 많이 사용되는 표기법인데 알고리즘의 효율성을 분석 할 때 사용한다.
먼저 그래프를 살펴보자.
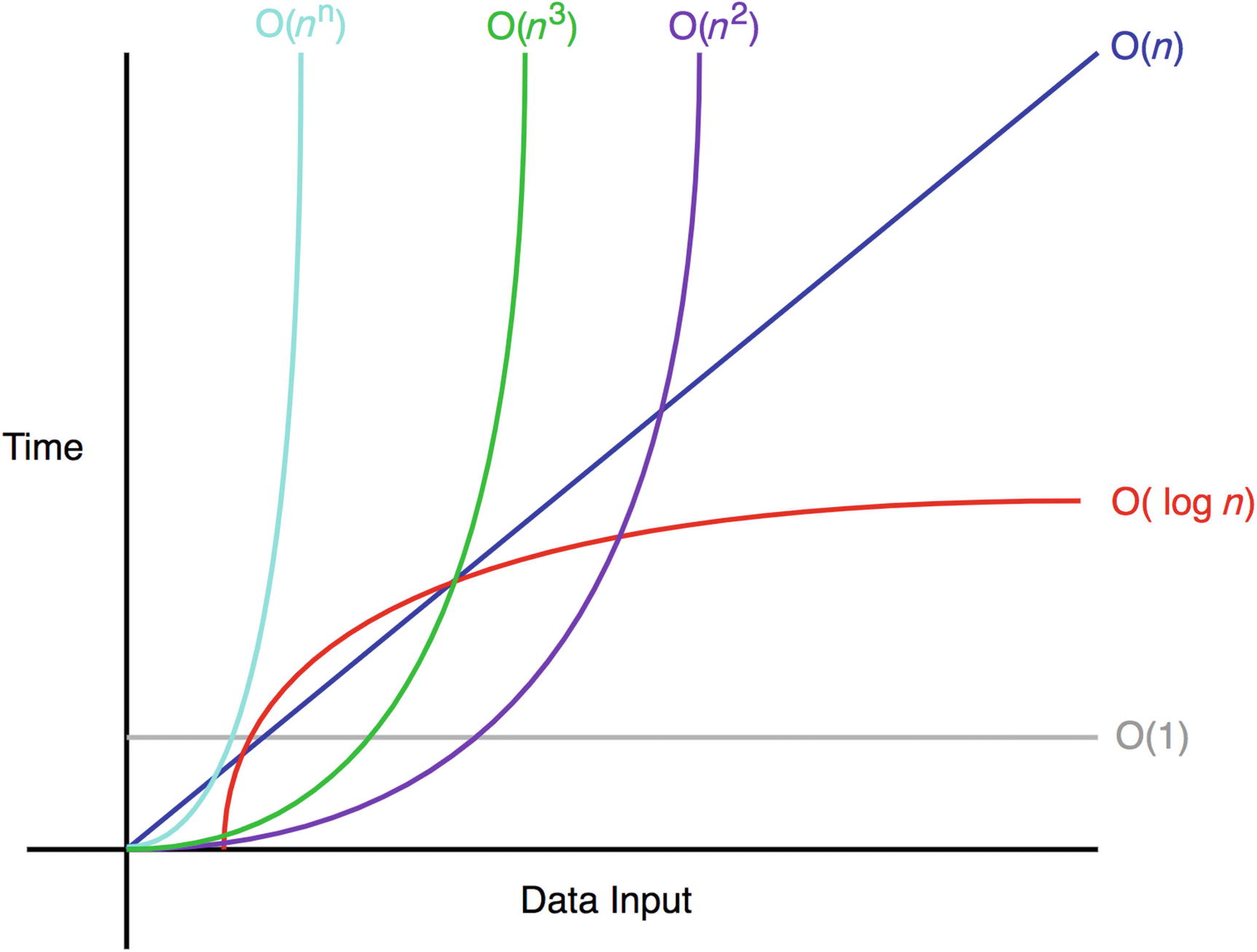
여러가지 빅오들(?)
빅오 표기법은 그래프와 같이 계수 항과 차수 항에 따라 효율이 달라진다.
-
O(1) : 입력 데이터의 크기에 상관없이 언제나 동일한 시간이 걸리는 알고리즘.
-
O(log n) : 입력 데이터의 크기가 커질 수록 처리 시간이 로그만큼 짧아지는 알고리즘
-
O(n) : 입력 데이터의 크기에 비례하여 처리 시간이 증가하는 알고리즘
-
O(n^2) : 데이터가 많아질 수록 처리시간이 급수적으로 늘어나는 알고리즘
-
O(2^n) : 데이터량이 많아질 수록 처리시간이 기하급수적으로 늘어나는 알고리즘
그래프를 보시다시피 Data의 양이 많아 질수록 Time이 높이 올라가는 녀석들은 비효율적이며 Time이 낮은 친구들이 효율적이다.
빅오는 어떻게 계산하지 ?

계산을 하기 전 우리는 시간복잡도와 공간 복잡도에 대해 알아야한다.
- 시간 복잡도
알고리즘의 수행 시간을 평가
- 공간 복잡도
알고리즘 수행에 필요한 메모리 양을 평가
시간 복잡도는 데이터 입출력, 사칙/산술 연산, 제어 연산들이 영향을 미친다.
공간 복잡도는 변수, 자료구조, 함수 호출, 할당들이 영향을 미친다.
시간 복잡도
O(1)
const test = [1,2,3];
console.log(test[0]); // O(1)
console.log(test[1]); // O(1)test 배열의 길이와 상관 없이 일정한 시간이 걸린다.
O(n)
const test = [1,2,3,4,5];
for(let i = 0; i < test.length; i++){
console.log(i);
}
// O(n)test 배열의 길이가 길 수록 반복문은 n번 동작한다.
O(n^2)
const test = [1,2,3,4,5];
for(let i = 0; i < test.length; i++){
for(let j = 0; j < test.length; j++){
console.log(i, j);
}
}
// O(n^2)반복문 안에 또 다른 반복문을 사용하면 test 배열의 n의 제곱 만큼 동작하게 된다.
O(2^n)
function fibonacci(num){
if(num <= 0){
return 0;
}
else if(num === 1){
return 1
}
else {
return fibonacci(num-1) +fibonacci(num-2)
}
}
가장 유명한 피보나치 수열을 예로 들면 2의 n 제곱만큼 데이터양이 늘어나는데 이는 함수 호출 시 함수가 두 번씩 호출 되기 때문이다.
O(log n)
const arr = [1, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59];
const binarySearch = (sortedArray, value) => {
let min = 0;
let max = sortedArray.length - 1;
while (min <= max) {
let mid = Math.floor((min + max) / 2);
let currentElement = sortedArray[mid];
if (currentElement < value) {
min = mid + 1;
} else if (currentElement > value) {
max = mid - 1;
} else {
return mid;
}
}
return -1;
};
console.log(binarySearch(arr, 37)); // 11대표적으로 이진 탐색법이 log n의 시간 복잡도를 가지고 있다.
시간복잡도 계산 규칙
빅오는 4가지의 규칙을 가지고 있다
- 최악의 상황을 고려하라 !
const arr = [1, 2, 3, 4, 5];
for(let i = 0; i < arr.length; i++){
if(i === 1){ // 1이 아니라 5라면 ??
console.log("찾았다 !");
break;
}
}위의 코드에 있어 1을 찾는데 걸리는 시간 복잡도는 O(1)이다 .
하지만 1이 아닌 n의 숫자가 들어간다면 O(n)이 된다. 그러니 항상 자신의 원하는 값에 대한 시간복잡도가 아닌 최악의 상황까지 고려해야한다.
- 상수 따윈 필요 없다 !
상수 존재의 유무는 필요할 수 있겠지만 중요도는 떨어진다.
위에 나와 있는 시간복잡도 그래프를 보면 알겠지만 시간과 데이터 량이 어느 수준에선 평행에 가깝게 증가하기 때문에 상수는 크게 의미가 없다는 것이다.
- input이 다르다면 따로 계산하라 !
function test(a, b) {
for(let i = 0; i < a; i++){
console.log(a);
}
for(let j = 0; j < b; j++){
console.log(b)
}
}a와 b의 값에 따라 두 for문의 실행 횟수는 차이가 생기게 된다.
input이 다를 경우 따로 계산을 해주어야한다.
이런 경우에 Big O는 O(a+b)이다.
- 제곱 앞에 상수 (혹은 n)은 필요 없다 !
이 또한 두 번째와 같은 이야기이다.
시간 복잡도가 O(n + n^2)와 같은 형태이면 n은 n^2에 비해 시간 복잡도에 크게 중요도를 차지하지 않는다.
공간복잡도 계산
앞서 설명했듯이 공간 복잡도는 데이터가 메모리에 얼마만큼에 공간을 차지하느냐에 따라 달라진다.
function test(n) {
for(let i = 0; i < n; i++){
console.log(i);
}
}위의 코드를 살펴보면 n에 숫자 어떠한 숫자가 들어 가느냐에 따라 변수 i는 n번 선언될 것이다.
그렇기 때문에 위의 공간 복잡도는 O(n)이다.
오늘의 느낀점✍

사실 공간 복잡도가 중요한지는 아직 코린이라 잘 와닿지 않는다...
(왠지 펌웨어 쪽에서 많이 사용할 거 같은..?)
그에 반해 시간 복잡도는 최적화에 꼭 필요하다고 느꼈다.
그리고 코드를 짤 때 조금 더 시간 복잡도에 대해 생각을 하고 코드를 짜게 되었다.
웹 개발에 있어 시간의 최적화는 줄일 수 있다면 당연히 줄여야하는 것이다.
그래야 사용자가 더 빠른 웹을 이용할 수 있으니 ! (느려터진 웹 누가 씁니까 ! 예 ?!)
