1. Graph
그래프는 정점과 간선으로 이루어진 자료구조
정점(Vertex)간의 관계를 표현하는 조직도
컴퓨터 세계에서 그래프란 x과 y축으로 이루어진 그래프가 아니라 정점(vertex)과 정점들을 연결하는 간선(edge)을 하나로 모아 놓은 자료 구조이다. 정점이란 어떠한 상태 혹은 객체를 나타낸다. 간선은 그러한 정점 간의 관계, 그중에서도 연결성을 표현하는 요소이다.
정점(vertex)간의 관계를 표현하는 조직도라고 볼수도 있다. 그런면에서 트리는 그래프의 일종인 셈이다. 그래프는 객체와 이에 대한 관계를 나타내는 유연한 방식으로 이해할 수 있다.
실사용 예제
우리는 일상생활을 하면서 매일같이 자료구조 그래프를 사용하고 있다. 포털 사이트의 검색 엔진, SNS에서 사람들과의 관계, 네비게이션 (길찾기) 등에서 사용하는 자료구조가 바로 그래프이다.
ex) 네비게이션
서울에 사는 A는 부산에 사는 B와 오랜 친구 사이입니다. 이번 주말에 부산에서 열리는 B의 결혼식에 참석하기 위해 A는 차를 몰고 부산으로 가려고 합니다. 대전에 살고 있는 친구 C도 B의 결혼식에 참석을 한다고 하여, A는 서울에서 출발하여 대전에서 C를 태워 부산으로 이동을 하려고 합니다.
- 정점: 서울, 대전, 부산
- 간선: 서울—대전, 대전—부산, 부산—서울
비가중치 그래프 : 가중치(연결의 강도가 얼마나 되는지)가 적혀 있지 않은 그래프
선을 살펴보면 서울, 대전, 부산이 서로 관계가 있다는 것은 알 수 있지만, 각 도시가 얼마나 떨어져 있는지는 알 수 없다.
- 정점: 서울, 대전, 부산
- 간선: 서울—140km—대전, 대전—200km—부산, 부산—325km—서울
가중치 그래프 : 간선에 연결정도(거리 등)를 표현한 그래프
네비게이션은 간선에 거리를 표기한 가중치 그래프가 확장되어, 수백만개의 정점(주소)과 간선이 추가 되어야 비로소 내비게이션에서 쓰는 자료구조와 유사해진다.
그래프에서 사용하는 용어
- 무(방)향그래프(undirected graph): 모든 간선이 양방향으로 연결된 그래프
.png)
- 단방향(directed) 그래프 : 두 정점을 연결하는 간선에 방향이 존재하는 그래프, 간선의 방향으로만 이동할 수 있다.
.png)
정점 a와 b가 있고 이 둘을 이어주는 간선 c가 있다. 무방향 그래프에서는 a->b라면 b->a이며, a->b가 불가능하다면 b->a 역시 불가능하다. 반면 단방향 그래프에서는 정점 a에서 정점 b로 가는 간선 c가 있다면 이는 a->b를 의미할 뿐, b->a를 의미하는 것은 아니다.
- 진입차수(in-degree): 외부 노드에서 한 정점으로 들어오는 간선의 수
- 진출차수(out-degree): 한 정점에서 외부로 향하는 간선의 수
- 인접(adjacency): 간선에 의해 연결된 정점
- 자기 루프(self loop): 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우 자기 루프를 가졌다 라고 표현한다. 다른 정점을 거치지 않는다는 것이 특징.
- 사이클(cycle): 시작 정점과 종료 정점이 동일한 경우. 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있다면 사이클이 있다고 표현한다.
그래프 구현 방법
1. 인접행렬(Adjacency Materix)
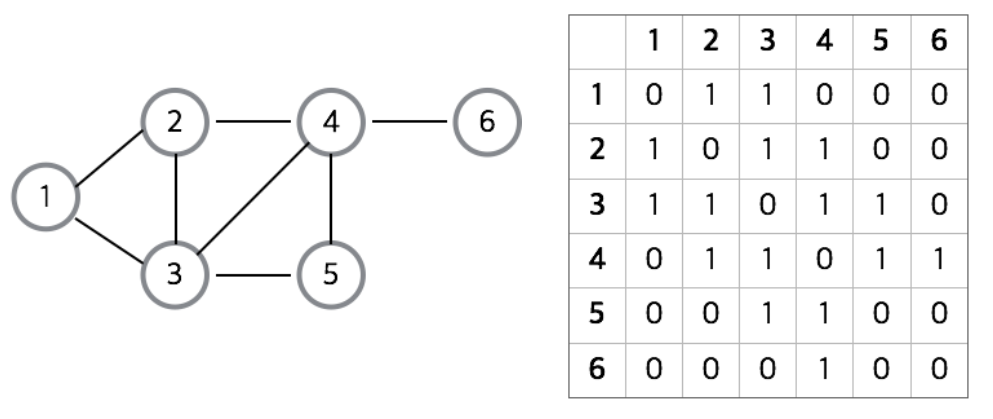
서로 다른 정점들이 인접한 상태인지를 표시한 행렬으로 2차원 배열의 형태로 나타낸다. 만약 A라는 정점과 B라는 정점이 이어져 있다면 1(true), 이어져 있지 않다면 0(false)으로 표시한다.
2. 인접리스트(Adjacency List)
.png)
각 정점이 어떤 정점과 인접한지를 리스트의 형태로 표현한다.
2. Tree
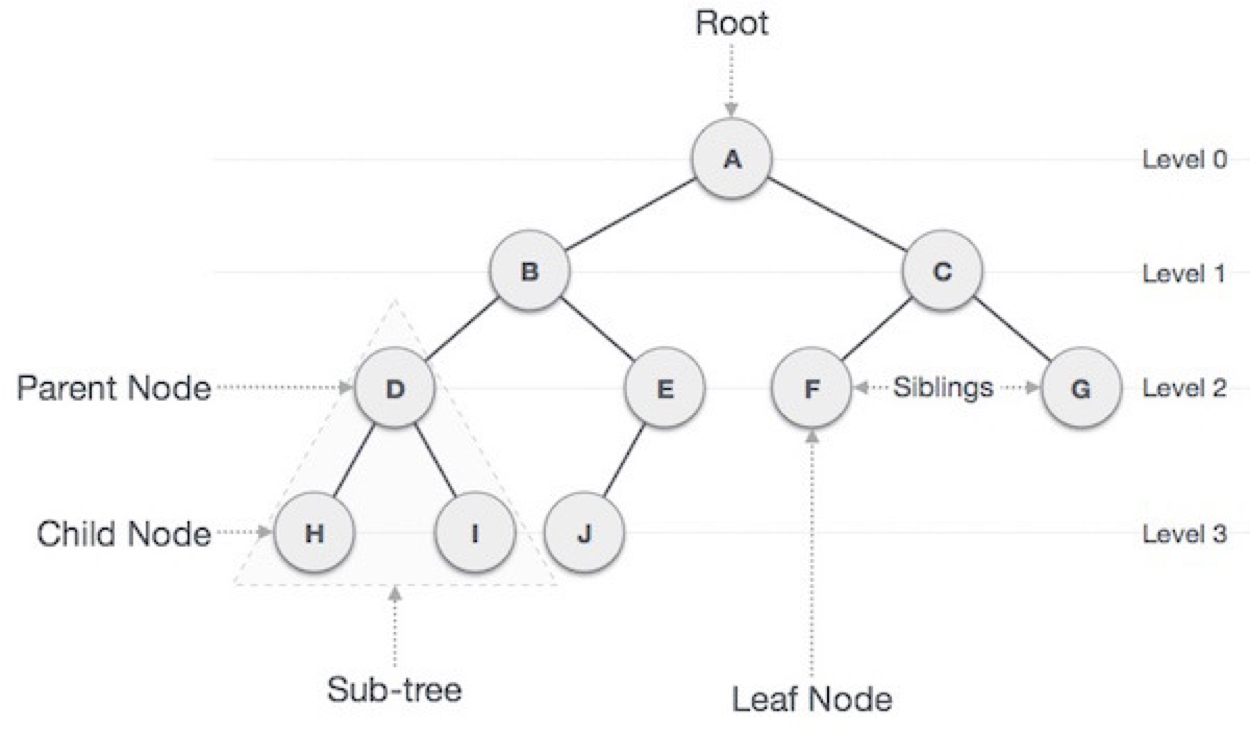
그래프의 여러 구조 중 무방향 그래프의 한 구조로, 하나의 뿌리로부터 가지가 사방으로 뻗은 형태가 나무와 닮아 있다고 해서 트리 구조라고 부른다.
1) 트리는 하나의 루트 노드를 갖는다.
2) 루트 노드는 0개 이상의 자식 노드를 갖고 있다.
그 자식 노드 또한 0개 이상의 자식 노드를 갖고 있고, 이는 반복적으로 정의된다.
3) 노드(node)들과 노드들을 연결하는 간선(edge)들로 구성되어 있다.
트리에서 사용하는 용어
- 루트 노드(root node): 트리 구조의 시작점이 되는 노드. 부모가 없는 노드이며 트리는 하나의 루트 노드만을 가진다.
- 단말 노드(leaf node): 트리 구조의 끝지점이고, 자식 노드가 없는 노드
- 내부(internal) 노드: Leaf 노드가 아닌 노드
- 형제(sibling): 같은 부모를 가지는 노드
- 노드의 크기(size): 자신을 포함한 모든 자손 노드의 개수
- 노드의 깊이(depth): 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- 노드의 레벨(level): 트리의 특정 깊이를 가지는 노드의 집합
- 노드의 차수(degree): 하위 트리 개수 / 간선 수 (degree) = 각 노드가 지닌 가지의 수
- 트리의 차수(degree of tree): 트리의 최대 차수
- 트리의 높이(height): 루트 노드에서 가장 깊숙히 있는 노드의 깊이