(python)백준-도시분할계획

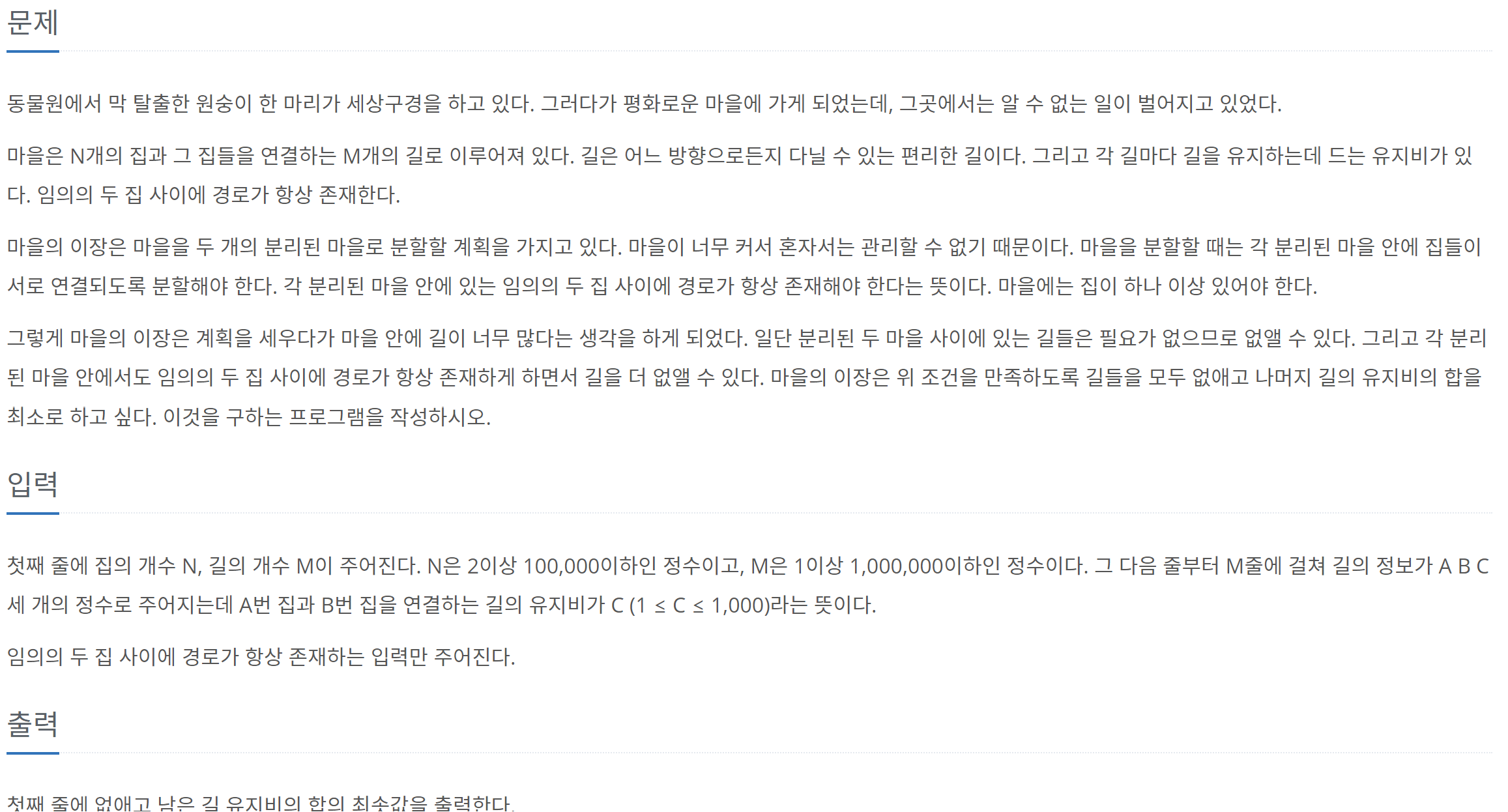
문제

최소신장트리를 이용해 푸는 문제이다.

핵심 아이디어는 최소신장트리를 2개 만들어야 하는 것인데
크루스칼 알고리즘으로 최소신장트리를 찾은 뒤 가장 비용이 큰 간선을 제거하면 된다.

import sys
n,m=map(int,sys.stdin.readline().split())

graph=[]

for i in range(m):
    a,b,c=map(int,sys.stdin.readline().split())
    graph.append((c,a,b))
graph.sort()

def find_parent(parent,x):
    if parent[x]!=x:
        parent[x]=find_parent(parent,parent[x])
    return parent[x]
def union_parent(parent,a,b):
    a=find_parent(parent,a)
    b=find_parent(parent,b)
    if a<b:
        parent[b]=a
    else:
        parent[a]=b

parent=[0]*(n+1)
#parent테이블 자기자신으로 초기화 
for i in range(1,n+1):
    parent[i]=i
#최종비용 변수
result=0
#마지막에 뺄 가장 비용이 큰 간선
last=0
for g in graph:
    cost,a,b=g
    if find_parent(parent,a)!=find_parent(parent,b):
        union_parent(parent,a,b)
        result+=cost
        last=cost
print(result-last)