[CS231N] Lecture 7 Training Neural Networks II

1. Fancier Optimization
Optimization(최적화) : 손실 함수(loss function)의 최솟값을 찾아나가는 일련의 과정으로, 역전파(backpropagation) 과정 중 가중치를 업데이트하면서 진행된다.
매 step마다 순방향 전파(forward pass)의 끝단에서 계산되는 손실 함수값은 지금까지 업데이트된 가중치들이 얼마나 잘 설정되어 있는지를 나타내는 지표와도 같다.
weight의 업데이트 = 에러 낮추는 방향(decent) x 한 발자국 크기(learning rate) x 현 지점의 기울기(gradient)
- learning rate(학습률) : 한 step마다 이동하는 보폭
- gradient(기울기) : 앞으로 이동할 방향
지금까지는 간단한 최적화 알고리즘인 확률적경사하강법(SGD)를 사용했으나 이 방법에는 단점이 있다.
SGD의 단점
1. Bad(High) condition number 발생
Condition number : 그 지점에서 행렬의 가장 큰 특이값과 가장 작은 특이값 사이의 비율로, 이 비율이 좋지 않으면 SGD가 잘 수행되지 않는다
SGD는 미니 배치 안에서 Loss를 계산하는데 Loss는 수직 방향의 가중치 변화에 훨씬 더 민감하게 반응하고 수평일 경우, 아주 미세하게 줄어든다. 그림과 같이 Loss가 2차원 상에 그려진다면, 빨간 점이 원점까지 가기 위해서는 수평이 아니라 수직적 이동을 해야 한다. 따라서 지그재그로 이동하기 때문에 아주 지저분하고 불안정하게 학습된다는 문제가 발생한다.
그림과 같이 Loss가 2차원 상에 그려진다면, 빨간 점이 원점까지 가기 위해서는 수평이 아니라 수직적 이동을 해야 한다. 따라서 지그재그로 이동하기 때문에 아주 지저분하고 불안정하게 학습된다는 문제가 발생한다.
2. local minima(극솟값)와 saddle point(안장점)
 기울기가 0(local minima)이거나 완벽히 0이 아니더라도 그 주변 경사가 굉장히 완만하여 매우 느리게 경사 하강하는 경우(saddle point), 최솟값이 아닌데도 기울기가 0이라 경사하강법이 멈춰버리는 문제가 발생한다.
기울기가 0(local minima)이거나 완벽히 0이 아니더라도 그 주변 경사가 굉장히 완만하여 매우 느리게 경사 하강하는 경우(saddle point), 최솟값이 아닌데도 기울기가 0이라 경사하강법이 멈춰버리는 문제가 발생한다.
local minima는 주로 2차원 그래프에서 흔히 나타나는 문제이고 saddle point는 고차원 그래프에서 흔히 발생하는 문제이다.
3. "확률적" 경사하강법
 SGD는 작은 미니 배치를 이용하여 손실을 추정하고 기울기를 추정하는 방식으로, 모든 단계에서 기울기에 대한 진정한 정보를 얻지 못한다.
SGD는 작은 미니 배치를 이용하여 손실을 추정하고 기울기를 추정하는 방식으로, 모든 단계에서 기울기에 대한 진정한 정보를 얻지 못한다.
→ 현재 지점에서 경사값에 대한 노이즈 추정치를 얻고 있다.
보완책
방향을 중심으로 하는 optimizer와 보폭을 중심으로 하는 optimizer로 분류할 수 있다.
- 방향 중심 : SGD + Momentum, NAG
- 보폭 중심 : AdaGrad, RMSProp
- 혼합 : Adam
1. SGD + Momentum
velocity term() : 속도를 조절하는 역할로 관성(Momentum) 효과를 낸다.
→ 로 이동할 때,
1) 속도 업데이트
지점에서의 속도를 전 단계인 지점에서의 속도를 기반으로 예측한다.
은 직전에서의 속도 와 기울기 를 고려하여 업데이트하고 이 때 기울기가 너무 빠르게 변하는 것을 방지하기 위해 마찰 계수 를 적용한다.
마찰 계수 : 주로 0.9나 0.99 사용
2) 가중치 업데이트
손실 함수에서 지점은 직전 지점 에서의 학습률 와 (= 지점에서의 예측 속도)를 고려해 업데이트된다.
매 step마다 gradient가 동일한 부호를 가지면 의 절댓값은 계속 증가할 수 밖에 없다. 이에 따라 의 변화 폭이 커지는데 즉, 같은 방향으로 이동할수록 더 큰 보폭으로 이동하여 가속화한다.
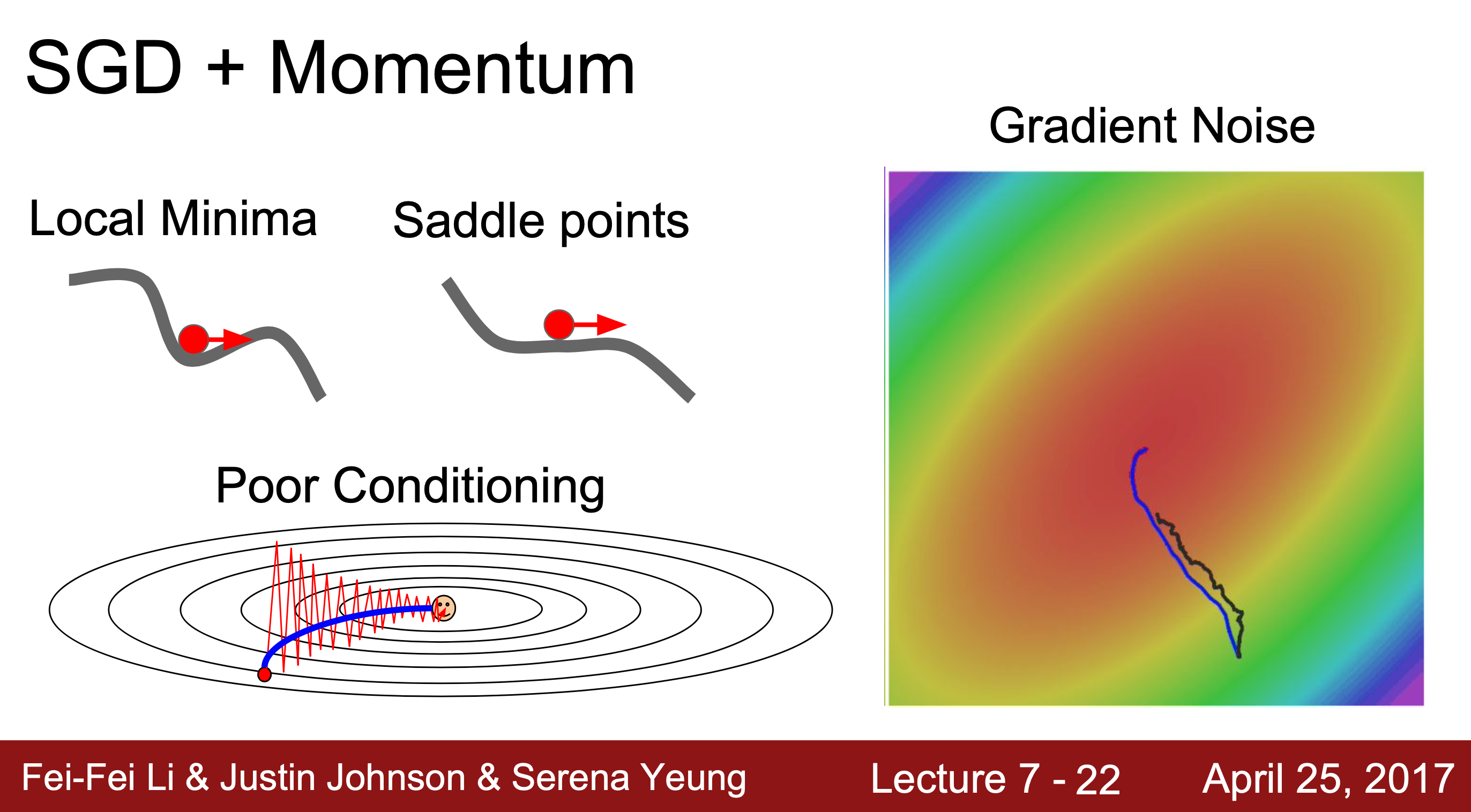 따라서, gradient가 0에 수렴하는 값을 가지더라도 이전 step들에서 축적되어온 가 더해지며 멈추지 않고 옆으로 탈출한다.
따라서, gradient가 0에 수렴하는 값을 가지더라도 이전 step들에서 축적되어온 가 더해지며 멈추지 않고 옆으로 탈출한다.
→ local minima나 saddle point에서의 SGD의 문제점을 해결할 수 있다.
또, 지그재그로 움직이는 상황이라면 momentum이 이 변동을 서로 상쇄시켜줌으로써 Loss에 민감한 수직 방향 변동은 줄여주고 수평 방향 변동은 점차 가속화한다.
→ High Condition Number 문제가 해결된다,
2. Nesterov Momentum (NAG)
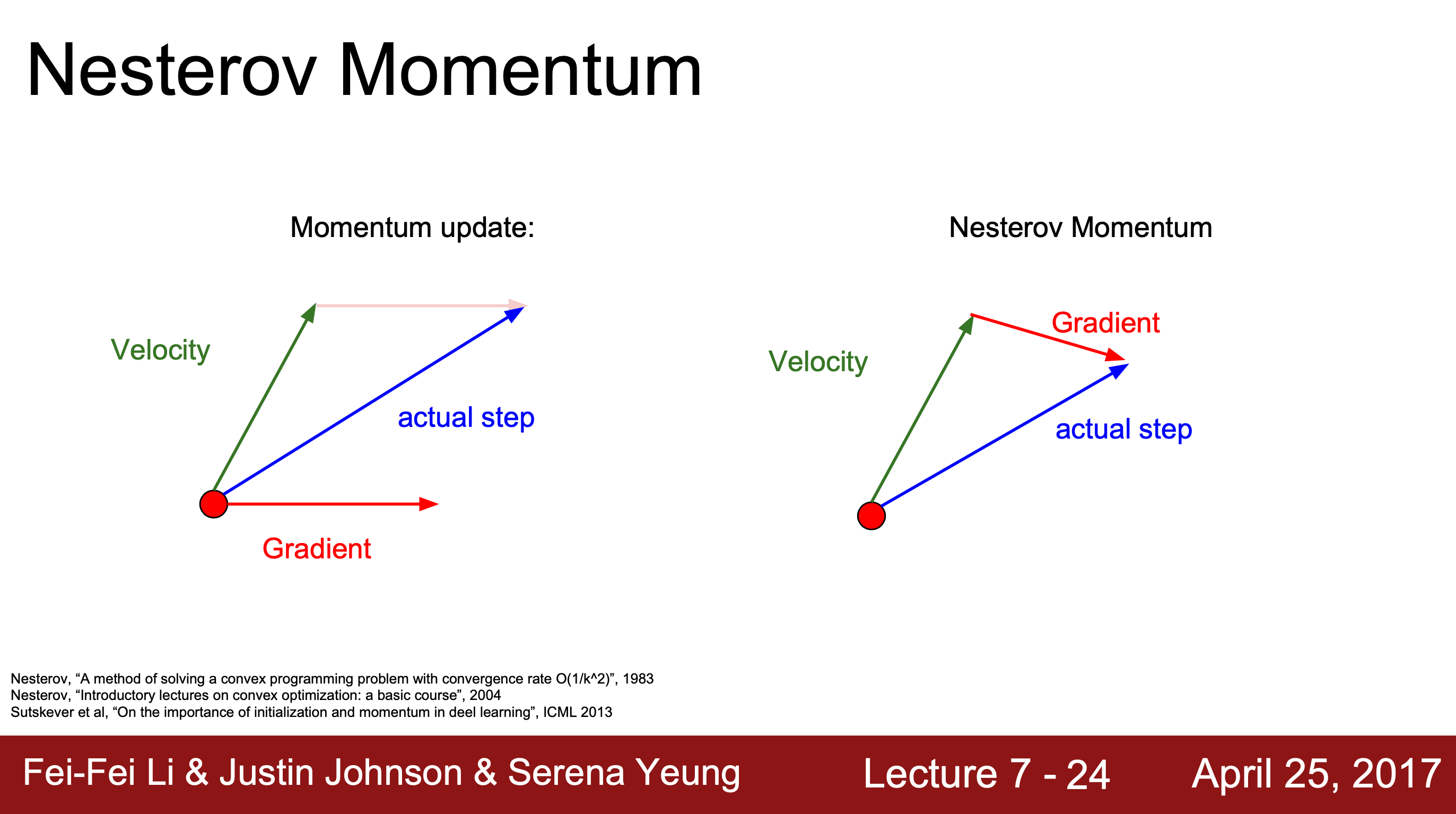
 이전 step의 속도 방향을 따라 먼저 이동하여 그 자리에서 gradient를 계산한 후, 다시 본래 자리로 돌아와 actual step으로 이동한다.
이전 step의 속도 방향을 따라 먼저 이동하여 그 자리에서 gradient를 계산한 후, 다시 본래 자리로 돌아와 actual step으로 이동한다.
→ gradient를 계산하는 지점과 실제 이동하는 지점이 다르다.
새롭게 변화된 식에서 error-correcting term이 발생하는데 이는 이전 속도와 현재 속도의 차이를 반영하여 급격한 슈팅을 방지하여 더 빠른 학습을 가능하게 한다.
3. AdaGrad
 기울기 제곱에 반비례하도록 학습률을 조정한다. 기울기가 가파를수록 조금씩 이동하고, 완만할수록 조금 더 이동함으로써 변동을 줄이는 효과가 있다.
기울기 제곱에 반비례하도록 학습률을 조정한다. 기울기가 가파를수록 조금씩 이동하고, 완만할수록 조금 더 이동함으로써 변동을 줄이는 효과가 있다.
step이 진행될수록 학습률이 작아지는데, 가중치마다 다른 학습률을 적용한다는 점에서 더 효과적인 정교화가 가능해진다.
또, 수평축과 수직축의 업데이트 속도를 적절히 맞춰준다.
다만 학습이 진행될수록 는 축적되고, 의 값이 커질수록 이와 반비례하여 이동하는 보폭은 줄어들게 된다.
→ 기울기가 0인 부근에서 학습이 급격하게 느려져 local minima나 saddle point에서의 SGD의 문제점이 다시 발생할 수도 있다.
이를 보완하고자 RMSProp가 등장하였다.
4. RMSProp
 AdaGrad와 식이 비슷하지만 보폭은 줄이면서, 이전 기울기 변화의 맥락을 살핀다는 차이가 있다. 누적된 기울기 제곱에 decay_rate를 곱하고 현재의 dx항에는 (1- decay_rate)를 곱해 기울기 제곱이 누적되는 속도를 줄여준다.
AdaGrad와 식이 비슷하지만 보폭은 줄이면서, 이전 기울기 변화의 맥락을 살핀다는 차이가 있다. 누적된 기울기 제곱에 decay_rate를 곱하고 현재의 dx항에는 (1- decay_rate)를 곱해 기울기 제곱이 누적되는 속도를 줄여준다.
보통 decay_rate(= p)는 0.9로 설정되는데 이전 step의 기울기를 더 크게 반영하여 값이 단순 누적되는 것을 방지해준다.
5. Adam
+) Adam 관련 정리 블로그
 방향을 중심으로 하는 Momentum 계열과 보폭을 중심으로 하는 Ada 계열이 합쳐져 보폭 & 방향을 모두 적절하게 조절해준다.
방향을 중심으로 하는 Momentum 계열과 보폭을 중심으로 하는 Ada 계열이 합쳐져 보폭 & 방향을 모두 적절하게 조절해준다.
6. 그 외
Optimizer 외에도 학습률을 조정하는 방법들이 있다.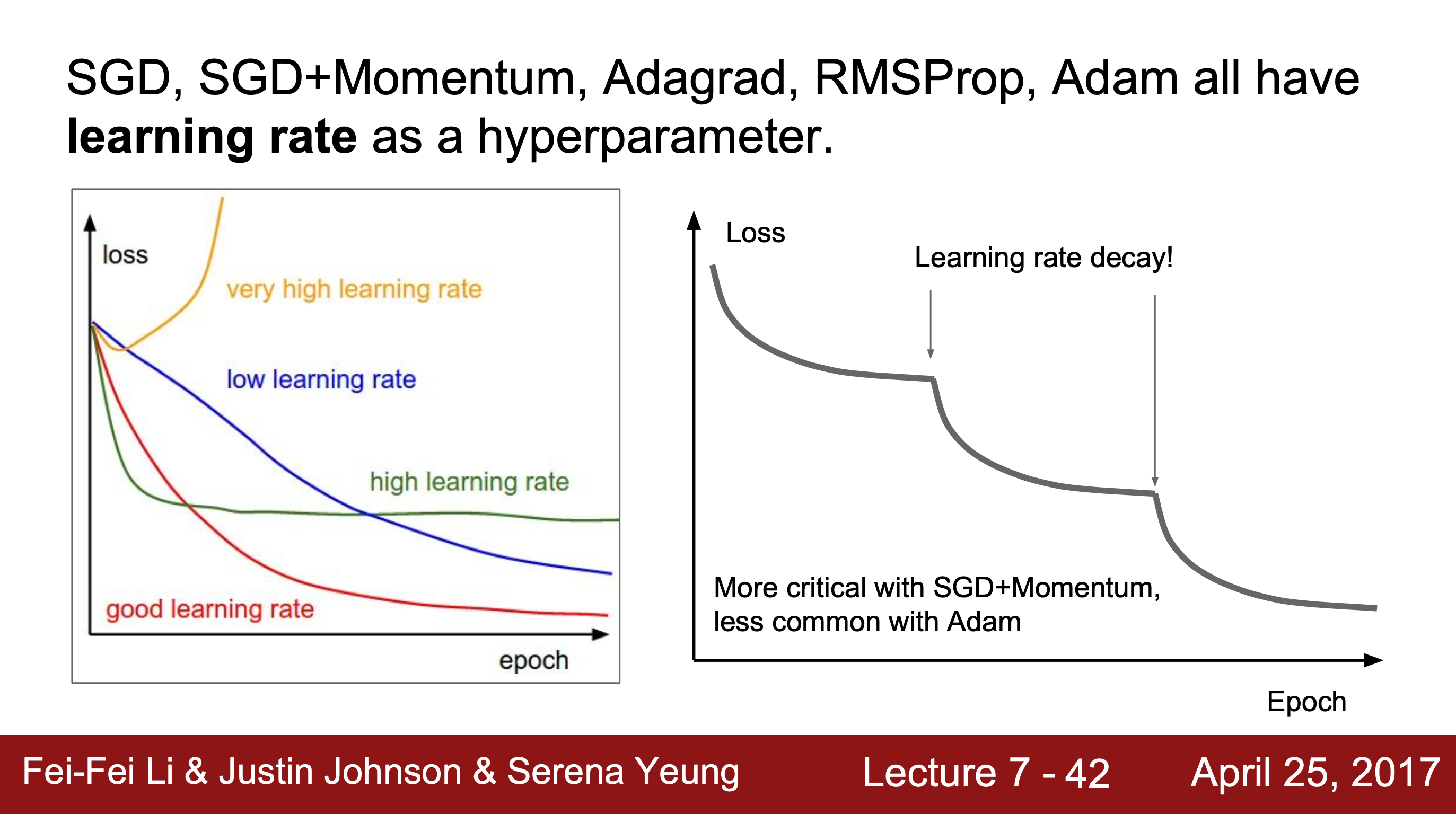 단, learning rate decay는 처음부터 쓰는 것이 아니라 학습과정을 모니터링한 후에 학습이 더딘 지점 등 필요하다고 생각되는 시점에 사용해야 한다.
단, learning rate decay는 처음부터 쓰는 것이 아니라 학습과정을 모니터링한 후에 학습이 더딘 지점 등 필요하다고 생각되는 시점에 사용해야 한다.
2. Regularization
Optimization이 training error를 줄이고자 노력했다면,
Regularization은 valid error와의 차이를 줄여 과적합을 방지하고자 한다.
Model Ensembles
앙상블은 Regularization 기법은 아니다. 하지만 최적의 test 결과를 만들어 내기 위한 방안으로,
- 여러 모델을 독립적으로 학습하여 test 결과를 평균 내기
- 하나의 모델에서 여러 번 스냅샷 찍어 학습률이 크게 변동할 때 완화해주기
와 같은 방식으로 수행할 수 있다.
→ 급격한 개선은 아니지만 지속적인 개선에는 도움이 되는 방법으로, 과적합이 약간 줄어들고 성능이 조금 향상된다.
Single-Model Regularization
1. L1, L2 Regularization

- L1 : 학습에 기여하지 못하는 가중치를 0으로 보내버린다.
- L2 : 학습에 기여하지 못하는 가중치를 0에 가까운 값으로 제한한다.
- : 규제(regularization) 강도
2. Dropout
 랜덤으로 뉴런의 값을 0으로 설정해버리는 방법으로,
랜덤으로 뉴런의 값을 0으로 설정해버리는 방법으로,
주로 Fully Connected Layer에서 사용되고 Convolution Layer에서는 보통 채널(전체 Map) 단위로 적용된다.
효과
1. 과적합 방지
학습을 시키다 보면 비슷한 정보를 가지는 노드들이 생기는데 이는 과적합의 원인이 되기도 한다.
→ 입력값의 일부를 0으로 두어 backpropagation(역전파) 시 파라미터가 업데이트 되지 않게 되고, 이는 모형의 불확실성을 증가시켜 과적합을 방지할 수 있다.
2. 앙상블 효과
학습을 할 때마다 임의로 dropout시키기 때문에 매번 다른 모델을 만드는 것과 같은 앙상블 효과가 나타나기도 한다.
학습 단계뿐만 아니라 Test 단계에서도 Dropout이 사용될 수 있다.
 학습 시에는 Zero Mask를 임의로 부여한다. test 단계에서는 임의성을 부여하면 안되기 때문에 확률값을 곱하여 기댓값을 구해 평균화하거나 그냥 사용하기도 한다.
학습 시에는 Zero Mask를 임의로 부여한다. test 단계에서는 임의성을 부여하면 안되기 때문에 확률값을 곱하여 기댓값을 구해 평균화하거나 그냥 사용하기도 한다.
cf> DropConnect : 뉴런이 아니라 가중치를 임의로 0으로 만드는 방식
3. Batch Normalization
 ; 배치 정규화
; 배치 정규화
train에서 미니 배치를 샘플링하며 임의성을 부여하고, test에서는 전체 단위로 정규화하여 평균화하는 효과를 낸다.
4. Data Augmentation
단순하게 학습 데이터의 양을 늘려 과적합을 해결하는 방법이다.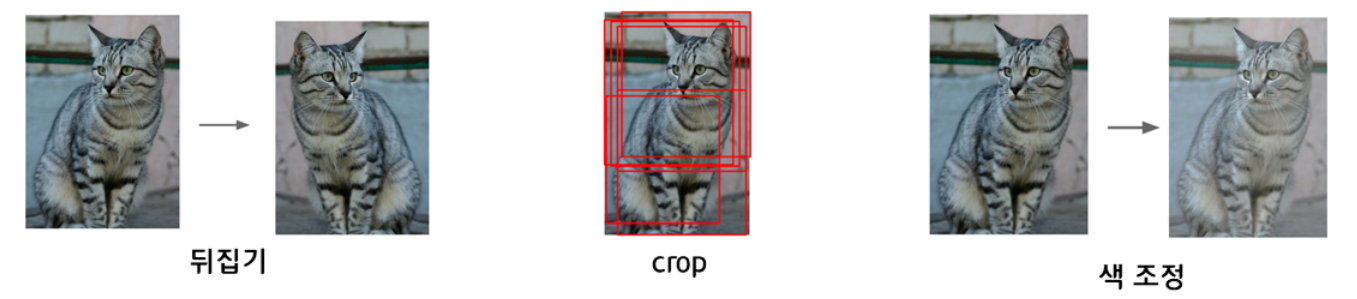 기존의 데이터를 가공해 새로운 버전을 만듦으로써 데이터의 양을 늘릴 수 있다.
기존의 데이터를 가공해 새로운 버전을 만듦으로써 데이터의 양을 늘릴 수 있다.
→ 데이터가 늘어나면서 학습 시 임의성이 부여되기 때문에 모델의 일반화에 용이해진다.
Regularization Summary
- Train 시, 모델에 임의성(Randomness) 부여
- Test 시, 이를 평균화하여 균일하게 학습 효과 적용
3. Transfer Learning
전이학습이란, 충분한 양의 데이터로 이미 학습된 모델을 활용하여 우리의 데이터셋을 학습시키는 방법이다.
우리가 가진 데이터가 모델을 학습시키기에 매우 부족한 양일 때, 전이학습이 효과적으로 사용될 수 있다.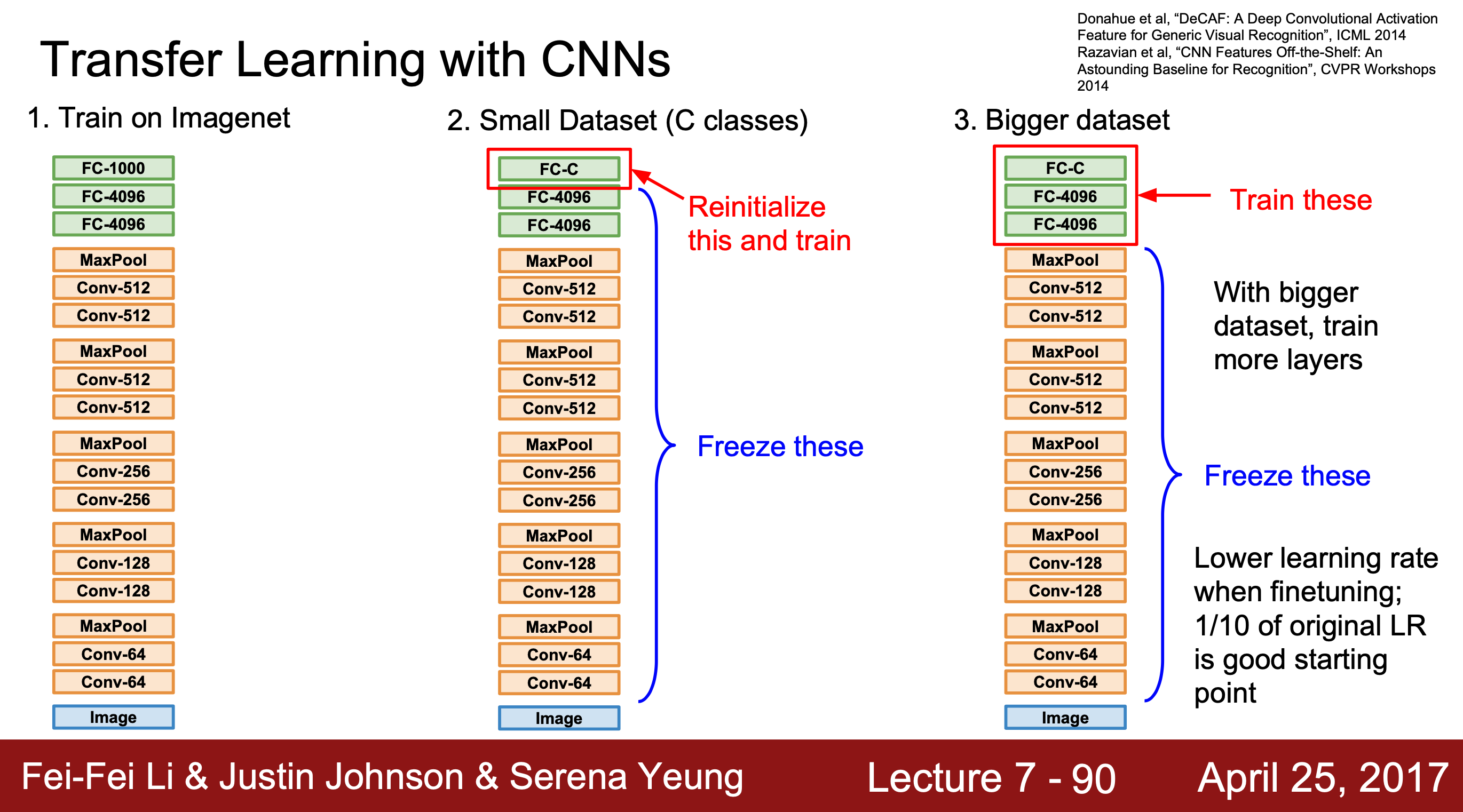
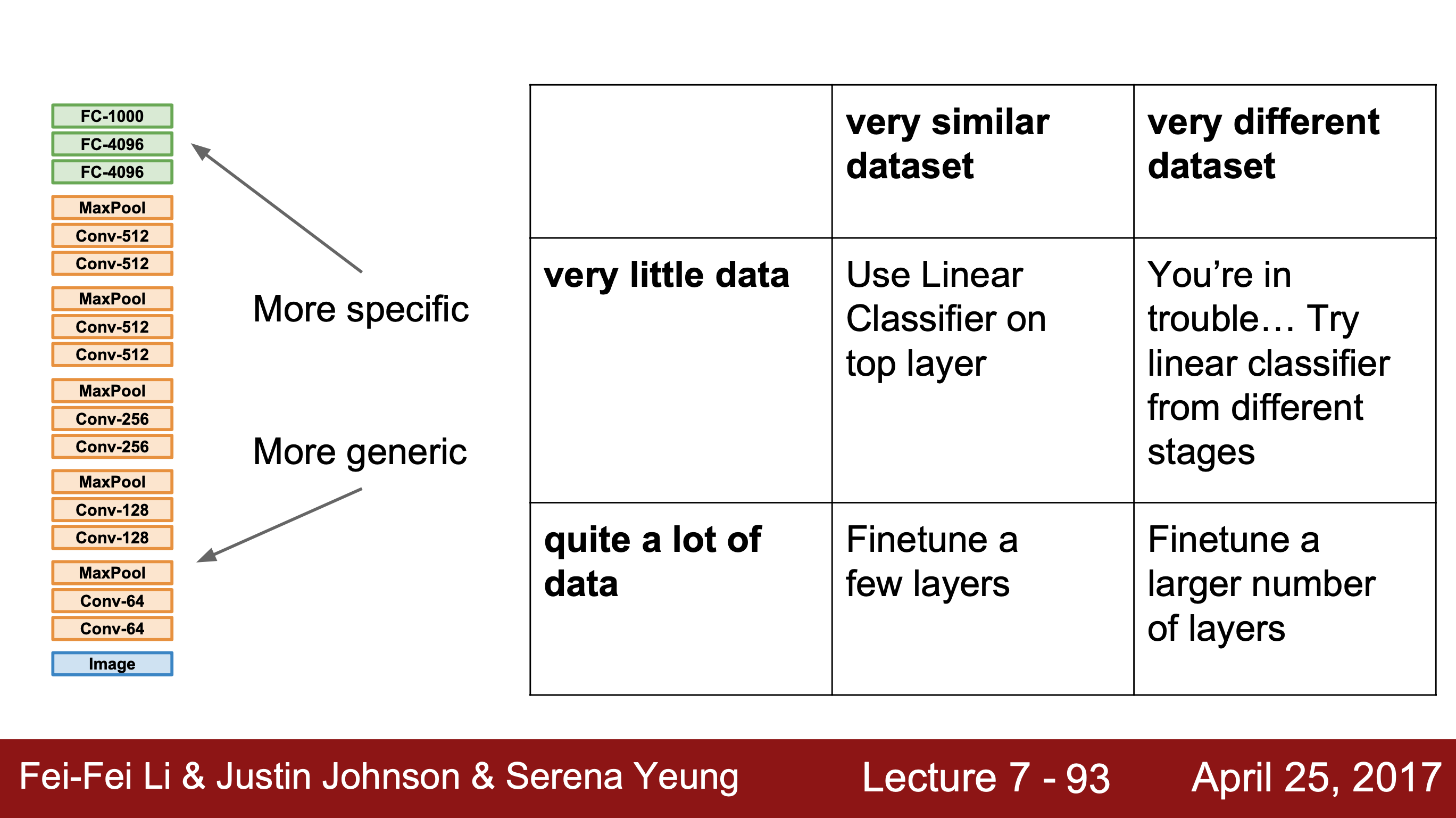
- 학습 데이터 셋의 양이 매우 적은 경우, 마지막 FC Layer을 제외하고 모든 층의 가중치를 고정시켜 학습시킨다.
- 데이터 셋의 양이 조금 더 큰 경우, 가중치를 학습시킬 층을 늘린다.
최적화 알고리즘, 특히 Adam은 식이 Ada계열과 Momentum계열이 섞인데다 적률도 나와 강의만 볼 때는 이해하기 어려웠는데 잘 정리된 블로그를 찾아 큰 도움이 되었다 👍🏻