[Lab-04-1] Multivariable Linear regression
- Simple Linear Regression : 하나의 정보로부터 하나의 결론을 짓는 모델
H(x) = Wx + b (x라는 vector와 W라는 matrix의 곱) - Multivariable Linear regression : 복수의 정보로부터 하나의 추측값을 계산하는 모델
1. H(x) = w1x1 + w2x2 + w3x3 + b
(입력변수가 3개일 경우, weight도 3개 -> w와 x 모두3x1 vector)
X의 길이가 길어진다면(=정보가 많아진다면) 위의 식도 점점 길어짐
Solution)
PyTorch에서 제공해준 matmul() 함수 사용 -> 간결하고 빠른 코드 탄생
matmul() = matrix multiplication
2. Cost function : (Simple Linear Regression와 동일하게) MSE(Mean Squared Error) 사용
MSE : 예측값과 실제값의 차이를 제곱한 평균3. 학습방법 : (Simple Linear Regression와 동일하게)
○1 optimizer 설정
○2 cost를 구할 때마다 optimizer의 gradient에 저장
○3 gradient descent 시행
Simple Linear Regression과의 차이점 : 데이터(모델)를 정의하는 부분 & W를 정의하는 부분
학습한 부분이 Simple Linear Regression와 동일하다 -> PyTorch의 확장성이 나타남
4.
4-1. nn.Module
cf> 모델이 커질수록 W와 b를 일일이 쓰기 힘들다.
Solution)
PyTorch에서 제공해준 nn.Module() 모듈 사용
ex)
<기존 코드(모델이 작을 때)>
#모델 초기화
W = torch.zeros((3 , 1), requires_grad = True)
b = torch.zeros((1, requires_grad = True)
#H(x) 계산
hypothesis = x_train.matmul(W) + b
<nn.Module() 사용(모델이 클 때)>
import torch.nn as nn
class MultivariateLinearRegressionModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(3, 1)
def forward(self, x):
return self.linear(x)
hypothesis = model(x_trian)
nn.Module 상속 -> 모델 생성
nn.Linear(3, 1) ; 입력 차원 = 3, 출력 차원 = 1
forward 함수 : hypothesis 계산을 어떻게 하는지 설정
4-2. F.mse_loss
<기존의 코드(모델이 작을 때>
#cost 계산
cost = torch.mean((hypothesis – y.train) ** 2)
<F.mse_loss 사용(모델이 클 때)>
import torch.nn.functional as F
#cost 계산
cost = F.mse_loss(prediction, y_train)
cost 계산 시 loss function 사용하는 이유
○1 쉽게 다른 loss와 교체 가능
○2 cost를 계산하면서 생기는 버그가 없어 디버깅할 때 편리함
[Lab-04-2] Loading Data
Review)
Simple Linear Regression : 하나의 정보로부터 하나의 결론을 짓는 모델
Multivariable Linear Regression : 복수의 정보로부터 하나의 추측값 계산
Data in the Real World
- 대부분의 데이터셋은 적어도 수십만 개의 데이터를 제공한다.
장점 : 모델이 많은 데이터를 학습하면서 더 견고하고 완성된 예측 가능
단점 : 연산 속도가 느려지거나 하드웨어적으로 불가능해짐(컴퓨터에 저장X) - 데이터셋에 있는 모든 데이터를 한 번에 학습시키는 것은 불가능하다.
1. Minibatch Gradient Descent
: 전체 데이터를 Minibatch라는 작은 양으로 균일하게 나누어 각 Minibatch마다 학습하는 방법
데이터셋의 일부분만 학습
<기존> 컴퓨터가 데이터셋의 모든 데이터의 cost를 다 계산한 후 gradient descent
각 Minibatch에 있는 데이터의 cost만 계산한 후 gradient descent
○+ 한 번의 업데이트마다 계산할 cost의 양은 줄어들고 그에 따른 업데이트 주기가 빨라짐
○- 전체 데이터를 쓰지 않게 되므로 모델이 가끔 잘못된 방향으로 학습할 수 있음
기존의 gradient descent처럼 cost가 매끄럽게 줄어들지 않고 좀 더 거칠게 줄어듦
2. PyTorch Dataset과 dataloader (PyTorch에서 제공하는 모듈)
-
PyTorch Dataset
○1 torch.utils.data.Dataset 상속
○2 새로운 클래스 만들기 => 우리가 원하는 dataset(CustomDataset) 지정
CustomDataset을 만들 때 필요한 magic method
○1 len() : dataset의 총 데이터 개수 반환
○2 getitem() : 어떤 인덱스를 입력받았을 때, 그에 상응하는 데이터 하나를 반환
○3 len(), getitem()을 거쳐 얻은 입출력 데이터를 torch.tensor 형태로 바꾸어서 반환 -
PyTorch DataLoader
○1 torch.utils.data.DataLoader 상속
○2 dataloader의 인스턴스를 만들 때 필요한 두 가지
○1 PyTorch Dataset으로 만든 CustomDataset
○2 각 Minibatch의 크기 : 통상적으로 2의 제곱수(16, 32, 64,128,…)로 설정
+)
○3 shuffle : 매번 데이터가 학습되는 순서를 바꾸는 옵션(
Shuffle = True ; 우리의 모델이 데이터셋의 순서를 외우지 못하게 방지할 수 있음
3. Full Code
nb_epochs = 20
for epoch in range(nb_epochs + 1):
for batch_idx, samples in enumerate(dataloader): x_train, y_train = samples
#H(x) 계산
prediction = model(x_train)
#cost 계산
cost = F.mse_loss(prediction, y_train)
#cost로 H(x) 개선 optimizer.zero_grad() cost.backward() optimizer.step()
print('Epoch {:4d}/{} Batch {}/{} Cost: {:.6f}'.format( epoch, nb_epochs, batch_idx+1, len(dataloader), cost.item()
))
- enumerate(dataloader) : minibatch의 인덱스와 데이터를 받음 -> 이 데이터를 x, y로 나누어서 gradient descent 시행
[Lab-05] Logistic Regression
Reminder
Logistic Regrssion = Binary Polification 문제
: d차원(d 사이즈)의 1d vector가 주어졌을 때, 0 또는 1 중 어떤 쪽에 가까운지 구하기

W : 모델 파라미터(weight 파라미터)
X : m d차원
W X 후 sigmoid 함수를 사용해 0과 1에 근사하도록 만듦
Sigmoid 함수 : -∞ = 0 / +∞ = 1에 가까운 값을 갖게 해주는 함수
σ(x)=1/(1+e^(-x))
H(x)가 0 또는 1이 되도록 만들어준다.
H(x) = 어떤 샘플이 1일 확률
= P(x = 1; w)
= 1- P(x = 0)
Ex)
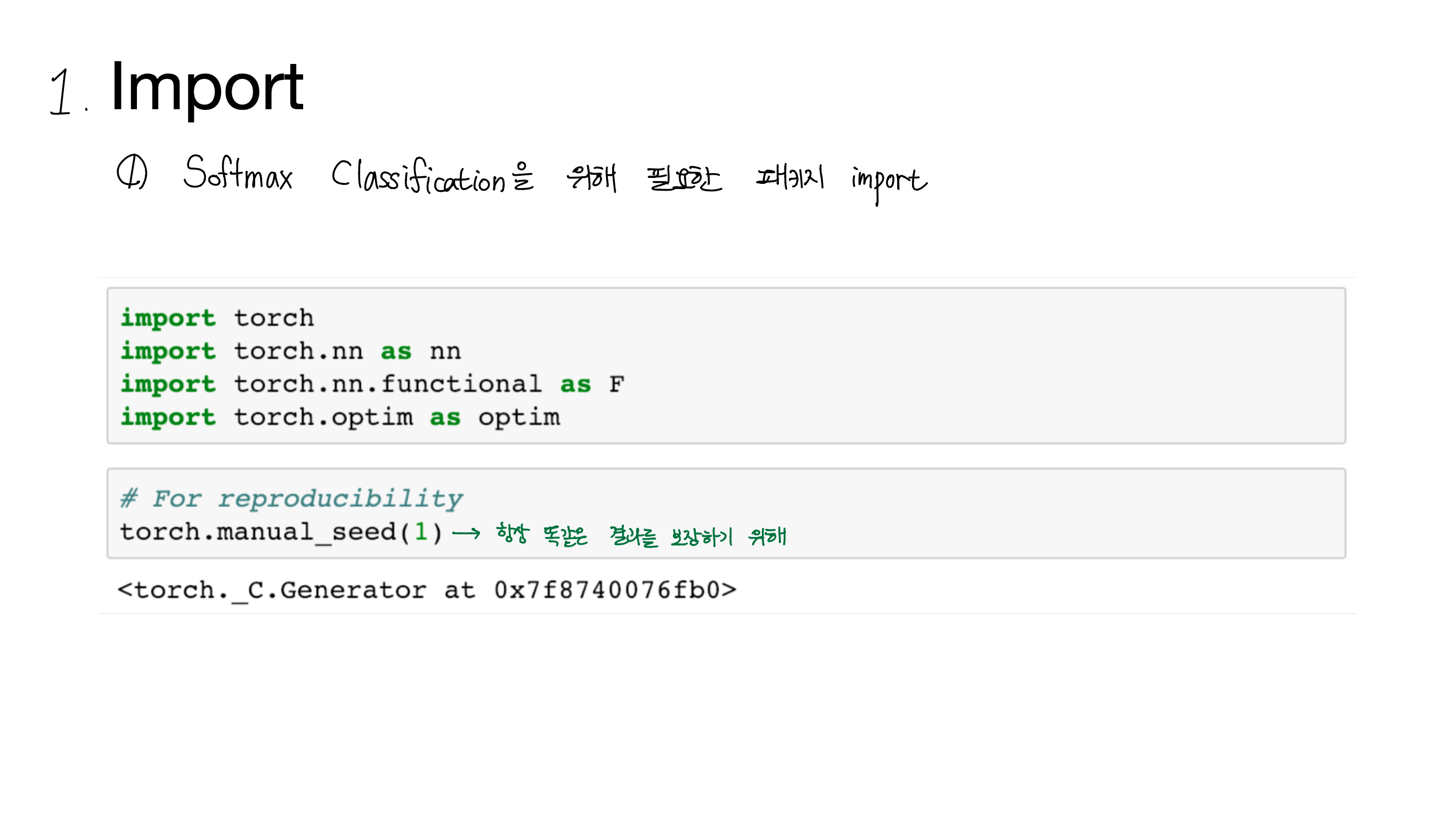
Imports
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
torch.manunal_seed(1)
Training Data
x_data = [[1, 2], [2, 3], [3, 1], [4, 3], [5, 3], [6, 2]]
y_data = [[0, [0], [0], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)
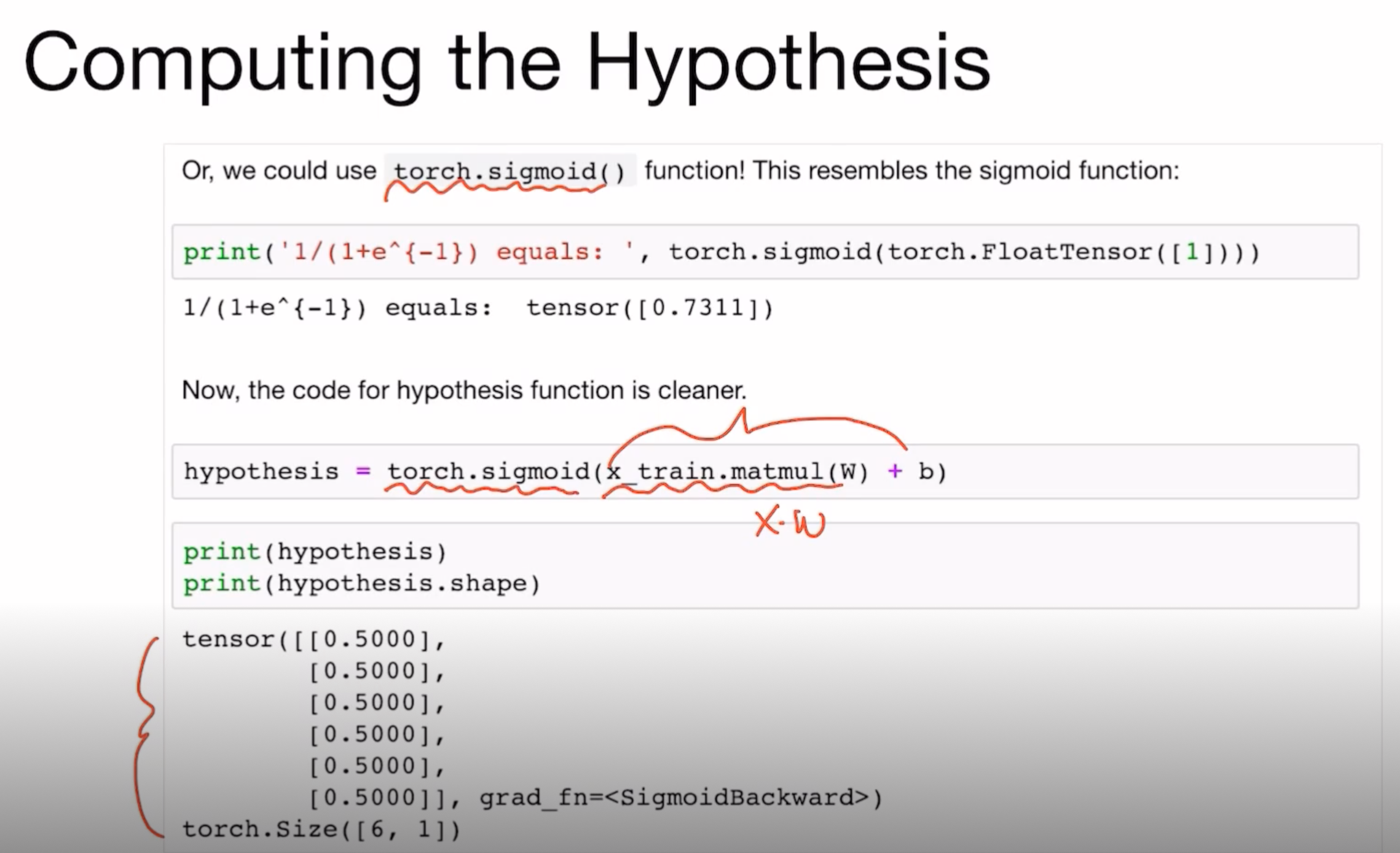
Computing the Hypothesis

Hypothesis 계산 부분을 sigmoid함수를 사용하게 되어도 같은 H(x)값을 나오는 것을 볼 수 있다.
Computing the Cost Function
하나의 원소로만 살펴보면,
- (y_train[0] torch.log(hypothesis[0] + ( 1 – y_train[0]) torch.log(1 – hypothesis[0]))
#tensor([0.6931], grad_fn=)
이때 torch.log(hypothesis[0]) = log P(x = 1; w),
torch.log( 1 - hypothesis[0]) = log P(x = 0; w) = 1 - log P(x = 1; w)이고,
y_train[0] = 1이면 1 – y_train[0] = 0, y_train[0] = 0이면 1 – y_train[0] = 1이다.
위 네 값 모두 스칼라이다.
전체 원소를 사용한 코드는 아래와 같다.
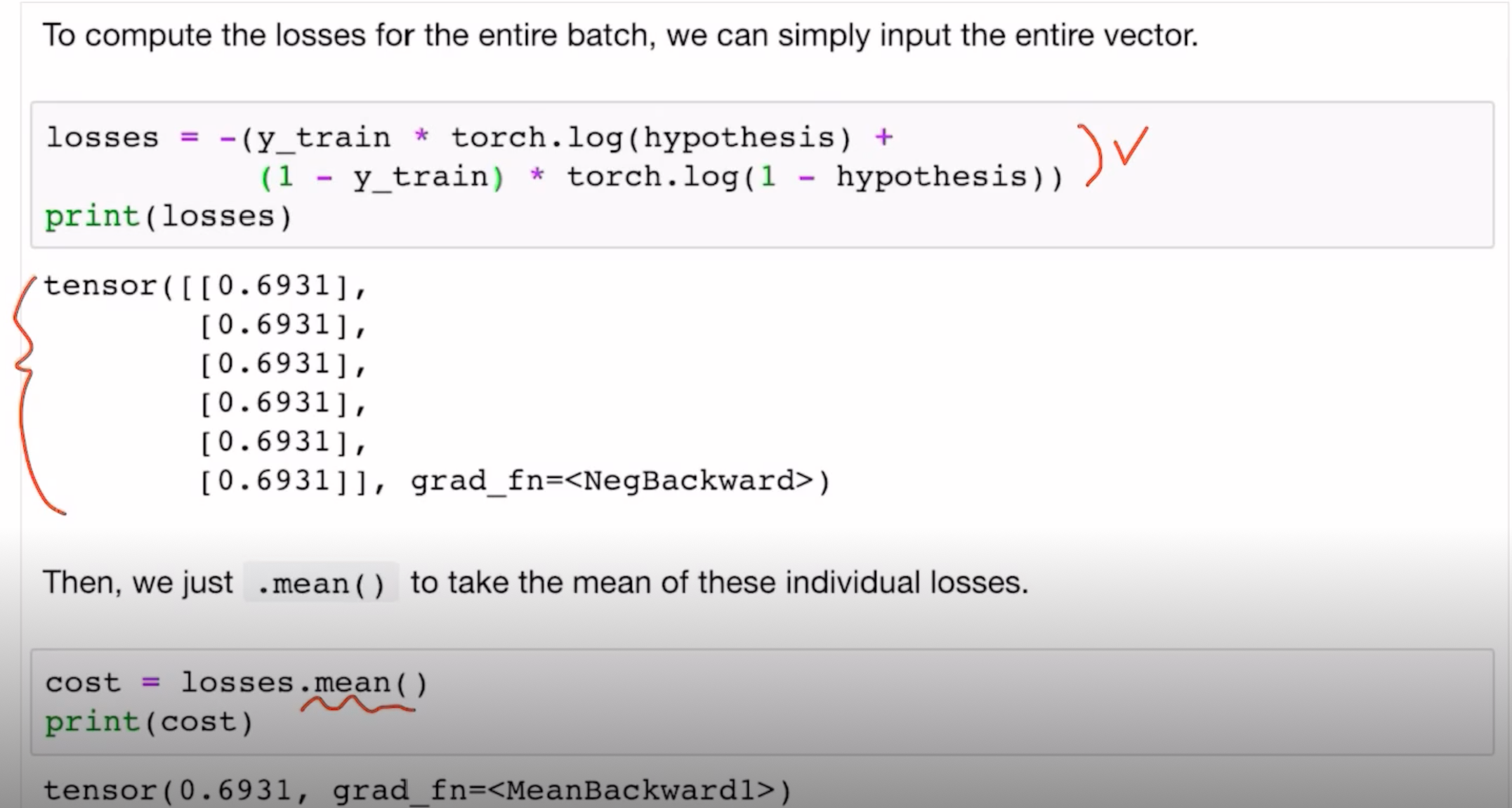
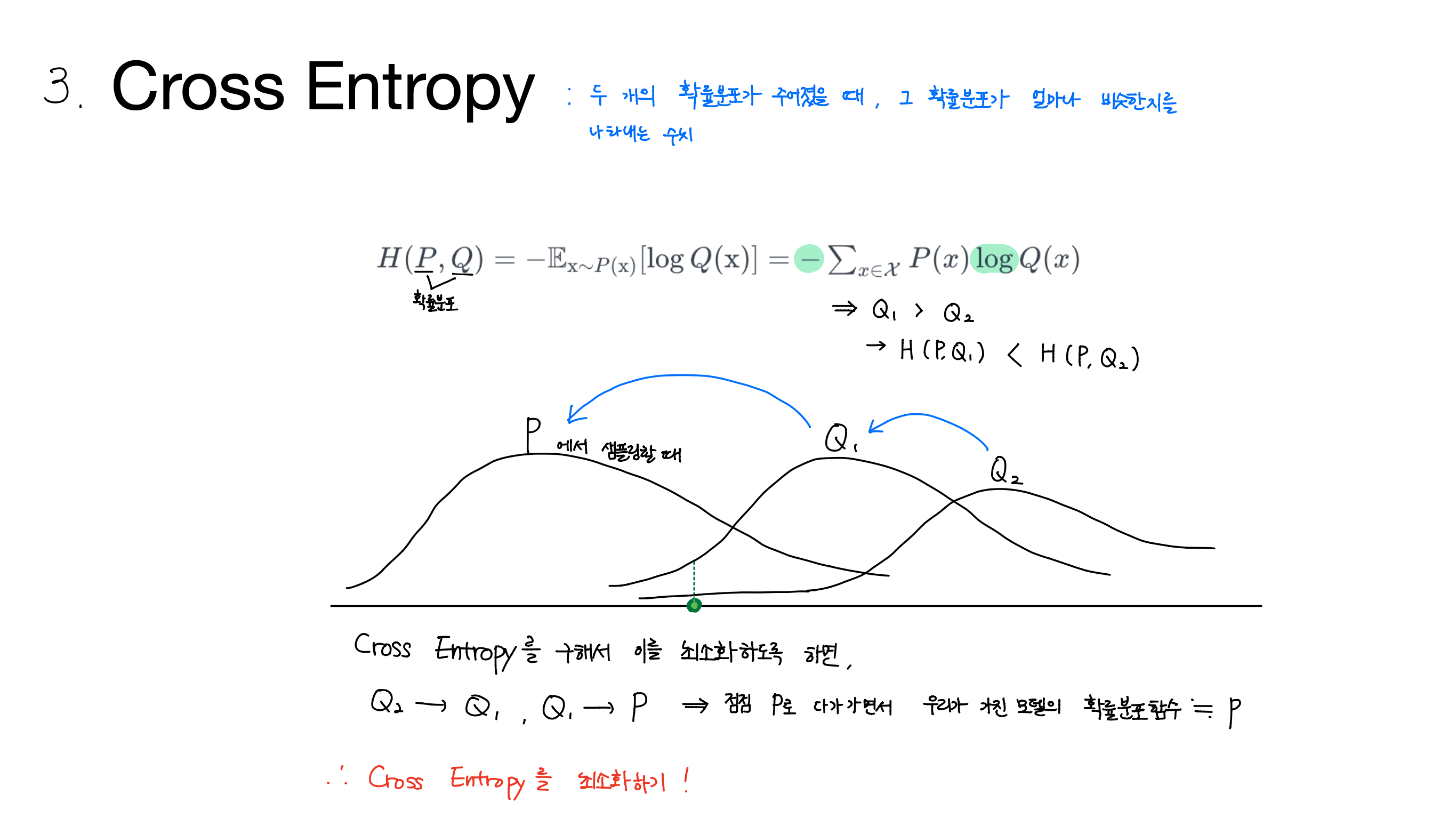
cf.> cost값 한 번에 구하기 -> binary_cross_entropy() 함수 사용하기
: binary class인 경우에 대한 cross entropy 구하는 것
F.binary_cross_entropy(hypothesis, y_train)
#tensor(0.6931, grad_fn=)
Whole Training Procedure
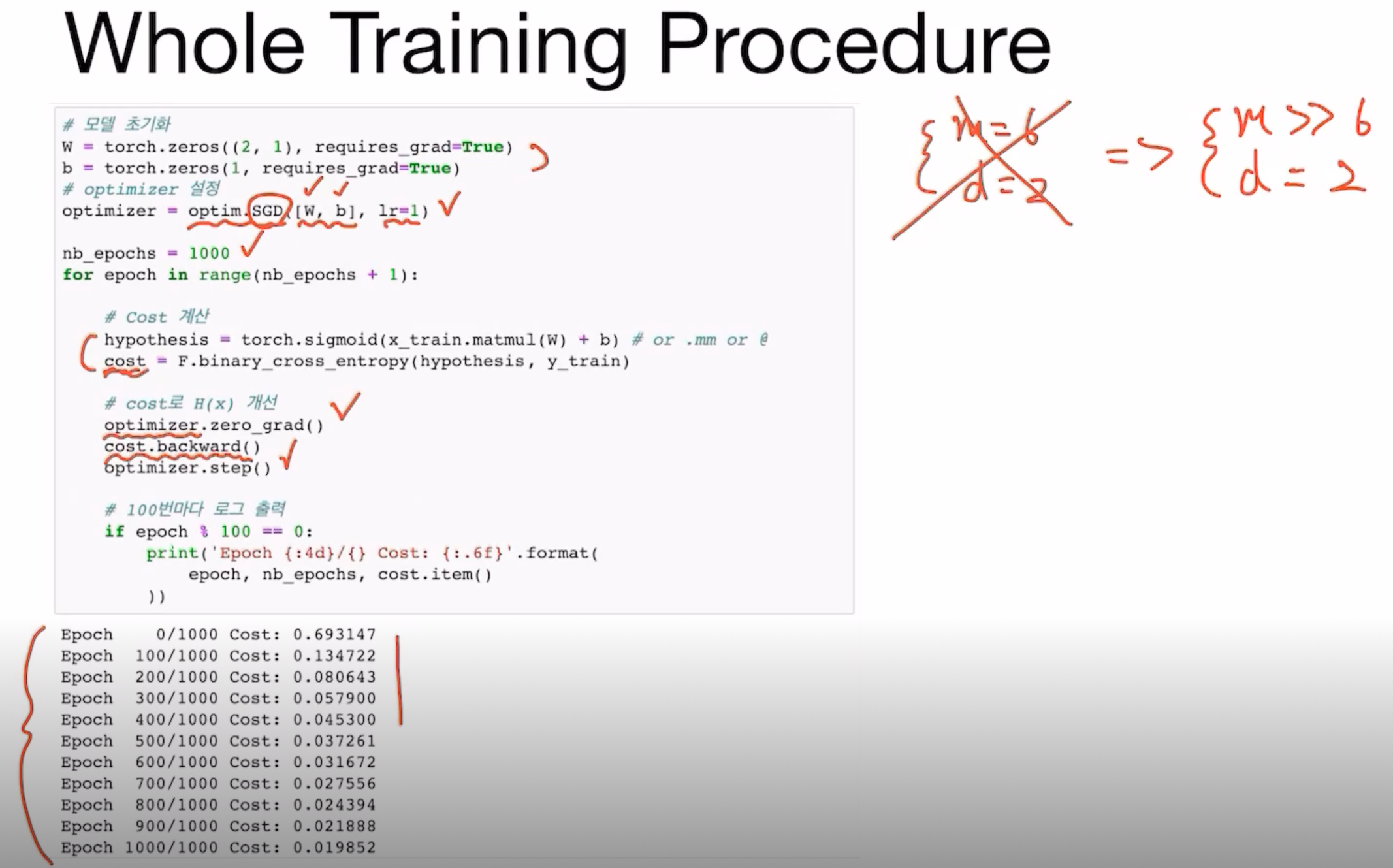
Optimizer에서 SGD를 이용해 learning rate가 1인 상태로 W와 b를 학습시킨다.
optimizer가 W와 b를 업데이트한다.
Optimizer가 optimization을 수행하기 전에 zero_grad() 함수를 호출해서 기존에 구해둔 gradient가 있으면 다시 0으로 초기화해준다.
( ∵초기화를 하지 않으면 gradient를 구할 때마다 기존에 구해둔 gradient에 더하게 됨)
cost.backward() ; cost back propagation 수행 -> 이제까지 연산에 사용되었던 W와 b에 gradient가 구해지게 된다.
Optimizer.step() ; cost값을 gradient를 사용하여 최소화하는 방향으로 W와 b를 업데이트해준다.
Cost가 점점 줄어드는 것을 확인할 수 있다.Evaluation
모델을 학습시킨 후, 성능테스트를 수행한다.
Ex)
hypothesis = torch.sigmoid(x_test.matmul(W) + b)
print(hypothesis[:5]) #결과값 5개만 출력
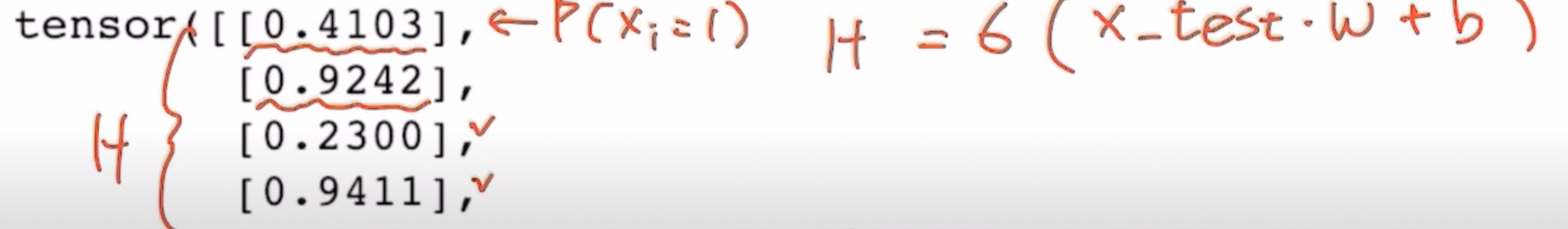
prediction = hypothesis >= torch.FloatTensor([0.5])
#hypothesis가 0.5이상이면 1, 미만이면 0으로 prediction에 저장한다.
#prediction과 y_train을 비교해 서로 일치하는지 확인해준다.
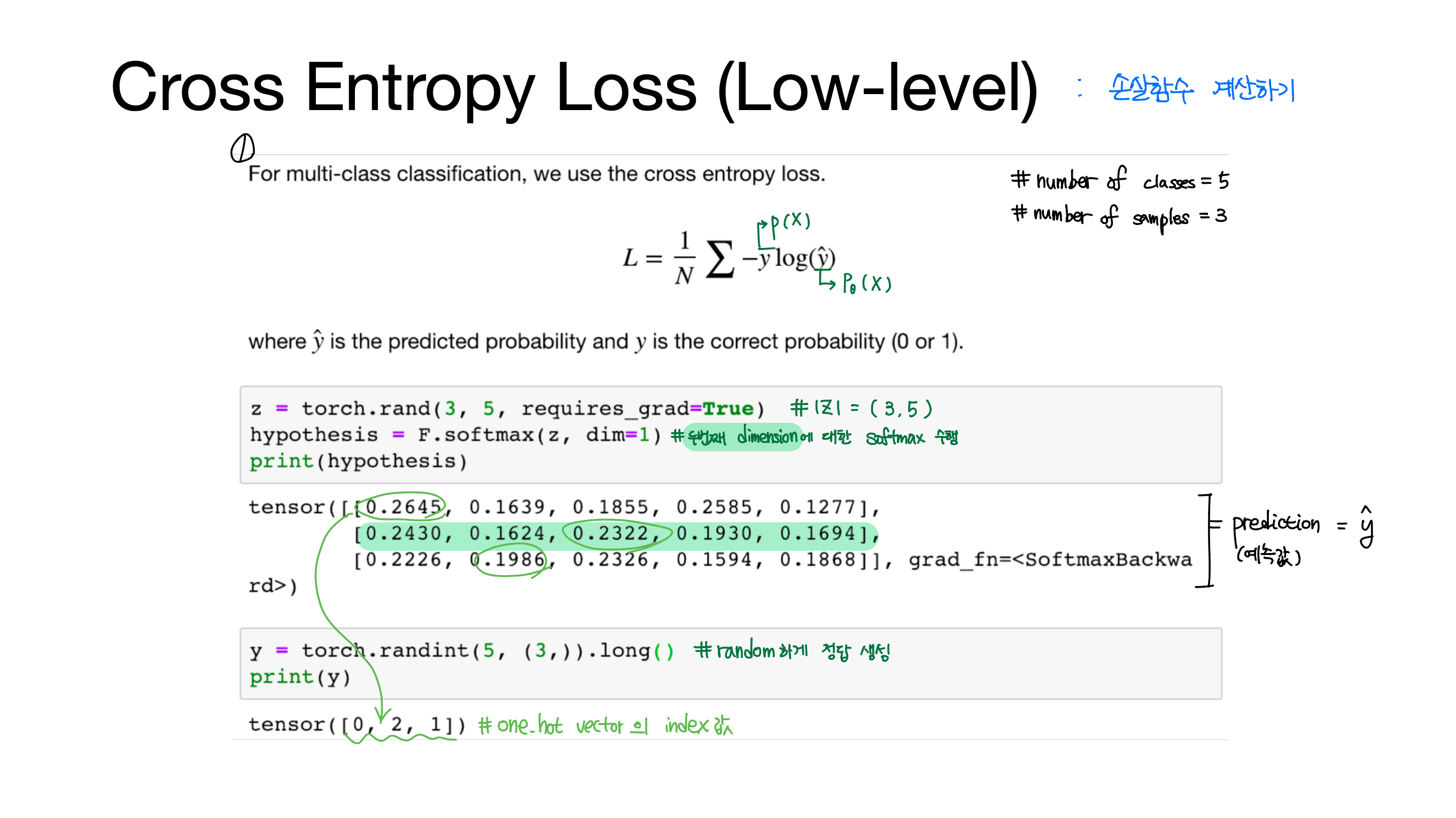
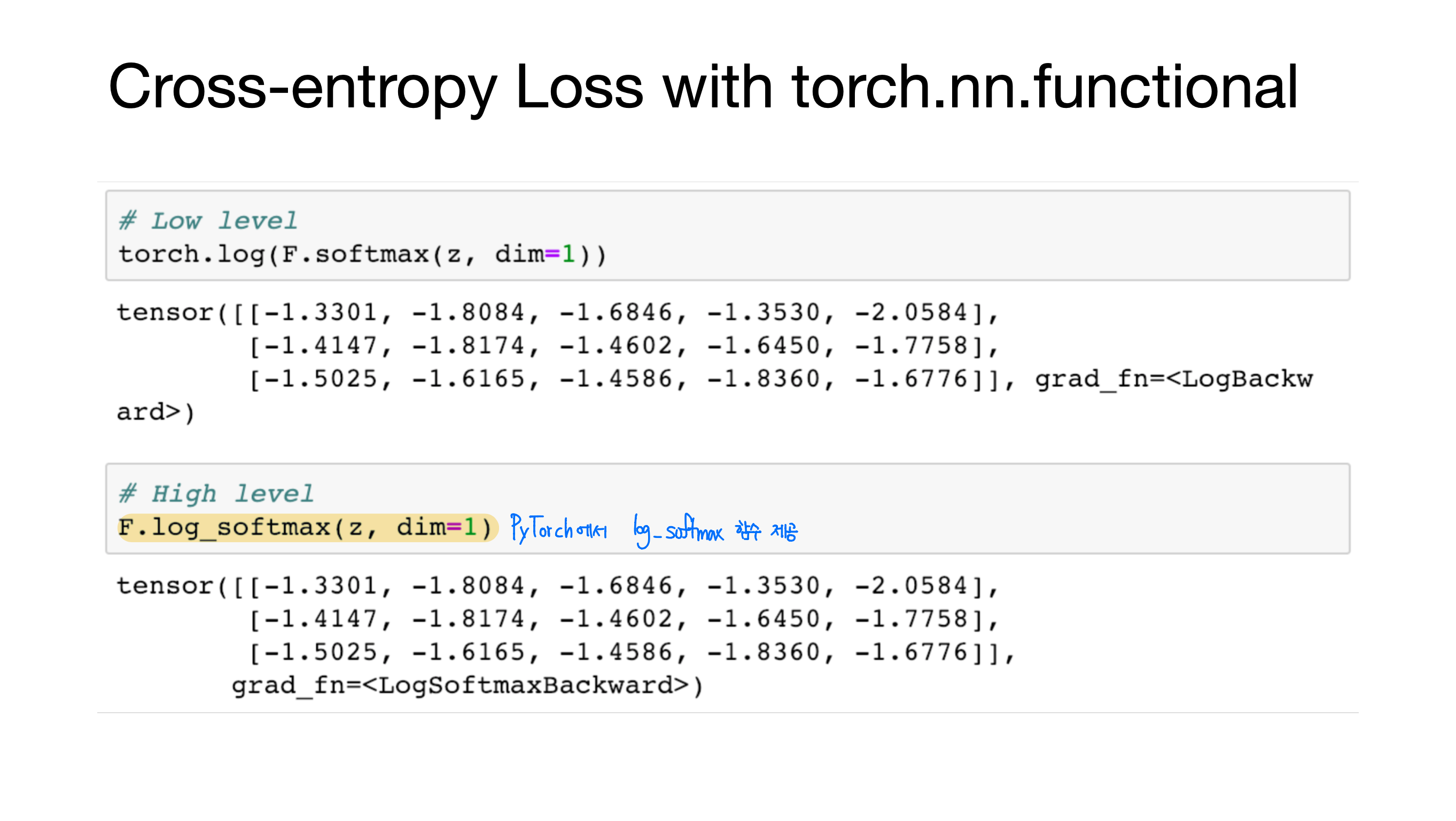
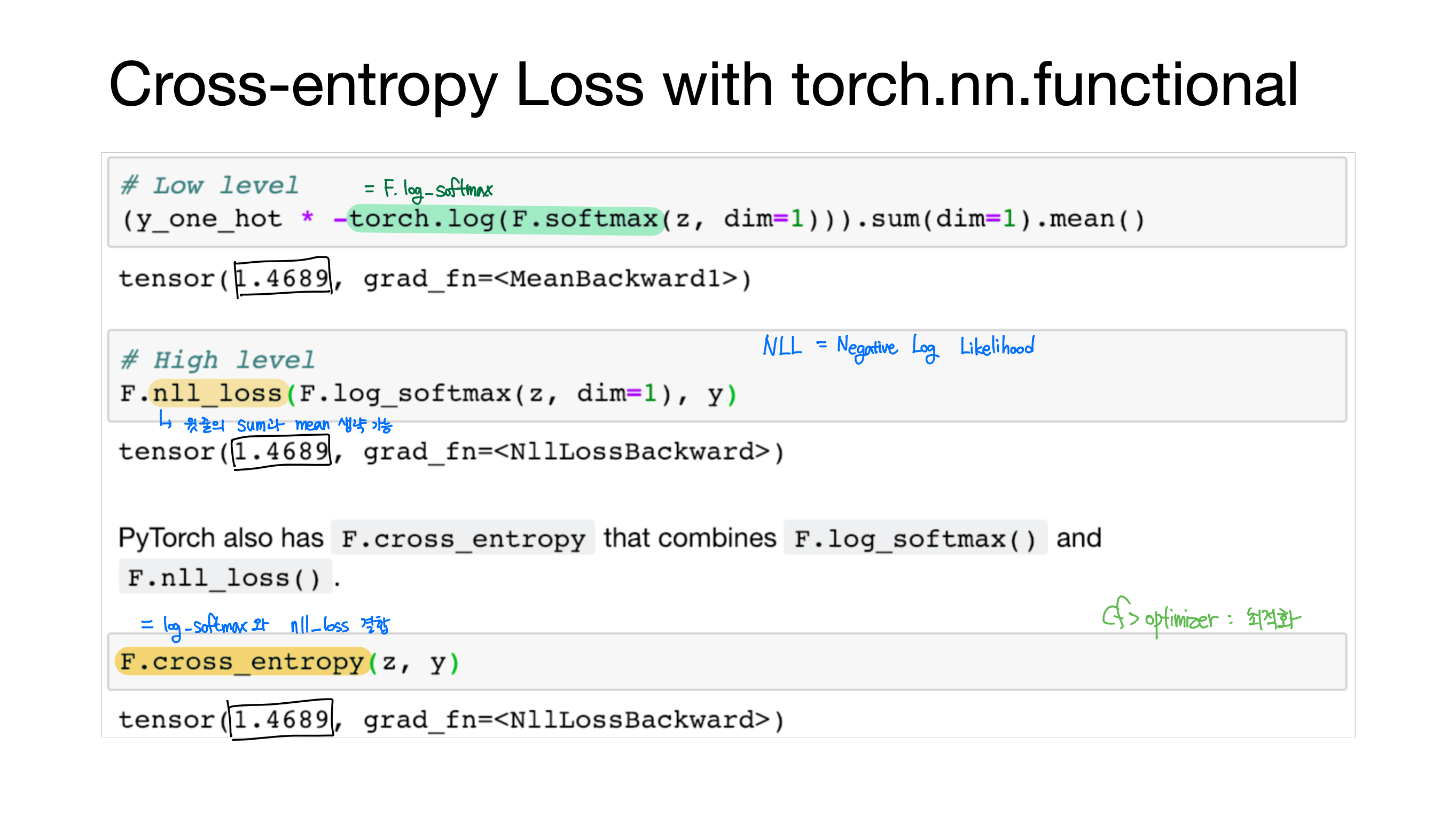
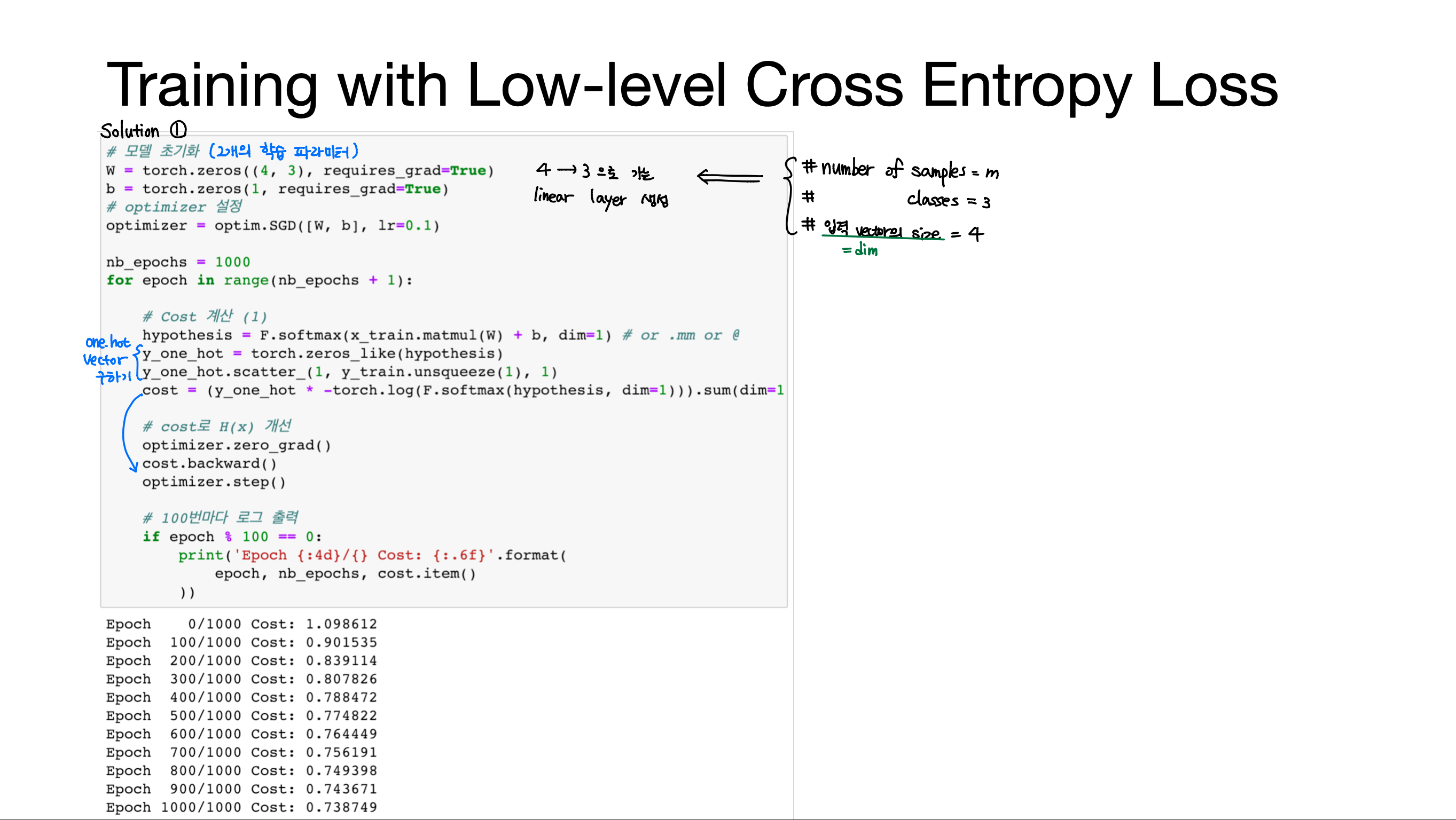
[Lab-06] Softmax Classification