동적계획법 (Dynamic Programming)이란

동적 계획법이란 매우 간단한 원리를 갖고 있다.

1. 주어진 문제를 여러 개의 하위 문제로 나누어 풀고
2. 하위 문제들의 해결 방법을 결합하여
3. 최종 문제를 해결한다.

다이내믹 프로그래밍은 다음 두 가지 가정이 만족하는 조건에서 사용할 수 있다.

1. 큰 문제를 작은 문제로 나눌 수 있고, 이 작은 문제들이 중복된다.
2. 작은 문제에서 구한 정답은 그것을 포함하는 큰 문제에서도 같다. 즉, 작은 문제에서 구한 정답을 큰 문제에서도 사용
   할 수 있다.

---

예시

Recursion

function fib(n) {
	if(n <= 2) return 1;
	return fib(n - 1) + fib(n - 2);
}

아래 두가지 예시는 DP의 개념을 활용한 예시

Recursion + Memoization

function fibMemo(n, memo = []) {
    if(memo[n] !== undefined) return memo[n];
		// 이미 해결한 하위 문제인지 찾아본다
    if(n <= 2) return 1;
    let res = fibMemo(n-1, memo) + fibMemo(n-2, memo);
		// 없다면 재귀로 결과값을 도출하여 res 에 할당
    memo[n] = res;
		// 추후 동일한 문제를 만났을 때 사용하기 위해 리턴 전에 memo 에 저장
    return res;
}

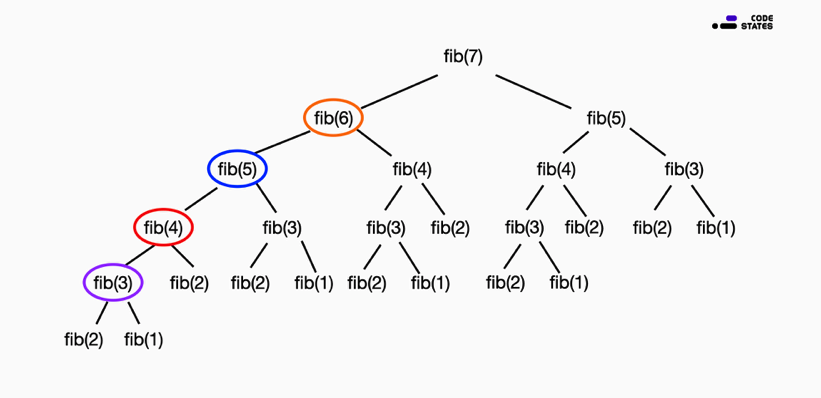
실제로 연산을 한 것은 왼쪽 4개뿐이며, 나머지는 왼쪽 4개에서 나온 값을 가져다 쓴 것 뿐이다.

Iteration + Tabulation

function fibTab(n) {
    if(n <= 2) return 1;
    let fibNum = [0, 1, 1];
		// n 이 1 & 2일 때의 값을 미리 배열에 저장해 놓는다
    for(let i = 3; i <= n; i++) {
        fibNum[i] = fibNum[i-1] + fibNum[i-2];
		// n >= 3 부터는 앞서 배열에 저장해 놓은 값들을 이용하여
		// n번째 피보나치 수를 구한 뒤 배열에 저장 후 리턴한다 
    }
    return fibNum[n];
}