Complexity

Big-O 표기법

시간 복잡도를 표기하는 방법은

• Big-O
• Big-Ω
• Big-θ

가 있다. 이 표기법들은 순서대로, 최악/최선/평균의 경우 입력값 증가에 따라, 시간 복잡도가 얼마나 증가하는지 표기하는 방법이다.

그러나 모든 edge케이스를 포함하는 Big-O 표기법, 즉 최악의 경우를 고려하는 표기법을 주로 사용한다.

O(1)

function O_1_algorithm(arr, index) {
	return arr[index];
}

let arr = [1, 2, 3, 4, 5];
let index = 1;
let result = O_1_algorithm(arr, index);
console.log(result); // 2

위 코드에서 arr의 길이에 상관 없이 즉시 index로 접근하여 값을 반환 할 수 있다.

O(n)

function O_n_algorithm(n) {
	for (let i = 0; i < n; i++) {
	// do something for 1 second
	}
}

function another_O_n_algorithm(n) {
	for (let i = 0; i < 2n; i++) {
	// do something for 1 second
	}
}

for문처럼 모든 요소에 접근 할 때, O(n)의 시간 복잡도를 가진다.

위 예시에서 아래/위 예시가 모두 O(n)인 이유는 Big-O에서 모든 차수와 계수는 무시되기 때문이다.
예를 들어서 n^3인 식이 있어도 n^2로 표기한다.

---

O(log n)

이진 탐색 트리를 생각하면 된다.
반복연산을 할 때마다 요소의 개수가 특정 수에 의해 나눗셈 연산이 시행될 때, O(log n)이라고 생각하면 된다.

예시로는 BST가 있다.

---

O(n^2)

function O_quadratic_algorithm(n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
		// do something for 1 second
		}
	}
}

function another_O_quadratic_algorithm(n) {
	for (let i = 0; i < n; i++) {
		for (let j = 0; j < n; j++) {
			for (let k = 0; k < n; k++) {
			// do something for 1 second
			}
		}
	}
}

위 예시에서 n^2, n^3, n^5 모두 Big-O에서는 O(n^2) 으로 포기한다. n이 커지면서 지수가 주는 영향력이 점점 퇴색 된다고 한다.

O(2^n)

Big-O표기법 중 가장 느린 시간 복잡도를 가진다.

function fibonacci(n) {
	if (n <= 1) {
		return 1;
	}
	return fibonacci(n - 1) + fibonacci(n - 2);
}

피보나치 수열을 재귀로 구현 했을 때, O(n^2)시간 복잡도를 가진 알고리즘이다.

---

Big-O 표기법을 코딩테스트에 이용하기

문제의 조건에 주어진 데이터의 제한을 보고 코딩에 필요한 시간 복잡도를 대략적으로 예측 할 수 있다.
이 표를 참고하자.

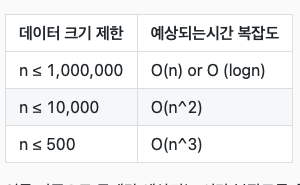
참고 공간복잡도/시간복잡도 상한

시간복잡도

데이터가 천만개면 80메가바이트다.
대부분 코딩테스트는 125,256,512이므로 천만개 이상부터는 고려해야한다.

시간 복잡도

연산의 상한은 1억번이라고 생각하자
예를 들어서
N = 100이면
O(N^3) => 100만번이므로 사용해도 되는 방법.