Permutation Sequence - LeetCode
★다시 풀어봐야할 문제★ ( 풀긴 풀었는데 시간초과 간당간당 )
접근 방법 [필수 작성]

- 9! = 98. . .21 = 362,880 < 2^19
- 완전탐색 가능
- 문자를 받는지, 숫자를 받는지 잘 구분하는 것이 중요!
아이디어
아이디어1: count 를 활용한다!
아이디어2: 다 구해놓고 k번째 원소를 return 한다! (nlogn → 19*362,880 = 700만) → 훨 쉽지만 연산 더 들어감 → 시간초과
코드 구현 [필수 작성]
완전탐색을 활용한 구현, 그러나 count 를 활용해서 발견하자마자 멈춤
# 5시 시작 -> 5시25분 끝
class Solution:
def getPermutation(self, n: int, k: int) -> str:
num_list = [i for i in range(1,n+1)]
permut_seq = []
stack = ""
count = 0
def backtrack():
nonlocal num_list
nonlocal stack
nonlocal permut_seq
nonlocal count
if len(stack) == n:
count += 1
permut_seq.append(stack[:])
return
for i in range(n):
if str(num_list[i]) not in stack:
stack += str(num_list[i])
backtrack()
stack = stack[:-1]
if count == k:
return
backtrack()
#print(permut_seq)
return permut_seq[-1]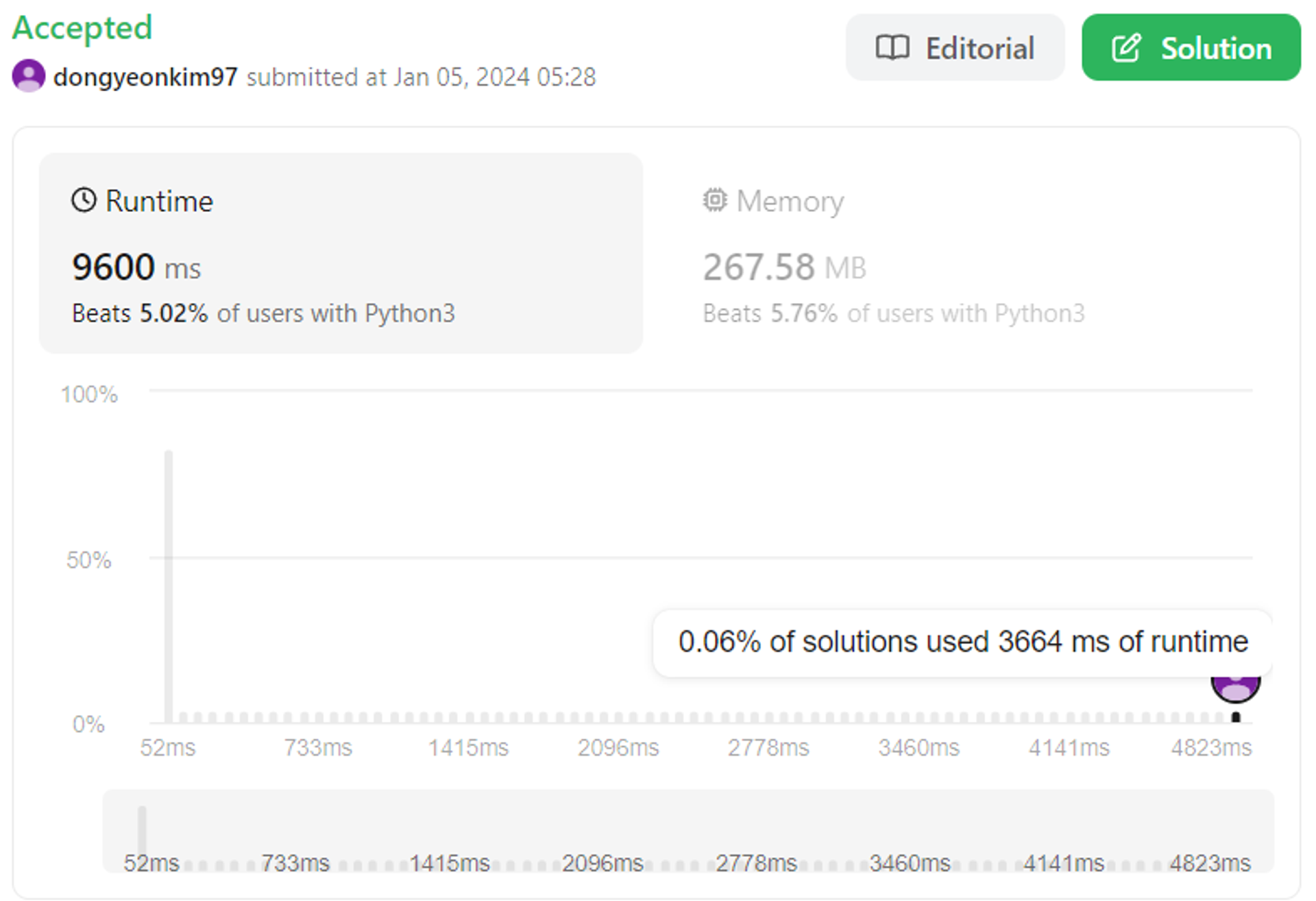
통과는 통과인데 거의 최적화 수준 꼴찌, 어떨때는 시간초과로 실패 → 과제 듀라 나중에 더 생각
Itertools 를 활용한 구현
한줄로 끝나는게… 인상적….
# 5시 시작 -> 5시25분 끝
from itertools import permutations
class Solution:
def getPermutation(self, n: int, k: int) -> str:
return "".join(map(str,list(permutations(range(1,n+1)))[k-1]))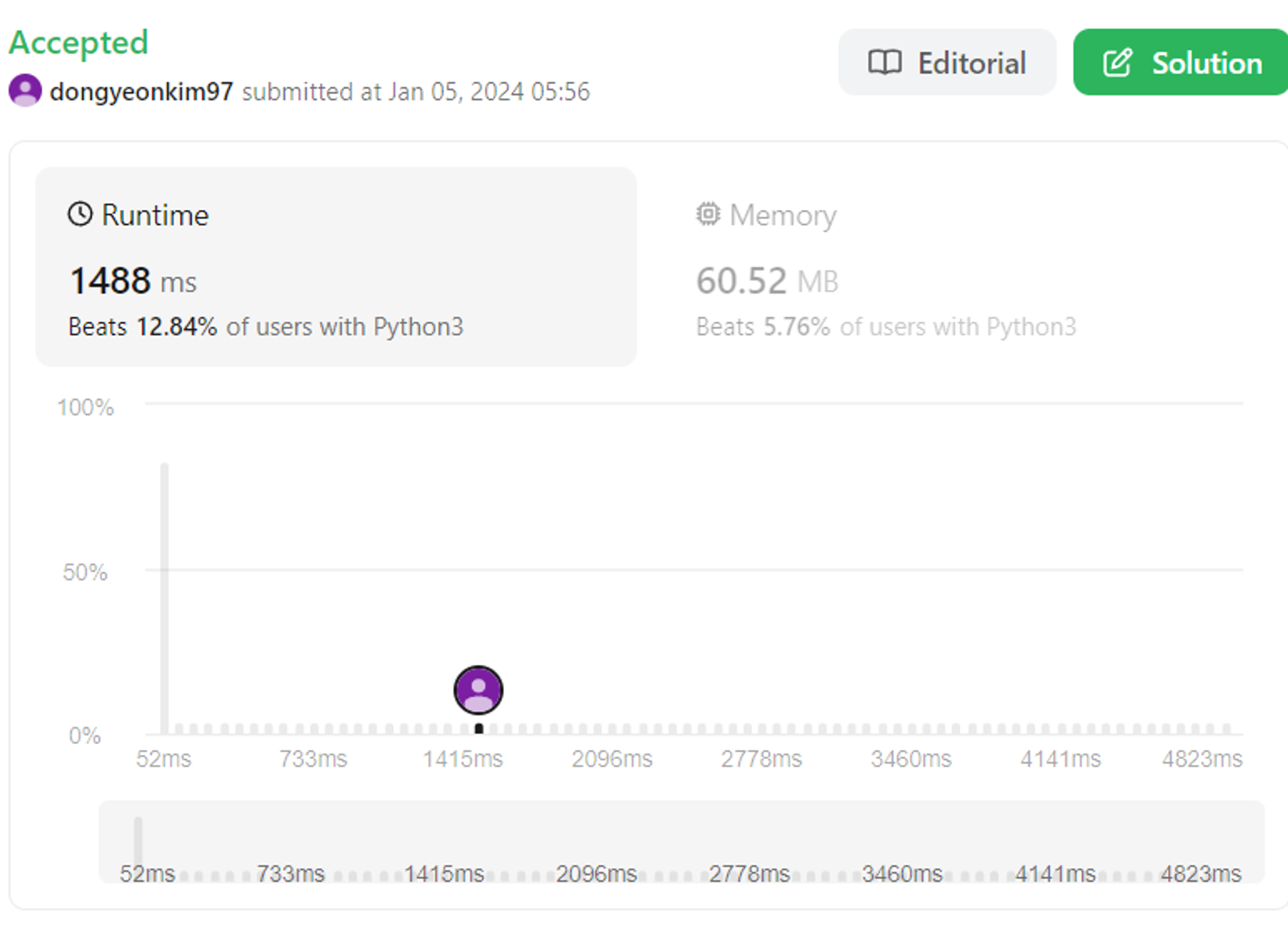
순열의 특징을 활용한 구현 → 듀 때문에 나중에 다시 구현
배우게 된 점 [ 필수 X ]
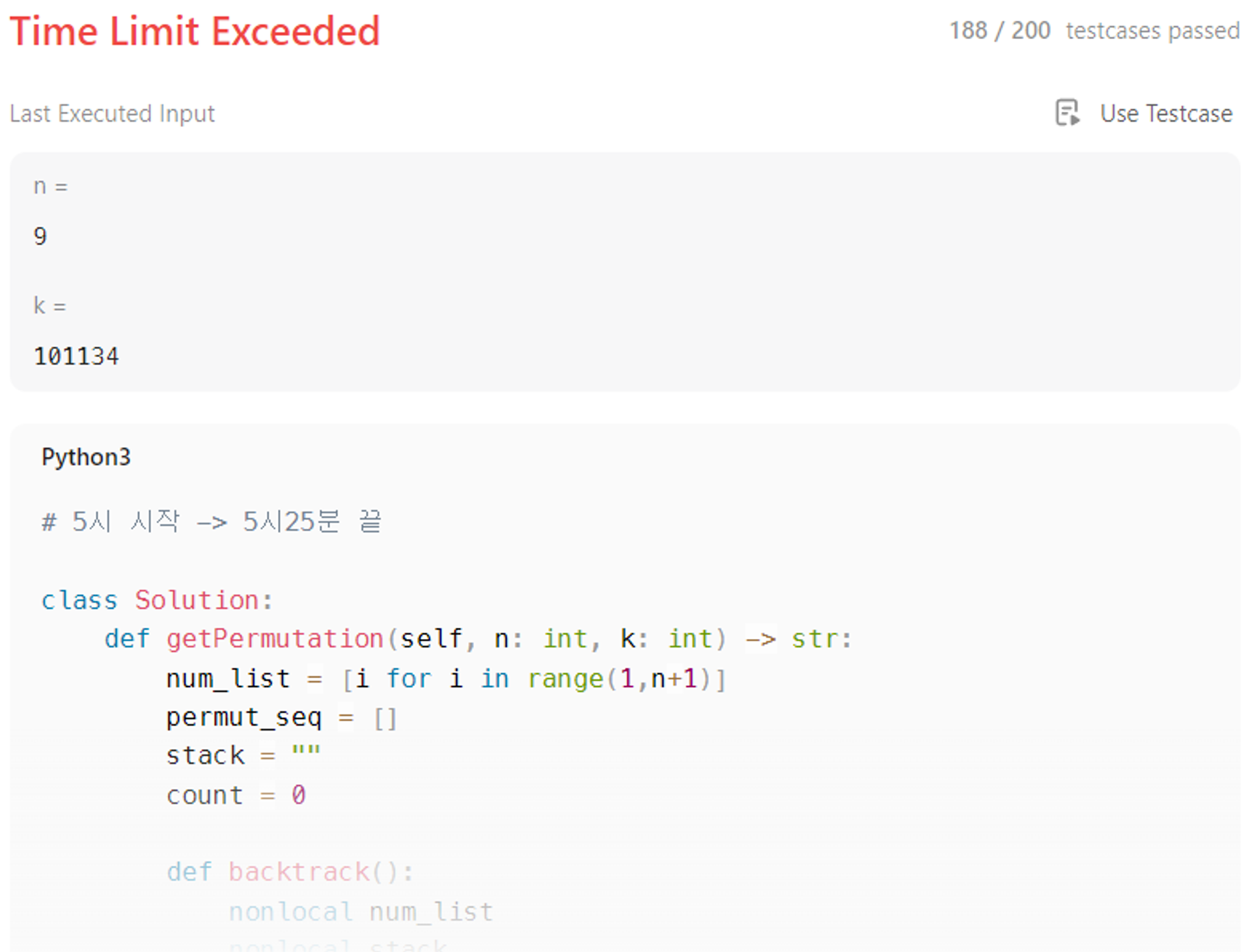
시간초과
n = 9, k = 136371
# 5시 시작 -> 5시25분 끝
class Solution:
def getPermutation(self, n: int, k: int) -> str:
num_list = [i for i in range(1,n+1)]
permut_seq = []
stack = ""
def backtrack():
nonlocal num_list
nonlocal stack
nonlocal permut_seq
if len(stack) == n:
permut_seq.append(stack[:])
return
for i in range(n):
if str(num_list[i]) not in stack:
stack += str(num_list[i])
backtrack()
stack = stack[:-1]
backtrack()
#print(permut_seq)
return permut_seq[k-1]재귀호출은 반복문호출보다 오버헤드가 더 크다!
Permutation 을 재귀로 구현할때와 반복문으로 구현할때 로직이 같다하더라도 재귀구현이 함수호출이 잦기 때문에 오버헤드가 더 큰 특징(시간이 더걸림)을 가진다.
9600ms(재귀) → 1488ms(반복문) → 48ms(순열특징활용)
ㅎㄷㄷ . . .
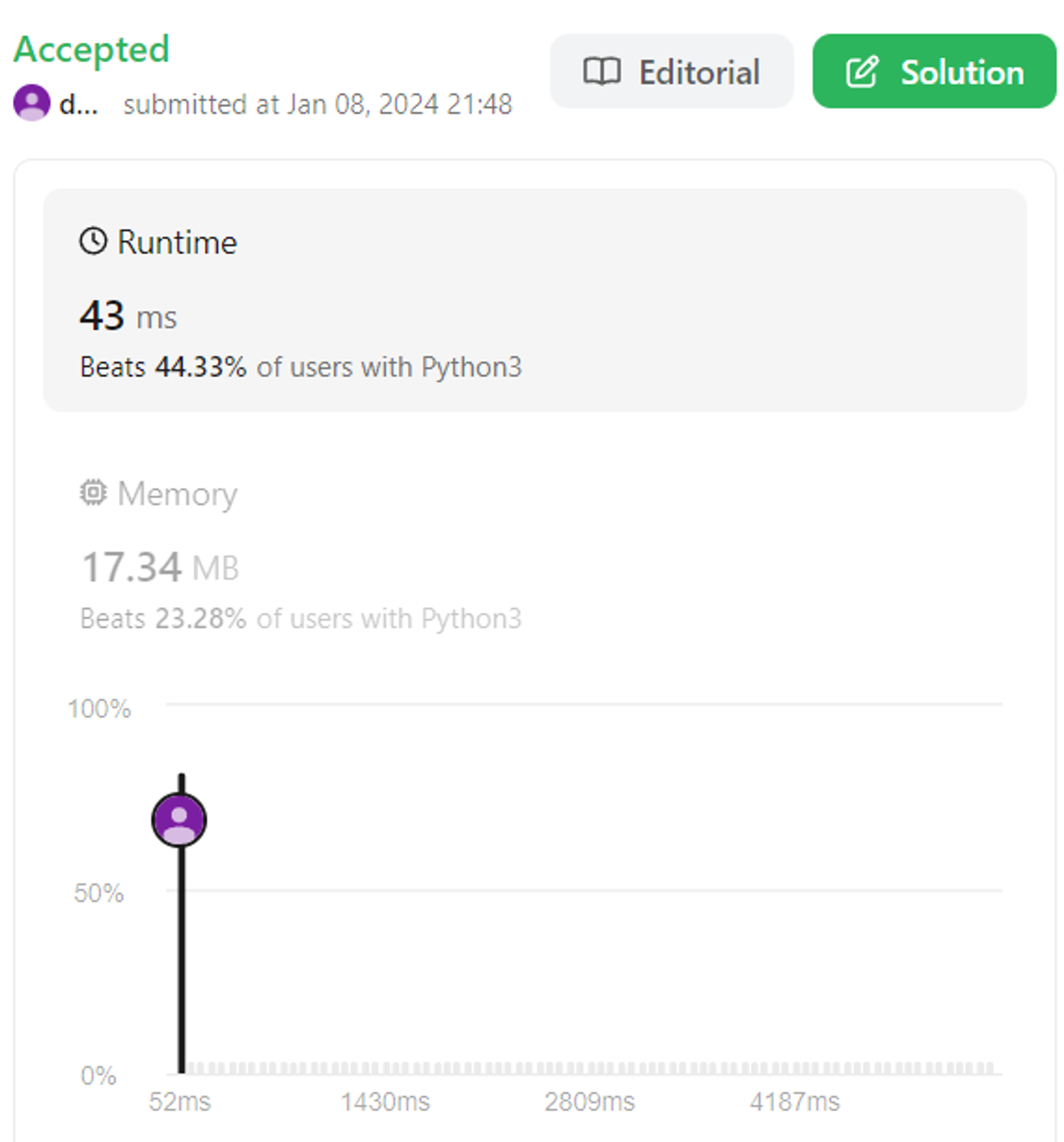
특정원소의 순차적 접근시, 순열의 수학적 특징을 활용하면 엄청난 시간효율성을 이끌어낼 수 있다.
질문 [ 필수 X ]
Q1
통과는 통과인데 거의 최적화 수준 꼴찌, 어떨때는 시간초과로 실패 → 과제 듀라 나중에 더 생각
시간초과도 의문이긴한데, 돌릴때마다 통과/실패가 다를 수도 있나?? 같은 로직으로 전개되는 것이 아닌가?? → 아슬하게 통과되고 안되고 차이인것 같다.. → 사실상 틀린거나 마찬가지..
Q2
“문제 조건을 잘 분석한다면 완전 탐색으로도 통과를 할 수 있음을 알려드리기 위함”
→ 효율성을 생각하지 않고, 모든 완전탐색 연산을 하여도 9! 의 연산수여서 시간초과가 나지 않고 통과해야하지 않나요?
Q3
“앞서 알려드린 방법대로 작성하신다면 적절한 실행 시간 내로 통과가 되는 것을 확인하실 수 있을겁니다.”
→ #여기서부터 새로 추가 / #여기까지 새로 추가 부분을 통해 알려드린 방법으로 구현했습니다.
# 5시 시작 -> 5시25분 끝
class Solution:
def getPermutation(self, n: int, k: int) -> str:
num_list = [i for i in range(1,n+1)]
permut_seq = []
stack = ""
count = 0
def backtrack():
nonlocal num_list
nonlocal stack
nonlocal permut_seq
nonlocal count
#print("===========================")
#print("function call")
#print("현재 permut_seq는 ",permut_seq)
if len(stack) == n:
#print("premut_seq에 "+stack+"을 추가후 다음 탐색으로 이동")
count += 1
permut_seq.append(stack[:])
return
for i in range(n):
if str(num_list[i]) not in stack:
#print("stack에 "+str(num_list[i])+"를 추가, 현재스택:",stack)
stack += str(num_list[i])
backtrack()
#여기서부터 새로 추가
if count == k:
#print("만약 이미 현재 permut_seq 길이가 "+str(k)+"이면 멈춤")
#print("permut_seq의 길이: "+str(len(permut_seq)))
return
#여기까지 새로 추가
#print("stack에서 "+str(num_list[i])+"를 제거 현재스택:",stack)
stack = stack[:-1]
backtrack()
##print(permut_seq)
return permut_seq[-1]===========================
function call
현재 permut_seq는 []
stack에 1를 추가, 현재스택:
===========================
function call
현재 permut_seq는 []
stack에 2를 추가, 현재스택: 1
===========================
function call
현재 permut_seq는 []
stack에 3를 추가, 현재스택: 12
===========================
function call
현재 permut_seq는 []
stack에 4를 추가, 현재스택: 123
===========================
function call
현재 permut_seq는 []
premut_seq에 1234을 추가후 다음 탐색으로 이동
stack에서 4를 제거 현재스택: 1234
stack에서 3를 제거 현재스택: 123
stack에 4를 추가, 현재스택: 12
===========================
function call
현재 permut_seq는 ['1234']
stack에 3를 추가, 현재스택: 124
===========================
function call
현재 permut_seq는 ['1234']
premut_seq에 1243을 추가후 다음 탐색으로 이동
stack에서 3를 제거 현재스택: 1243
stack에서 4를 제거 현재스택: 124
stack에서 2를 제거 현재스택: 12
stack에 3를 추가, 현재스택: 1
===========================
function call
현재 permut_seq는 ['1234', '1243']
stack에 2를 추가, 현재스택: 13
===========================
function call
현재 permut_seq는 ['1234', '1243']
stack에 4를 추가, 현재스택: 132
===========================
function call
현재 permut_seq는 ['1234', '1243']
premut_seq에 1324을 추가후 다음 탐색으로 이동
stack에서 4를 제거 현재스택: 1324
stack에서 2를 제거 현재스택: 132
stack에 4를 추가, 현재스택: 13
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324']
stack에 2를 추가, 현재스택: 134
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324']
premut_seq에 1342을 추가후 다음 탐색으로 이동
stack에서 2를 제거 현재스택: 1342
stack에서 4를 제거 현재스택: 134
stack에서 3를 제거 현재스택: 13
stack에 4를 추가, 현재스택: 1
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342']
stack에 2를 추가, 현재스택: 14
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342']
stack에 3를 추가, 현재스택: 142
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342']
premut_seq에 1423을 추가후 다음 탐색으로 이동
stack에서 3를 제거 현재스택: 1423
stack에서 2를 제거 현재스택: 142
stack에 3를 추가, 현재스택: 14
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342', '1423']
stack에 2를 추가, 현재스택: 143
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342', '1423']
premut_seq에 1432을 추가후 다음 탐색으로 이동
stack에서 2를 제거 현재스택: 1432
stack에서 3를 제거 현재스택: 143
stack에서 4를 제거 현재스택: 14
stack에서 1를 제거 현재스택: 1
stack에 2를 추가, 현재스택:
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342', '1423', '1432']
stack에 1를 추가, 현재스택: 2
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342', '1423', '1432']
stack에 3를 추가, 현재스택: 21
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342', '1423', '1432']
stack에 4를 추가, 현재스택: 213
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342', '1423', '1432']
premut_seq에 2134을 추가후 다음 탐색으로 이동
stack에서 4를 제거 현재스택: 2134
stack에서 3를 제거 현재스택: 213
stack에 4를 추가, 현재스택: 21
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342', '1423', '1432', '2134']
stack에 3를 추가, 현재스택: 214
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342', '1423', '1432', '2134']
premut_seq에 2143을 추가후 다음 탐색으로 이동
stack에서 3를 제거 현재스택: 2143
stack에서 4를 제거 현재스택: 214
stack에서 1를 제거 현재스택: 21
stack에 3를 추가, 현재스택: 2
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342', '1423', '1432', '2134', '2143']
stack에 1를 추가, 현재스택: 23
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342', '1423', '1432', '2134', '2143']
stack에 4를 추가, 현재스택: 231
===========================
function call
현재 permut_seq는 ['1234', '1243', '1324', '1342', '1423', '1432', '2134', '2143']
premut_seq에 2314을 추가후 다음 탐색으로 이동
만약 이미 현재 permut_seq 길이가 9이면 멈춤
permut_seq의 길이: 9
만약 이미 현재 permut_seq 길이가 9이면 멈춤
permut_seq의 길이: 9
만약 이미 현재 permut_seq 길이가 9이면 멈춤
permut_seq의 길이: 9
만약 이미 현재 permut_seq 길이가 9이면 멈춤
permut_seq의 길이: 9실제 동작도 의도대로 count 가 k와 동일할때 모든 재귀문을 빠져나와 비효율이 발생하지 않는 것으로 확인됩니다. 하지만, 여전히 시간효율을 간당간당하거나 통과하지 못하거나 인것 같습니다…
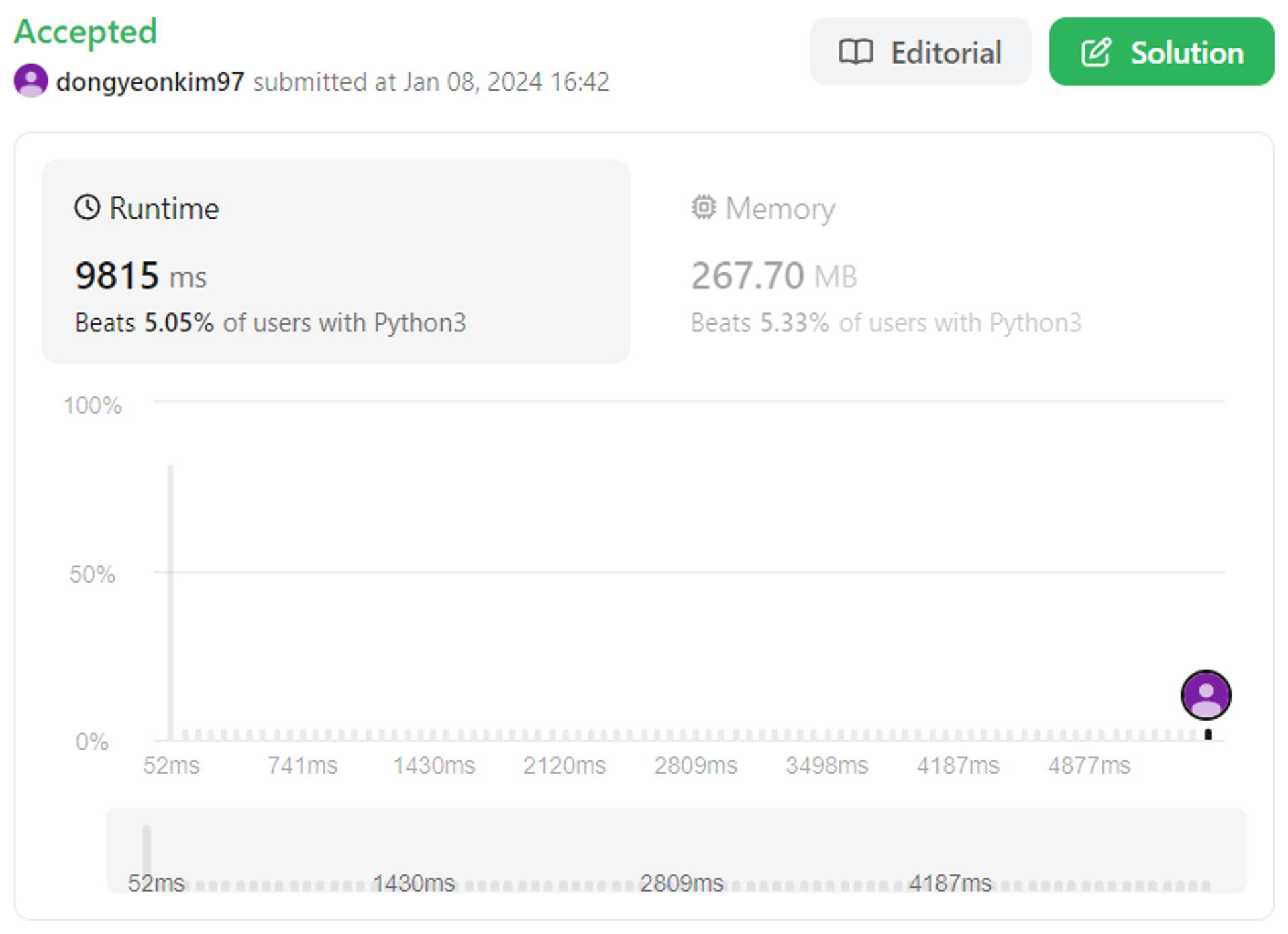
Q4
class Solution:
def getPermutation(self, n: int, k: int) -> str:
return "".join(map(str,list(permutations(range(1,n+1)))[k-1]))위의 두번째 풀이 코드 같은 경우 모든 순열케이스를 생성한 후, k-1 번째를 반환하는 것인데, 이 방법은 9! 모든 경우를 계산 후, k-1 번째를 반환하는 비효율적인 방법과 같습니다. 하지만 Untitled 여기서 보면 아시다시피, 시간효율이 훨씬 향상됐음을 보여줍니다. Q2,Q3 과 함께 혼동이 오는 부분입니다.
피드백 [ 코치 작성 ]
이 문제에서 요구하는 정확한 해결 방법은 모든 순열을 구하고 k번째 순열을 구하는 것이 아닌 앞에서 부터 차례대로 k번째 순열을 구하는 것입니다. 이러한 방법은 k+1번째 이후의 순열을 구하지 않으며 그렇기에 기존에 작성하신 방법과 실행시간에서 큰 차이가 발생합니다.(n=9, k=1인 경우 모든 순열을 구하기 위해 9!의 실행 시간을 갖지만 앞에서부터 구하면 1의 시간을 갖습니다.)
이 문제를 과제로 드린 이유에는 문제 조건을 잘 분석한다면 완전 탐색으로도 통과를 할 수 있음을 알려드리기 위함이며 앞서 알려드린 방법대로 작성하신다면 적절한 실행 시간 내로 통과가 되는 것을 확인하실 수 있을겁니다.
추가 질문 답변
A2 & A4
효율성을 고려하지 않고 모든 경우를 완전 탐색을 할 경우 시간 복잡도를 고려한다면 시간 초과가 발생하지 않고 통과하는게 일반적으로는 맞습니다. 그렇기에 itertool을 활용한 예제의 정답 코드가 통과를 할 수 있는 것이고요. 하지만 재귀 함수의 경우 이야기가 달라집니다. 함수는 호출하는 행위 자체에 소요가 필요합니다. 이러한 소요 자원들을 통칭하여 오버헤드라고 부릅니다. 재귀 함수의 경우 함수 호출 과정이 자주 발생하기에 이런 오버 헤드가 자주 발생하게 됩니다. 그렇기에 재귀 함수의 경우 잦은 오버 헤드의 발생이 실행 시간을 지연시켜 통과하지 못하는 경우가 생기는 것입니다.(itertool은 내부적으로 반복문으로 구현되어있습니다.)
A3
해당 방법은 최적의 과정이 아닙니다. 예제 코드의 경우 순열의 규칙을 찾아 자릿수 한 개의 값을 찾기 위해 n번째 자릿수의 값을 찾는 과정에서는 (n-1)!으로 나눈 몫과 나머지를 통해 계산하고 있습니다. 즉 한 개의 자릿수를 찾기 위해 소요되는 연산은 (n-1)! 값을 계산하는 n-1, 나누기 연산을 하는 상수 시간만 소요되며 모든 자릿수를 찾는 과정 또한 이의 반복입니다. 그렇기에 조합을 앞에서 부터 1개씩 찾아가는 것과는 큰 실행 시간의 차이를 보이게 됩니다. 간단한 예제를 드리자면 n=9, k=362880으로 주어진 경우 예제 코드는 나누기 연산을 통해 실행 시간을 크게 줄일 수 있지만 앞에서 부터 찾는 경우 모든 순열을 구한 후 k번째를 찾는 것과 차이가 없어집니다.
