Network Delay Time
문제 파악 [필수 작성]
문제이해
특정 노드 k로 부터 전체 노드까지
다 퍼져나가는 최소시간을 구하는 문제
만약 다 퍼져나갈 수 없으면 -1 을 리턴
제한 조건 확인
노드는 최대 100개
엣지는 최대 6000개
자기자신을 가리키는 엣지는 없음
가중치는 0~100
중복엣지 없음
아이디어
전형적인 다익스트라 문제
while 문과 힙을 활용한 구현
우선 times 연결리스트를 (w,u,v) 순으로 바꿔주어야한다.
힙에서 최소인것부터 하나씩 뽑고,
만약 방문했던 노드면 그냥 pass
방문안했던 노드면 최소 가중치 업데이트 후 bfs 탐색 이어하기
시간복잡도
모든 노드에 대해 모든 엣지를 탐색해야하므로,
최대 O(E+V) -> 시간 충분
접근 방법 [필수 작성]
코드 구현 [필수 작성]
1차 시도(40분 소요)
한방에 통과
import heapq
import sys
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
result = 0
INF = sys.maxsize
min_heap = []
visited = [False for _ in range(n+1)]
visited[0] = True
node_weight = [INF for _ in range(n+1)]
node_weight[0] = 0
edges = {}
for time in times:
u,v,w = time
if u in edges:
edges[u].append([w,v])
else:
edges[u] = [[w,v]]
heapq.heappush(min_heap,[0,k])
while min_heap:
tw, tv = heapq.heappop(min_heap)
if visited[tv] == False:
visited[tv] = True
node_weight[tv] = tw
if tv in edges:
for edge in edges[tv]:
nw,nv = edge
heapq.heappush(min_heap,[tw+nw,nv])
for v in visited:
if v == False:
return -1
for w in node_weight:
result = max(result,w)
return result
2차 시도(최적화)
가중치 최대값을 찾기 위한 의미 없는 for을 지워주고 가중치가 업데이트 될때마다 최대값을 갱신하는 방식으로 변경 (연산시간의 유의미한 향상은 없음)
또 아래 파트를 추가적으로 개선하고 싶다.
if u in edges:
~~~
if tv in edges:
~~~아래와 같이 개선
if tv in edges:
for edge in edges[tv]:
>>>
for edge in edges.get(tv,[]):또는 해설코드 처럼 defaultdict 를 활용할 수도 있다.
graph = defaultdict(list)
for u, v, time in times:
graph[u].append((time, v))import heapq
import sys
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
result = 0
INF = sys.maxsize
min_heap = []
visited = [False for _ in range(n+1)]
visited[0] = True
node_weight = [INF for _ in range(n+1)]
node_weight[0] = 0
edges = {}
for time in times:
u,v,w = time
if u in edges:
edges[u].append([w,v])
else:
edges[u] = [[w,v]]
heapq.heappush(min_heap,[0,k])
while min_heap:
tw, tv = heapq.heappop(min_heap)
if visited[tv] == False:
visited[tv] = True
node_weight[tv] = tw
result = max(result,tw)
for edge in edges.get(tv,[]):
nw,nv = edge
heapq.heappush(min_heap,[tw+nw,nv])
for v in visited:
if v == False:
return -1
return result배우게 된 점 [필수 작성]
에러코드해석
처음에 networkDelayTime 오류라길래 생전 처음보는 오류코드가 나와서 당황했었다. 모든 코드문제를 모의시험이라고 생각하고 풀기때문에 직접 검색해보지는 못하였고, 어떻게 해결할까 에러코드를 유심히 보았고, 딕셔러니에서 키값을 찾지 못할때 생기는 그냥 단순한 KeyError 였다.
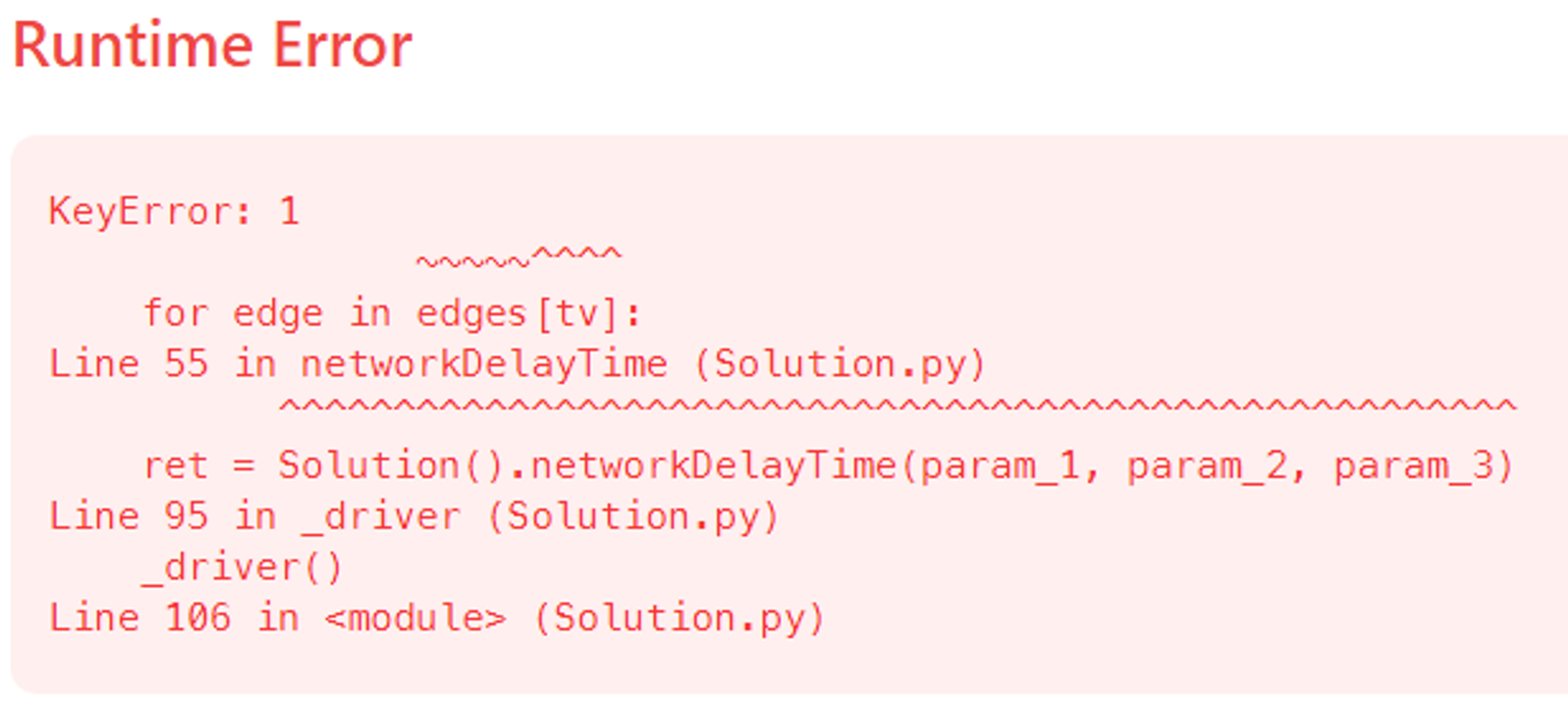
문제를 다 푼 후 해당 에러코드에 대해서 구글링 해보았는데, 해당 에러코드에 대한 마땅한 정보를 찾지 못했다. networkDelayTime 에러명은 리트코드에서 자체적으로 정의한 solution 함수 test함수 이름인건가? 궁금증이 생긴다. → 아!!! 문제이름 자체가 networkDelayTime 이군요…
까다로웠던 점
노드 번호가 0 부터 시작하지 않고 1부터 N까지 주어진 점
최대 연산수를 계산하기 위해 처음부터 끝까지 다시 max함수를 적용하여야 했던점 → weight 최대치가 업데이트될때마다로 최적화
질문 [ 필수 X ]
Q1. 에러코드해석
networkDelayTime 의 의미가 궁금합니다.
→ 아!!! 문제이름 자체가 networkDelayTime 이군요… 질문하고나서 해설강의를 보려다 제목보고 알았습니다.
Q2. [모든 노드에 대해 모든 엣지를 탐색해야하므로,
최대 O(E+V) -> 시간 충분](https://www.notion.so/O-E-V-46b16e58c0e744e8b9e4e18fc70da5fa?pvs=21)
시간 복잡도 계산이 맞는지 궁금합니다.
Q2 에 대한 집중 토론 및 연구 정리
실시간 디스코드 피드백 후 Q3에 대한 셀프 답변
먼저 E 는 최대 V^2 이므로, O(logE) → O(logV^2) → O(2logV) → O(logV) 로 간략화 될 수 있다.
우선 다익스트라 알고리즘의 핵심은 힙의 사용이다. 확장되서 새롭게 닿은 노드를 힙에서 뽑고 (VlogV), 해당 노드가 가진 간선을 통해서 그래프를 확장하고 (ElogV), 확장한 각 간선에 대해서 최단거리가 갱신(E) 되기 때문에 시간복잡도는 다음과 같다. 이때 힙의 크기가 초기에 V가 아님에도 불구하고 삽입삭제를 logV 라고 하는 이유는 최악의 연산시간을 상정(모든 노드가 힙에 삽입된 상태로 상정)하기 때문이다.
VlogV + ElogV + E → O((E+V)logV)
이는 다시 한번 아래에 의해 다음과 같이 간략화할 수 있다.
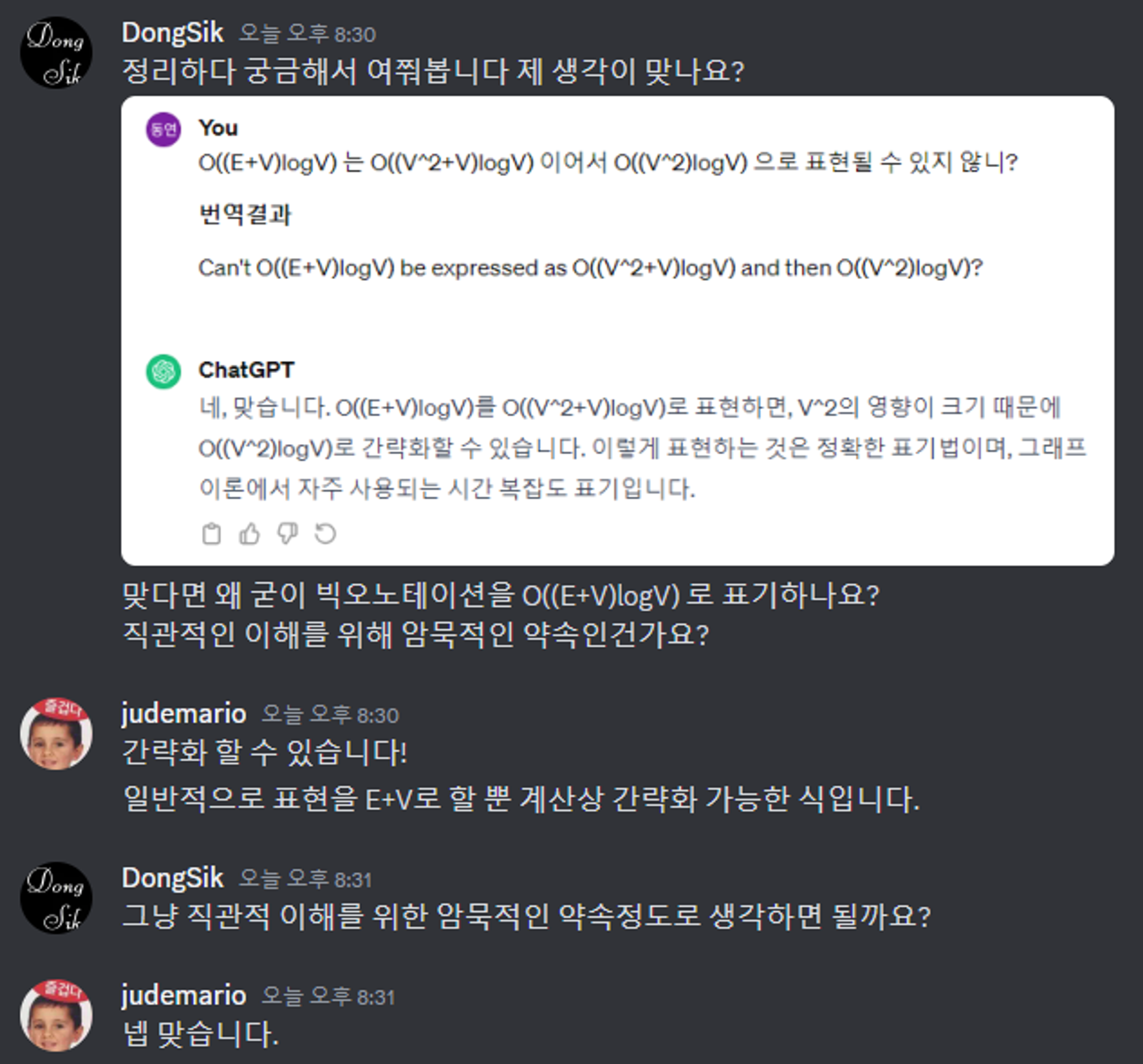
O((E+V)logV) → O((V^2+V)logV) → O((V^2)logV)
그렇다면 여기서 다시 의문점이 생길 수 있다.
O((V^2)logV) 는 기존의 힙을 사용하지 않은 다익스트라 알고리즘의 시간복잡도인 O(V^2) 보다 큰 것이 아닌가?
하지만 이는 Big-O 표기법의 특성에 의해서 생기는 문제이다.

E 가 최악의 경우 V^2 이지만, 대부분의 상황에서 Graph 는 Sparse 한 형태이며, 따라서 E가 V^2까지 되는 경우는 잘 없고, 보통 V에 비례한다고 생각할 수 있다. 그런 관점에서 heap을 사용하면, heap을 사용하지 않고, list만 사용한 경우보다 연산시간을 개선할 수 있다.
정리하면 아래와 같다. Ei 의 의미는 전체 간선수가 아닌, 각 노드의 간선수라는 의미이고 이는 최대 V-1 개이다.
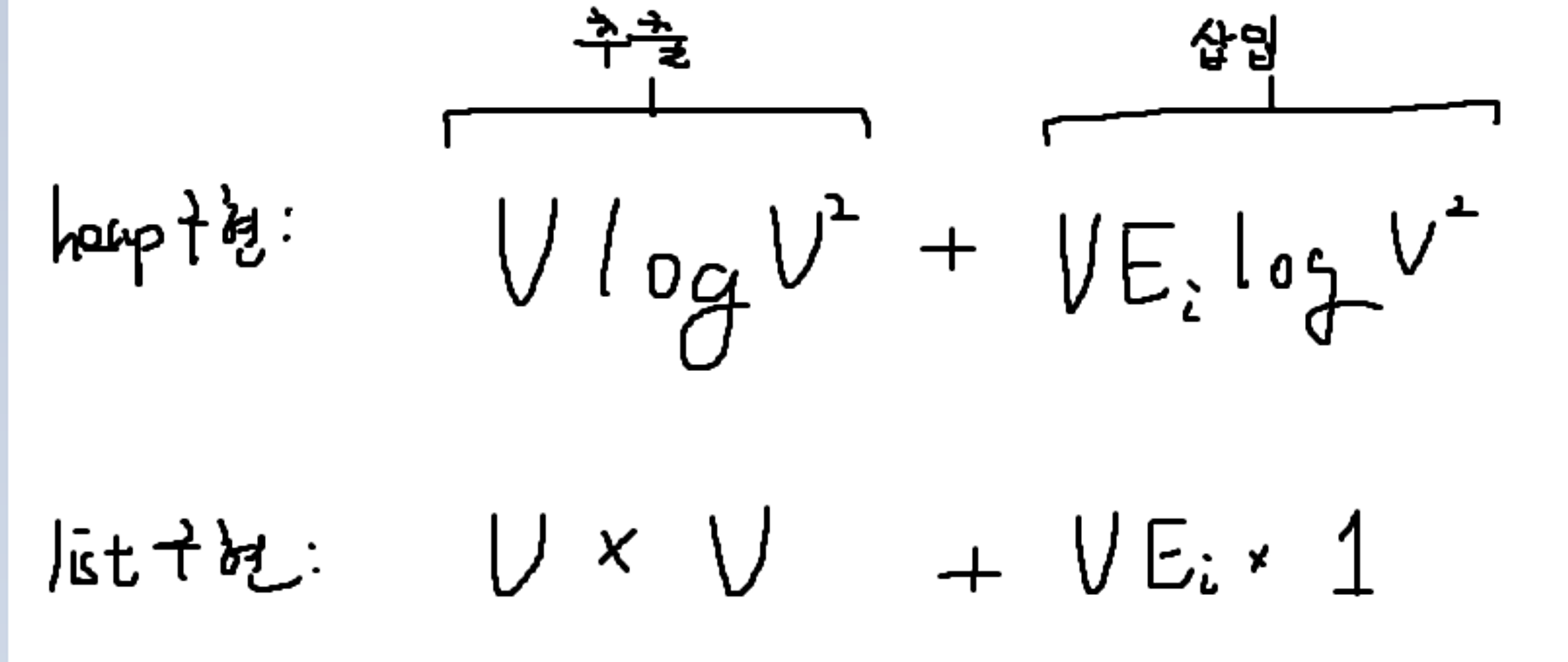
Q2 에 대한 코치님의 답변의 핵심은, 내가 짠 코드의 구현이 heap 내 이미 (10,4)와 같은 노드가 있을때, (8,4) 가 추가될때, (10,4)를 제거하고 (8,4)를 넣는게 아닌, 그냥 (8,4)를 넣었기 때문에, 통상적인 다익스트라 알고리즘의 방식과 다르다는 것을 말해주고 싶으셨다고 한다.
따라서 내 코드의 경우 엄밀히 말하면 시간복잡도는
O(Vlog(V+E)+ Elog(V+E) + E)이고
이는 다시 (V+E)log(V+E) → O((V^2)log(V)) 로 정리될 수 있다.
답변
A1.
A2.
다익스트라 알고리즘은 구현에 따라 시간 복잡도가 크게 달라집니다.
초기에 개발된 다익스트라 알고리즘은 O(V^2)의 시간 복잡도를 가졌으며 이후 개선된 다익스트라 알고리즘의 시간 복잡도는 각 노드에 대해 우선순위 큐에서 추출하는 VlogV, 각 간선에 대해 우선순위 큐에서 우선순위를 갱신하는 ElogV로 O((V+E)logV)의 시간 복잡도를 갖습니다.
동연님께서 구현하신 코드의 경우 우선순위 큐 내부의 노드의 우선순위를 갱신하는 것이 아닌 노드를 새로운 우선순위와 함께 우선순위 큐에 입력하는 방식으로 구현되어있습니다. 그렇기에 각 간선마다 매번 우선순위가 갱신된다면 우선순위에 들어가는 데이터의 양이 V+E, 우선순위에서 추출하는 시간은 log(V+E) 간선E는 V^2이하이므로 O(log(V+E)) = O(logV). 즉 O((V+E)logV)의 시간 복잡도를 갖는 것으로 보입니다.
