★trapping rain water 2★
★다시 풀어봐야할 문제★ (제출 눌렀는데 코너케이스 걸림, 코너케이스 못찾겠어서 결국 코너케이스 확인함, 해설코드 로직 차용함)
https://leetcode.com/problems/trapping-rain-water-ii/description/
문제 파악 [필수 작성]
문제이해
우물을 찾아라
제한 조건 확인
최대200x200
최소 1x1
최대 높이 2x10^4 -> 높이 직접 하나씩 일일이 세지 말라는 의미, 한번에 받아서 해라
아이디어
물이 차기 위한 조건? -> 사방이 다 막혀있어야함
200200 칸은 한개층당 40,000 칸
1층부터 순차적으로 채워나가면?
40,000 2 10^4 = 80,000 10,000 = 800,000,000 = 8억 시간 초과 -> 일일이 세지 마라
40000개의 칸을 위에서 부터 레이저를 쏴봄
내가 레이저 쏘는 칸 높이를 구하고
내가 쏘는칸 기준 4개 방향 높이 중 (아예 바깥은 0 임)
case1 : 내 칸보다 큰것만 있는경우
-> 내 칸보다 큰 것중 최소 높이 만큼은 최소한 물이 참 -> 그 이상은 더 찰수도 안찰수도 있음
case2 : 내칸보다 큰것도 있고, 같거나 작은것도 있는 경우
-> ??? 생각이 잘 안됨
case3 : 내칸보다 다 같거나 작은 경우
-> 해당 칸에는 물을 채울 수 없음
생각이 잘 안되서 이전 2D 문제에서 부터 아이디어 차용해서 디벨롭
그냥 2D 를 가로세로 겹겹이 해서 3D로 바꾸면 되는거 아닌가?
2D문제를 어떻게 풀었었지?
가로 한번
오른쪽 끝에서 한번 왼쪽끝에서 한번 시작
0번째부터 시작
현재까지 만난 높이중 가장 높은 높이 저장
만약 다음꺼 높이가 현재꺼 높이보다 작으면
해당 위치 물웅덩이는 min(해당위치 물웅덩이높이,현재꺼높이-다음꺼높이)
만약 다음꺼 높이가 현재꺼 높이보다 크면
만난 높이 중 가장 높은 높이 업데이트
반대쪽에서부터 동일하게 또 시작
현재까지 만난 높이중 가장 높은 높이 저장
만약 다음꺼 높이가 현재꺼 높이보다 작으면
해당 위치 물웅덩이는 min(해당위치 물웅덩이높이,현재꺼높이-다음꺼높이)
만약 다음꺼 높이가 현재꺼 높이보다 크면
만난 높이 중 가장 높은 높이 업데이트
세로도 동일하게 한번더
동일
다 끝나면 가로세로 서로 비교해서 더 낮은거 가 실제 물웅덩이 높이
시간복잡도
400x2(2D양방향슬라이드) x 200(가로한번) x 200(세로한번) + 전체순회 200x200
= O(800x200x200) = 32,000,000 = 3200만 간당하게 통과가능
자료구조
접근 방법 [필수 작성]
코드 구현 [필수 작성]
1차 시도(1시간 10분 소요)
어떤 코너케이스가 있을지 결과 안보고 안보고 생각중
→ 코너케이스 도저히 찾을 수 없어서 코너케이스 결과 봄
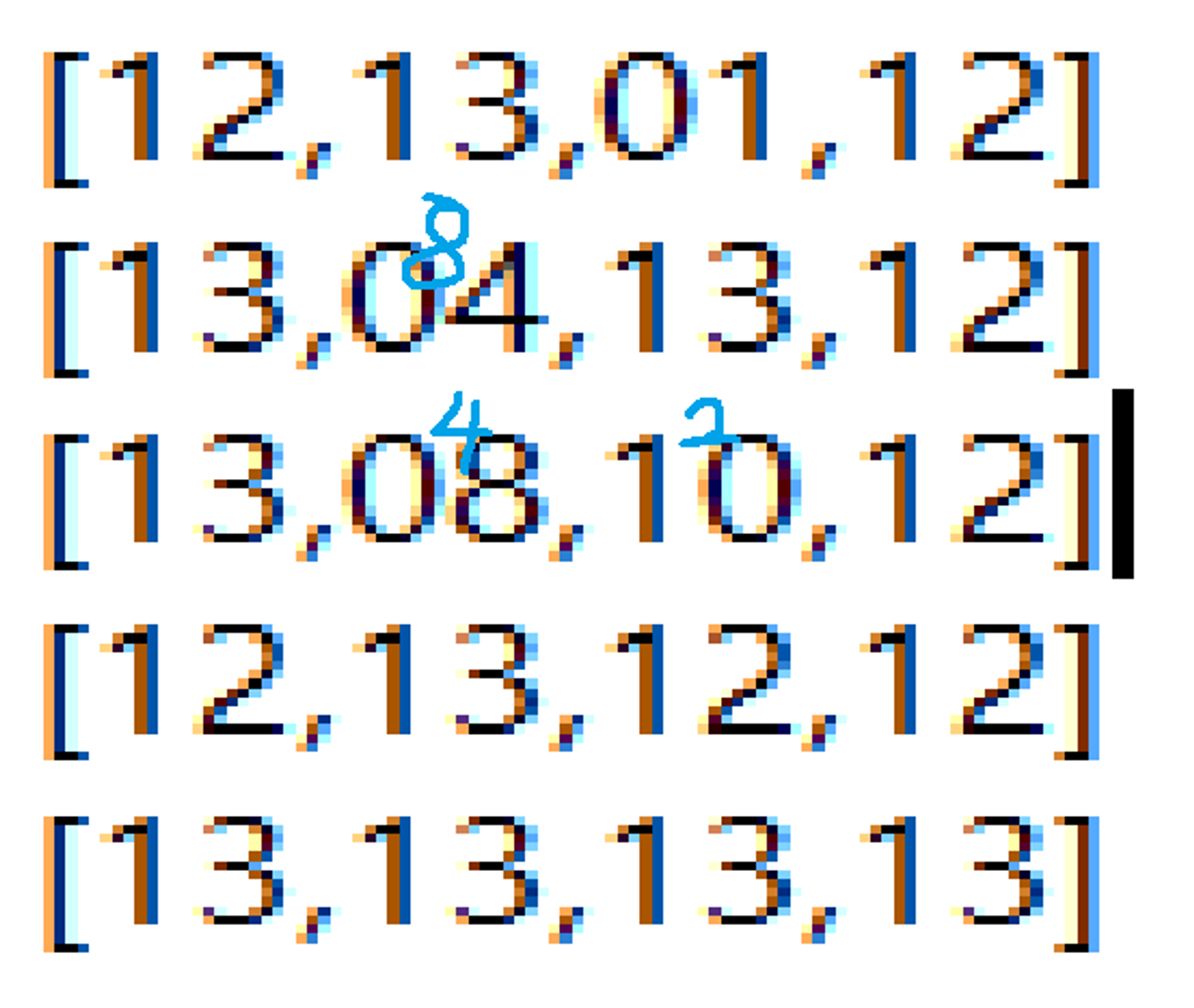
상하좌우만 보면 된다고 생각했고, 실제로 코드도 그 부분에 대해서는 다 맞게 동작하지만, 애초에 아이디어 및 로직 자체가 잘못됨. 물이라는 특성때문에 현재 노드에서 상하좌우만 보면될게 아니라, 내 상하좌우의 상하좌우까지도 신경써주어야함. 그리고 이게 계속 이어짐. 뭔가 이런 특성때문에 그래프적인 특성을 이용하는 아이디어를 떠올려야할것같다.
import sys
class Solution:
def trapRainWater(self, heightMap: List[List[int]]) -> int:
INF = sys.maxsize
def transpose(source_list):
source_list_T = []
for col in range(len(source_list[0])):
col_list = []
for row in range(len(source_list)):
col_list.append(source_list[row][col])
source_list_T.append(col_list)
return source_list_T
def raining(land_list):
water_list = [INF for _ in range(len(land_list))]
max_h = 0
for i in range(len(land_list)):
if land_list[i] < max_h:
water_list[i] = min(water_list[i],max_h-land_list[i])
elif land_list[i] > max_h:
max_h = land_list[i]
water_list[i] = 0
else:
water_list[i] = 0
max_h = 0
for ri in range(len(land_list)-1,-1,-1):
if land_list[ri] < max_h:
water_list[ri] = min(water_list[ri],max_h-land_list[ri])
elif land_list[ri] > max_h:
max_h = land_list[ri]
water_list[ri] = 0
else:
water_list[ri] = 0
return water_list
heightMap_T = transpose(heightMap)
garo_water_list = []
sero_water_list = []
for land in heightMap:
garo_water_list.append(raining(land))
for land in heightMap_T:
sero_water_list.append(raining(land))
sero_water_list = transpose(sero_water_list)
result = 0
for row in range(len(heightMap)):
for col in range(len(heightMap[0])):
result += min(garo_water_list[row][col], sero_water_list[row][col])
return result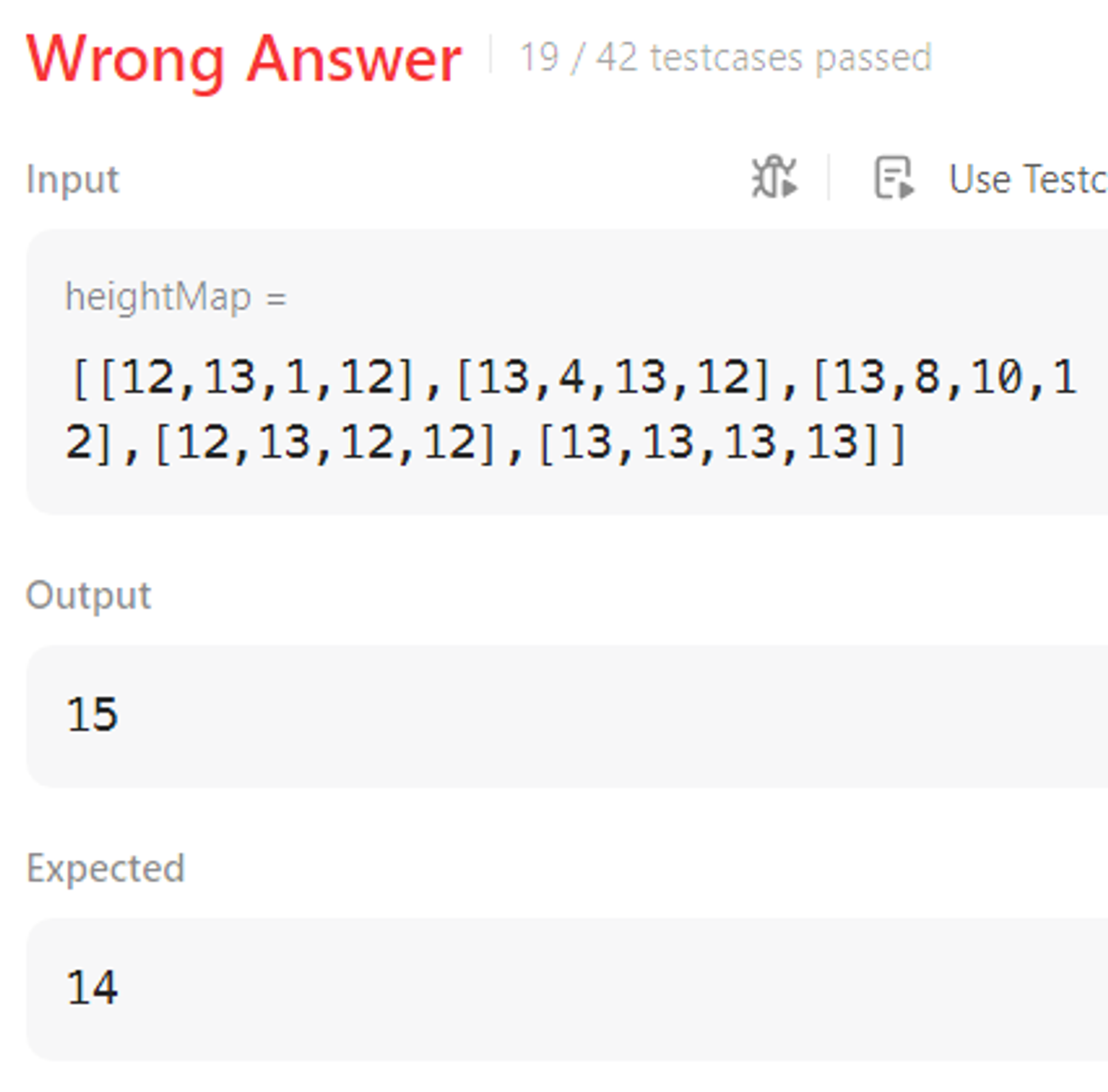
2차 시도(25분 소요)
스터디 때 해설코드의 풀이방법을 아이디어에 대해서만 들었고, 해당 아이디어를 활용해 구현을 시도했다.
아이디어의 핵심은 테두리부터 정의하면서 내부의 물을 채워주는 방식이다. 테두리를 기준으로 안쪽에 있는게 더 작으면 당연히 안쪽에 물이 차게 되니까, min_heap에 모든 테두리 index 를 넣어주고, 방문여부를 확인하여 상하좌우를 확인하고
만약 다음 노드가 더 높거나 같은 노드라면, 해당 노드를 힙에 푸시,
만약 다음 노드가 더 낮은 노드라면,
현재노드와 해당 노드의 차이만큼 물을 채워주고
물을 누적합으로 결과변수에 저장해주고
해당 노드를 힙에 넣어준다.
import heapq
class Solution:
def trapRainWater(self, heightMap: List[List[int]]) -> int:
dr = [0,1,0,-1]
dc = [1,0,-1,0]
min_heap = []
M = len(heightMap)
N = len(heightMap[0])
visited = [[False for _ in range(N)] for _ in range(M)]
for row in range(len(heightMap)):
for col in range(len(heightMap[0])):
if row == 0 or row == M-1:
heapq.heappush(min_heap,[heightMap[row][col],row,col])
visited[row][col] = True
if col == 0 or col == N-1:
if row != 0 and row != M-1:
heapq.heappush(min_heap,[heightMap[row][col],row,col])
visited[row][col] = True
result_water = 0
while min_heap:
th,tr,tc = heapq.heappop(min_heap)
for i in range(4):
nr = tr + dr[i]
nc = tc + dc[i]
if 0 <= nr < M and 0 <= nc < N and visited[nr][nc] == False:
if heightMap[nr][nc] >= th:
visited[nr][nc] = True
heapq.heappush(min_heap,[heightMap[nr][nc],nr,nc])
else:
visited[nr][nc] = True
result_water += th - heightMap[nr][nc]
heightMap[nr][nc] = th
heapq.heappush(min_heap,[heightMap[nr][nc],nr,nc])
return result_water배우게 된 점 [필수 작성]
반대로 생각하기
스터디 1번 문제나 스터디 2번 문제나 문제 접근이 어려울때는 아예 접근하는 방식을 정반대로 생각해보는게 해결책이 될 수 있다. 예를들어 1번 문제의 경우, 각 노드가 퍼져나갈 수 있는 최댓값을 저장하는게 아닌, 각 노드에 도달할 수 있는 최솟값을 저장한다거나, 2번 문제의 경우, 안쪽에서부터 채워나가는게 아닌, 바깥쪽에서부터 테두리를 정의하면서 들어온다거나 하는 것처럼 말이다.
질문 [ 필수 X ]
Q1
스터디 두문제 모두 첫단추부터 잘못 꿰메어 아이디어 로직 자체가 잘못되서 실제 코테였다면, 결과적으로 투자한 시간이 모두 의미가 없는 시간이 되버렸습니다. 초기 로직 자체가 잘못됐기때문에 디버깅조차 의미가 없게되버려 실제 코테라면 굉장히 치명적일 것 같은데, 어떻게 예방할 수 있을까요? 꼼꼼하게 더 코너케이스에 대해서 생각해보고 시작하는 수 밖에 없겠죠..?
A1
잘못된 접근방법은 누구나 빠질 수 있는 함정이다. 심지어 해당 문제의 경우 오히려 trapping rain water 1 을 풀었기 때문에 오히려 함정에 걸려들 확률이 더 높아지게된다. 실제로 교현님과, 코치님도 첫풀이방식때 나와 같은 접근방식을 택했다고 한다. 하지만, 중요한 점은 잘못된 접근방법으로 접근을 시작했더라도, 문제를 많이 풀어보면서, 잘못됐다는 것을 깨달은 순간 해당 문제를 커버할 수 있는 다른 접근방법을 빠르게 떠올릴 수 있는 능력을 기르는 것이 중요하다고 할 수 있다.
