다익스트라 알고리즘(Dijkstra Algorithm)

다익스트라 알고리즘 : DP를 활용한 최단 경로 탐색 알고리즘

• 하나의 정점에서 다른 모든 정점으로 가는 최단 경로를 알려줌. 단, 음의 간선은 포함x
• 현실에서는 음의 간선이 존재하지 않기 때문에 다익스트라는 현실 세계에 사용하기 매우 적합하다.
• "최단 거리는 여러 개의 최단 거리로 이루어져 있다." --> 다익스트라 알고리즘이 DP인 이유. 작은 문제는 큰 문제의 부분 집합에 속해 있다.
• 특징 : 하나의 최단 거리를 구할 때, 그 이전까지 구했던 최단 거리 정보를 그대로 사용한다.
• 활용 : 인공위성, gps 소프트웨어 등에서 가장 많이 사용되는 알고리즘

다익스트라 알고리즘 step by step

1. 출발 노드를 설정한다
2. 출발 노드를 기준으로 각 노드의 최소 비용을 저장한다.
3. 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택한다.
4. 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신한다.
5. 위 과정을 반복한다.

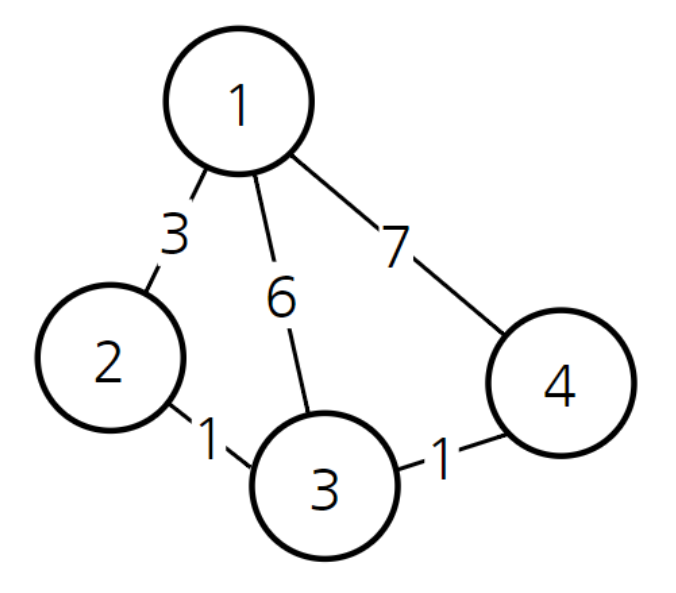
1. 1에 붙어 있는 2, 3, 4 확인했을 때 최단거리는 각각 3, 6, 7이므로 이 셋 기록.
   

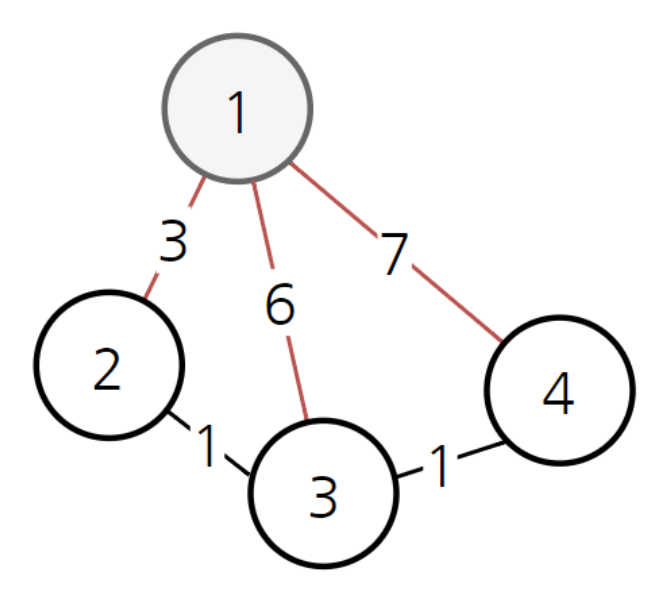
2. 가장 짧은 2로 감.
   나중에 컴퓨터는 1->2->3(비용 4)이 1->3(비용 6)보다 저렴하다는 걸 알게 됨. 더 저렴한 비용으로 갱신함. 이 과정 전까지는 1->3으로 가는 최소 비용이 6인줄 알았는데 더 짧은 거리 발견했으니 4로 갱신.
   

---

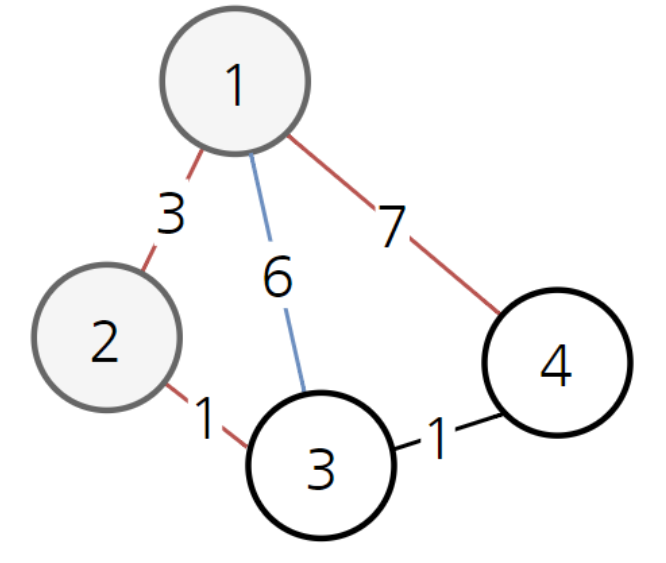
• 다익스트라 알고리즘은 이차원 배열로 처리해야 한다.
  

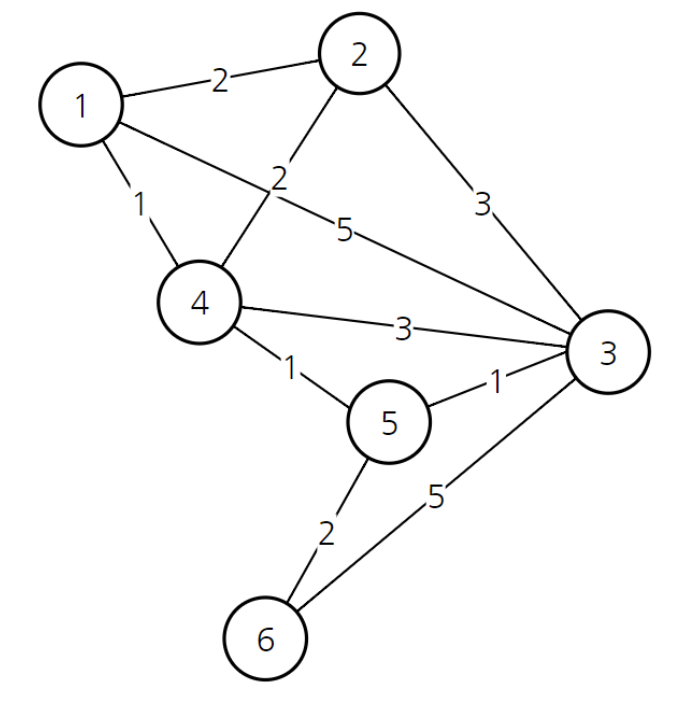
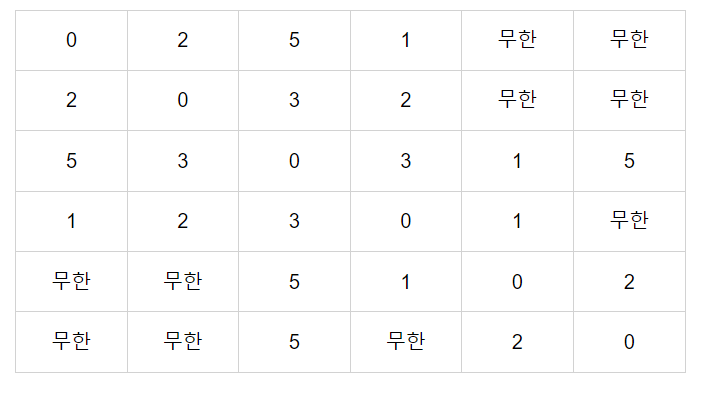
아래 표는 위 그래프를 이차원 배열로 나타낸 것이다. 특정 행에서 열로 가는 비용이다.
1행 3열의 값이 5 => 1번 노드에서 3번 노드로 가는 비용이 5라는 것.

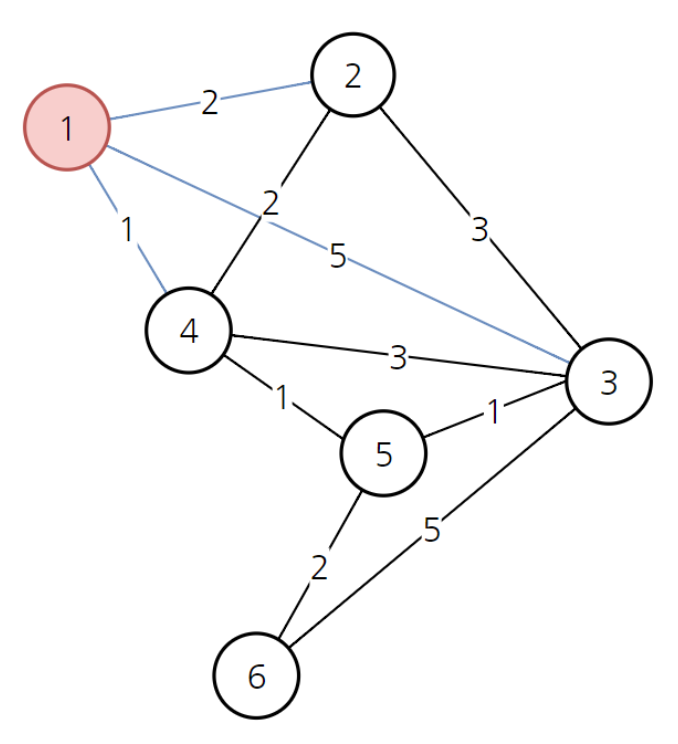
1. 1번 노드 선택. 1번 노드와 이어진 노드는 2, 3, 4다. 비용은 각각 2, 5, 1이다. 5번, 6번 노드는 아직 비용을 모르니까 '무한'이라고 적어둔다.
   다음으로 갈 노드는 비용이 가장 적은 4번 노드를 선택한다.
   
   

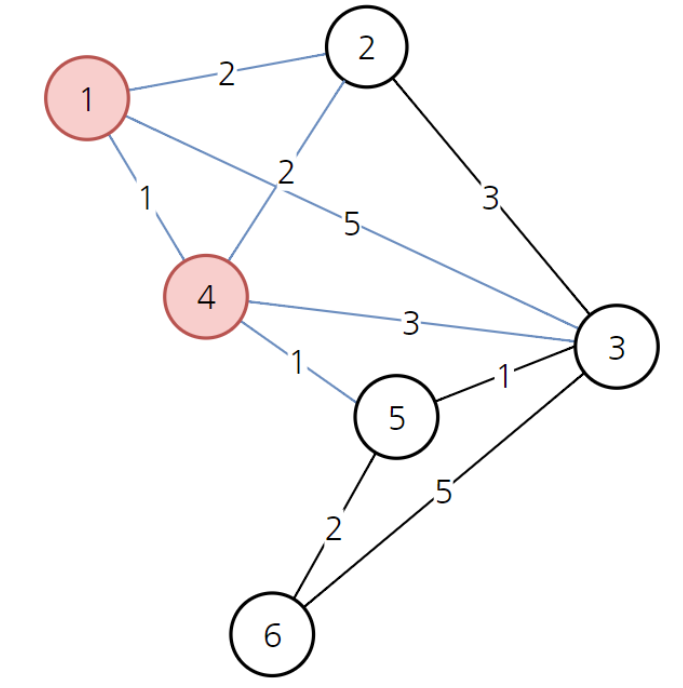
2. 4번노드는 2, 3, 5번 노드와 연결된다. 이제 3번 노드로 갈 수 있는 방법이 하나 생겼다. 1->3, 1->4->3. 근데 1->4->3 비용은 4로, 1->3의 비용(5)보다 적다. 따라서 3번 노드로 가는 비용을 4로 갱신해준다.
   또, 이제는 5로 갈 수 있는 길이 생겼으므로 5로 가는 비용도 2로 갱신해준다.
   
   

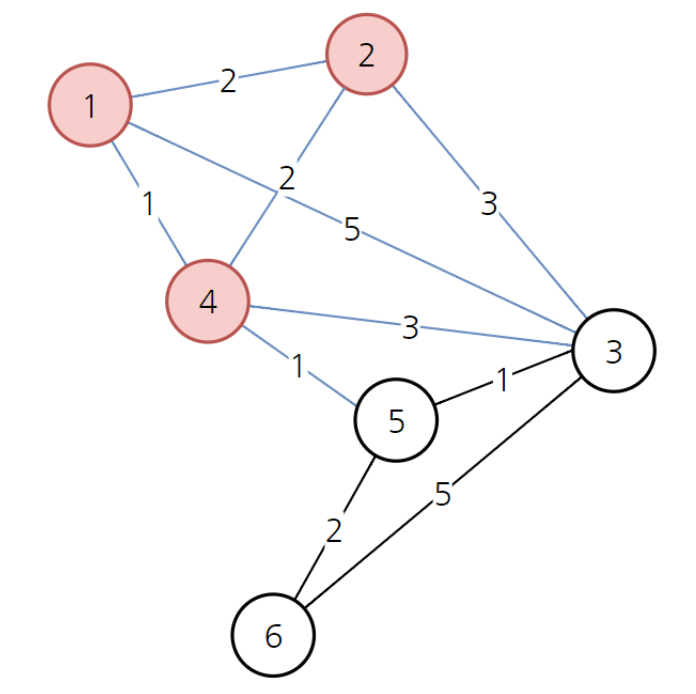
3. 이제 아직 방문하지 않은 노드 중 가장 비용이 적은 노드인 2번 노드로 간다. 경유해서 2번 노드로 가더라도(1, 4, 3번 노드) 비용(2, 3, 7)이 갱신되는 경우는 없다.
   
   

4. 방문하지 않은 노드 중에서 비용이 가장 적은 5번 노드로 간다. 1->4->5->3(비용 3) 이 1->5(비용 5)보다 저렴하다. 따라서 노드 3으로 가는 비용을 3으로 갱신한다.
   1->4->5->6(비용 4)도 기존의 무한보다 저렴하므로 갱신한다.

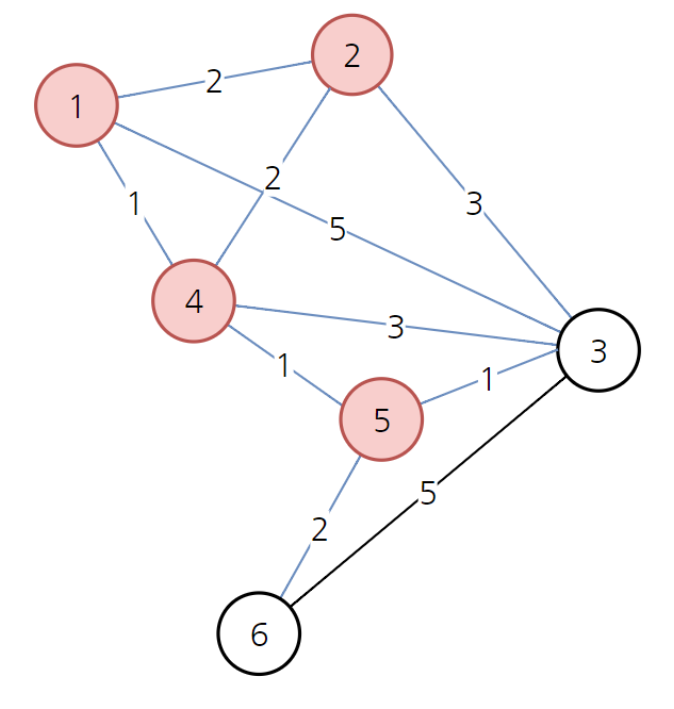
5. 방문하지 않은 노드 중에서 가장 저렴한 노드 3번으로 간다. 3이랑 이어진 노드는 2, 4, 5, 6인데 각각 모두 3을 거쳐가는 것보다 이미 가지고 있는 값이 더 작기 때문에 갱신할 필요가 없다.

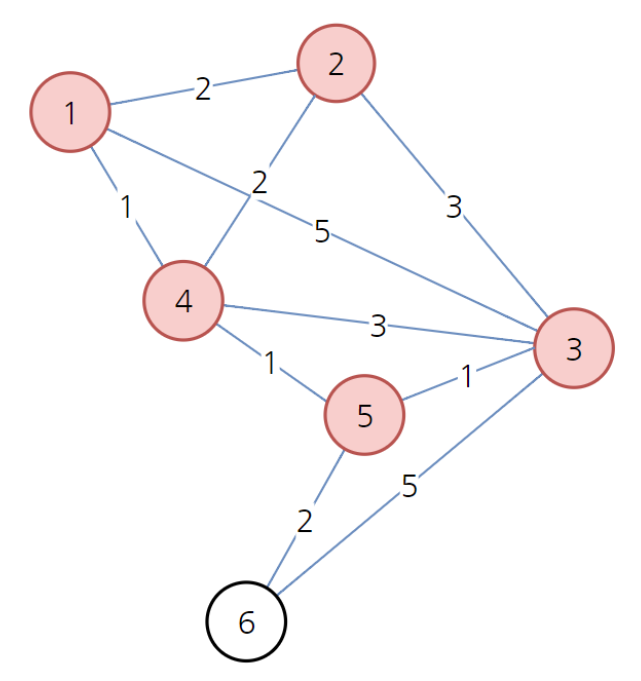
6. 마지막으로 남은 노드 6번으로 간다. 6번 노드랑 이어진 노드 5, 3도 6번을 거쳐가면 최솟값을 얻을 수 없다. 따라서 갱신할 필요가 없다.
   

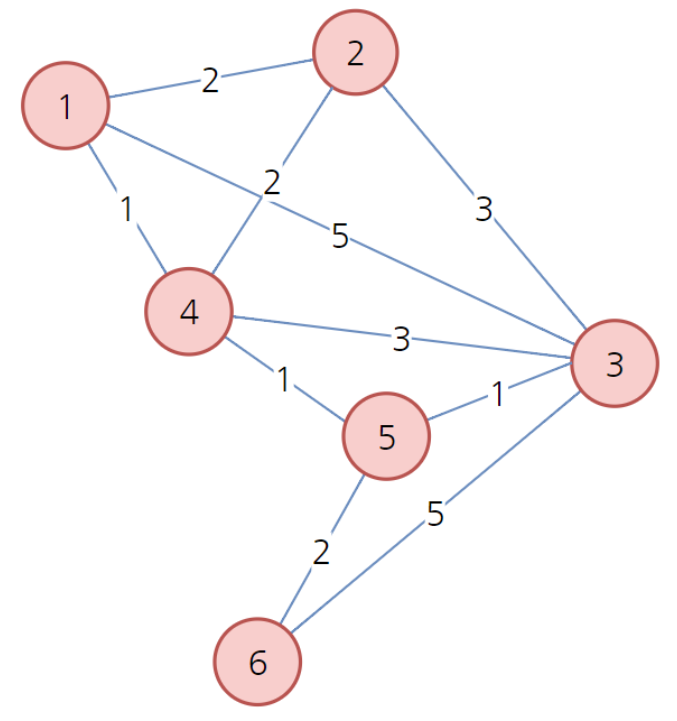
따라서 최종 배열은 다음과 같다.

---

자바스크립트 코드

1. 그래프를 인접리스트로 표현한다. 그래프는 정점과 간선으로 이루어져 있고, 각 간선은 두 정점과 그 사이의 가중치를 갖는다.
2. 다익스트라 알고리즘으 구현한다.

const graph = {
  A: { B: 5, D: 9, E: 2 },
  B: { A: 5, C: 2 },
  C: { B: 2, D: 3 },
  D: { A: 9, C: 3, F: 2 },
  E: { A: 2, F: 3 },
  F: { D: 2, E: 3 },
};


function dijkstra(graph, start) {
  const distances = {};
  const visited = new Set();
  const priorityQueue = new MinPriorityQueue();

  // 그래프 초기화 : 각 정점의 거리를 무한대로 설정하고 시작 정점의 거리는 0으로 설정합니다.
  for (const vertex in graph) {
    distances[vertex] = Infinity;
  }
  distances[start] = 0;

  // 우선순위 큐 사용: 최소 우선순위 큐를 사용하여 현재 최단 거리의 정점을 선택합니다.
  priorityQueue.enqueue(start, 0);

  while (!priorityQueue.isEmpty()) {
    const { element: currentVertex } = priorityQueue.dequeue();
    visited.add(currentVertex);
// 인접 정점 탐색: 현재 정점의 인접 정점을 탐색하며 거리를 갱신합니다.
    for (const neighbor in graph[currentVertex]) {
      if (!visited.has(neighbor)) {
        const newDist = distances[currentVertex] + graph[currentVertex][neighbor];

        if (newDist < distances[neighbor]) {
          distances[neighbor] = newDist;
          priorityQueue.enqueue(neighbor, newDist);
        }
      }
    }
  }
// 결과 반환: 모든 정점에 대한 최단 거리를 반환합니다.
  return distances;
}

// MinPriorityQueue 클래스 구현
class MinPriorityQueue {
  constructor() {
    this.queue = [];
  }

  enqueue(element, priority) {
    this.queue.push({ element, priority });
    this.queue.sort((a, b) => a.priority - b.priority);
  }

  dequeue() {
    return this.queue.shift();
  }

  isEmpty() {
    return this.queue.length === 0;
  }
}

// 테스트
const startVertex = 'A';
const distances = dijkstra(graph, startVertex);
console.log(distances);

공통문제 : https://www.acmicpc.net/problem/1446
문제과제추천 : https://www.acmicpc.net/problem/18352

참고 : https://han-joon-hyeok.github.io/posts/dijkstra-algorithm/
https://m.blog.naver.com/ndb796/221234424646