Erneset Ryu 교수님의 2022학년도 2학기 <심층신경망의 수학적 기초> 과목을 듣고 필자가 요약해 정리한 글입니다.

Introduction

Variational Autoencoder에 대해 설명하기 전에, 그 전단계인 Autoencoder에 대해 알아보고 넘어가자.
Autoencoder는 이미지처럼 높은 차원의 입력 데이터를 잠재 공간(latent space)상의 저차원의 표현 벡터로 압축하는 인코더와, 다시 잠재 공간의 벡터를 원본으로 복원하는 것을 목표로 하는 디코더로 구성된 신경망이다. 인코더의 입력과 디코더의 출력의 차이(예를 들어 MSE)를 손실 함수로 설정함으로써, 인코더는 원본 이미지의 특성을 잘 살려서 벡터로 표현하는 방법을 학습하게 되고, 디코더는 표현 벡터만을 보고 원본 이미지에 가깝게 복원하는 방법을 학습하게 된다.

여기서 디코더가 표현 벡터만을 보고 원래의 이미지를 복원해낸다는 점에 주목하자. 즉, 표현 벡터에는 원래 이미지의 중요한 정보들이 다 담겨있다는 것이다. 즉, 표현벡터는 원본 이미지에 담긴 특성(feature)들을 뽑아 저장해놓은 차원 축소의 역할을 한다고도 볼 수 있을 것이다. 실제로 VAE를 데이터의 차원을 축소하는 데 사용하는 경우가 많다.

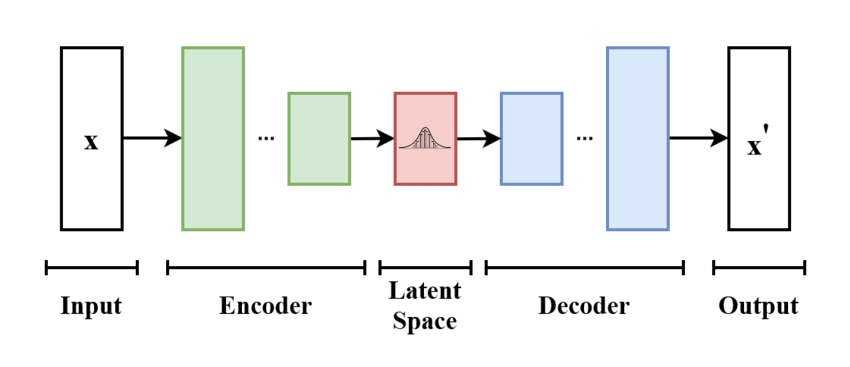
Variational Autoencoder는 Autoencoder에 확률적인 개념을 더해 개선한 것이다. 이 글에서는 VAE가 왜 타당한 모델인지, 그 motivation은 어디에서 나왔는지를 수학적으로 설명한 부분들을 정리해보려고 한다.

Key Idea of VAE

Variational Autoencoder는 크게 latent vector $z$가 주어졌을 때, 이미지의 확률분포를 나타내는 인코더 $p_\theta(x|z)$와, 이미지 $x$가 주어졌을 때 latent vector $z$의 분포를 설명하는 디코더 $q_\phi(z|x)$의 두 부분으로 구성된다. Autoencoder를 이해했다면 왜 저 두 함수가 각각 인코더와 디코더로 불리는지 쉽게 이해할 수 있겠지만 우선은 '인코더, 디코더'라는 명칭에 대해서는 넘어가기로 하자. 여기에서는 왜 저 두 함수가 필요한지를 조금 다른 motivation을 사용해 설명할 것이다.

목표: Maximum Likelihood Estimation

먼저, $N$개의 이미지(예를 들어서 $N$장의 고양이 사진) $X_1, X_2, \cdots, X_N$가 주어져 있다고 생각하자. 우리의 목표는 이러한 고차원의 이미지들의 기저에 있는, underlying structure를 이해하는 것이다. 다르게 말하자면, $N$장의 고양이 사진들은 "고양이 사진의 확률분포"에서 $N$번 샘플링된 것이라고 가정할 수 있으며, 그 확률밀도함수 $p_X(x)$를 알아내는 것을 목표로 삼을 수 있을 것이다.

이는 늘 그렇듯이 최우도추정(maximum likelihood estimation, MLE)을 통해서 할 수 있다. IID로 $p_X(x)$에서 샘플링을 했을 때, 저 $N$개의 이미지가 모두 나올 확률(정확히는 likelihood)은

가 되므로 이를 최대화하면 되는 것이다. 곱으로 이루어진 식은 다루기 어려우므로 로그를 씌우면 우리의 목표는

가 된다. $p$라는 함수가 $\theta$로 매개화되는 함수라고 하면, 다시

로 쓸 수 있을 것이다. 이때 $p_\theta$는 신경망으로 구현되며, $\theta$는 그 가중치가 될 것이다.

그런데 autoencoder에서 설명했듯이 이미지 $X$에는 그 기저에 $Z$라는, 이미지의 특성을 설명하는 변수가 있어 $Z$만 알면 $X$가 거의 결정된다고 할 수 있다. 따라서 전확률공식과 조건부확률을 사용해서

로 쓸 수 있다. 그러면 다시 우리의 목표는

로 바뀌게 된다. $p_Z$는 여기서 알려져있는 함수로, 일반적으로 (다변수) 표준정규분포를 사용한다.

Importance Sampling

이제 위의 식을 어떻게 최대화할지를 생각해봐야 할 것이다. 여기서 문제점은 식에 기댓값이 끼어있다는 것이다. $Z$가 이산확률변수라면 그냥
$\mathbb{E}_{Z \sim p_Z}[p_\theta(X|Z)]=\sum_i p_Z(z_i)p_\theta(X|z_i)$
처럼 다 더해버리면 된다. 하지만 $Z$는 연속적인 분포를 가지기 때문에 $\int p_\theta(X|z)p_Z(z) dz$를 계산해야 하며, 이는 굉장히 어렵다. 이 때문에 $Z_i$를 샘플링해서 $\mathbb{E}$의 근사값을 구해 사용하게 된다.

사실 위의 식은 각 이미지 $X_i$에 대해서, 그 이미지를 만들어낸(만들어냈을 것이라고 생각되는) latent vector $Z$를 한개씩만 샘플링하여 구하기 때문에 매우 부정확한 근사이다. 따라서 우리는 Importance Sampling이라는 개념을 도입해서 이를 해결한다.

Importance Sampling의 개념

$X$가 $f(x)$라는 확률밀도함수를 가질 때 $\mathbb{E}_{X\sim f}[\phi(X)]$를 구해야 하는 상황을 생각해보자. 그런데 적분을 실제로 해서 이를 구하는 것이 어려운 상황이 많기 때문에 위와 같이 많은 경우 $X$를 적당히 샘플링해서

과 같이 근사해서 사용한다. 이를 Monte Carlo Estimation이라고 한다. 큰 수의 법칙에 의해, $N$이 커지면 커질수록 우변은 실제 기대값과 매우 유사한 값을 가지게 될 것이다.

하지만 위와 같은 근사는 때때로 분산이 너무 커서 실제로는 사용하기 힘들거나, $N$이 아주 커야 정확해질 때가 많다. 따라서 Importance Sampling이라는 개념을 사용해서 분산을 줄이게 된다. Importance Sampling의 핵심은 X의 분포 함수 $f$를 다른 "좋은" 함수 $g$로 바꾸는 것이다. 이를 위해 아래와 같은 테크닉을 사용한다.

이는 기대값을 사용해 아래와 같이 쓸 수 있다.

앞서 말했듯이, $X$가 따르는 분포(확률밀도함수)가 $f$에서 $g$로 바뀐 것을 볼 수 있을 것이다. $g$를 적절하게 선택하면 원래보다 더 정확한(variance가 낮은) 추정을 할 수 있게 된다.

그러면 $g$는 어떻게 선택해야 할까? 이상적으로는

로 놓으면 분산이 0으로 최소가 된다. 그런데 $I$는 우리가 알고 있는 값이 아니므로($I = \mathbb{E}_{X\sim f}[\phi(X)]$이므로 $I$를 알고 있다면 애초에 이 짓을 할 필요가 없다) 이러한 함수는 우리가 사용할 수 없다.

따라서 $g$가 이상적인 함수 $\frac{\phi(X)f(X)}{I}$와 갖는 거리를 구해서, 이것이 최소화되도록 함으로써 어느 정도 좋은 $g$를 구할 수 있다. $g$는 $\theta$로 parametrize된 신경망으로 구성되어 있다고 가정하자. KL-Divergence를 사용하면,

이며, $\log I$는 $\theta$에 대해서는 상수이므로 $\mathbb{E}_{x\sim g_\theta}\left[{\log\left(\frac{g_\theta (X)}{\phi(X)f(X)}\right)}\right]$를 SGD를 사용해서 최소화하면 된다. 이렇게 구한 $g_\theta$를 사용하여 Importance Sampling을 하면 $I$를 비교적 낮은 variance로 추정할 수 있다.

$Z$를 importance sampling하자

이제 원래의 문제로 돌아와서, 이미지 $X_i$에 대해

를 $Z_i\sim q_i(z)$를 사용한 importance sampling을 통해 근사해 보자.

이때 $q_i$는 앞서 설명한 것과 마찬가지로

일 때 최대가 될 것이다. 그런데 베이즈 정리에 의해서, 이는 $p_\theta(z|X_i)$와 같다. 물론 이는 정확하게 계산이 불가능하며($p_\theta(X_i)$를 모르니), KL-Divergence 를 통해 $q_i^*$와 최대한 비슷한 $q_i$를 찾아야 한다.

마지막 줄에서, $\log p_\theta(X_i)$는 $Z$와 무관한 항이므로 최소화할 때 무시해줘도 된다. 그러면 $q_i(Z)$, $p_\theta(X_i|Z)$, $p_Z(Z)$는 모두 우리가 계산할 수 있는 항들이므로 $q_i$를 잘 조절함으로써 최소화가 가능하다.

Amortized Inference

그런데 위에서 $q_i$를 보면 index $i$가 붙어있는 것을 알 수 있다. 즉, 각 데이터(이미지) $X_i$에 대해서 개별적으로 최적화 문제를 풀고 있는 것이다. 당연히 이는 계산이 매우 많이 걸릴 것이다.

따라서 우리는 함수 $q$를 신경망으로 구성하고, 그 가중치 $\phi$로 parametrize하여 $q_\phi$로 만든다. 그리고

를 loss 함수로 삼아서 SGD를 사용해 최소화한다. 이렇게 하면, $q_\phi$는 넣어주는 이미지 $X_i$에 따라서 다른 분포 $q_i(z)$를 나타내게 된다. 즉 하나의 함수 $q_\phi(z|X)$만으로 $N$개의 계산과정을 대신할 수 있는 것이다. 즉,

가 되는 것이다. 이 $q_\phi$가 바로 인코더가 된다.

Encoder와 Decoder의 최적화

이제 인코더 $q_\phi$와 $p_\theta$를 최적화하면 된다. 먼저 인코더의 목표는 앞에서 설명한 것처럼 각 이미지 $X_i$에 대해 importance sampling을 하는 최적의 함수 $q_i^*$를 amortized inference로 근사하는 것이 된다.

디코더의 목표는 (당연히) Maximum Likelihood Estimation을 수행하는 것이다.

우연히도 두 식의 형태가 똑같은 것을 알 수 있다! 따라서 위 식을 최대화하는 $\theta$와 $\phi$를 찾으면 된다. 즉,

를 찾는 것이 VAE의 training objective가 된다.