
10진법과 2진법
8, 12, 20
10진법은 0~9를 이용하는 수 체계입니다.
우리 사람이 가장 많이 사용하는 수이죠.
00001000, 00001100, 00010100
2진법은 0과 1을 이용하는 수 체계입니다.
주로 컴퓨터를 다룰 때 사용합니다.
2진법과 비트
1개의 비트는 0과 1을 저장할 수 있다는 거 기억나시죠?
2진법은 다음과 같이 저장됩니다.
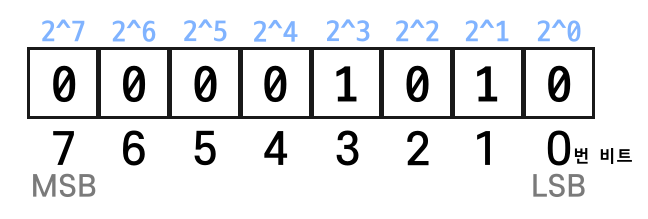
각 비트에 저장되어 있는 값을 모아보니 2진법 수인 00001010이 나옵니다.
이것은 10진법으로 10입니다.
어떻게 계산했는지 모르겠다고요?
계산하는 방법은 다음과 같습니다.
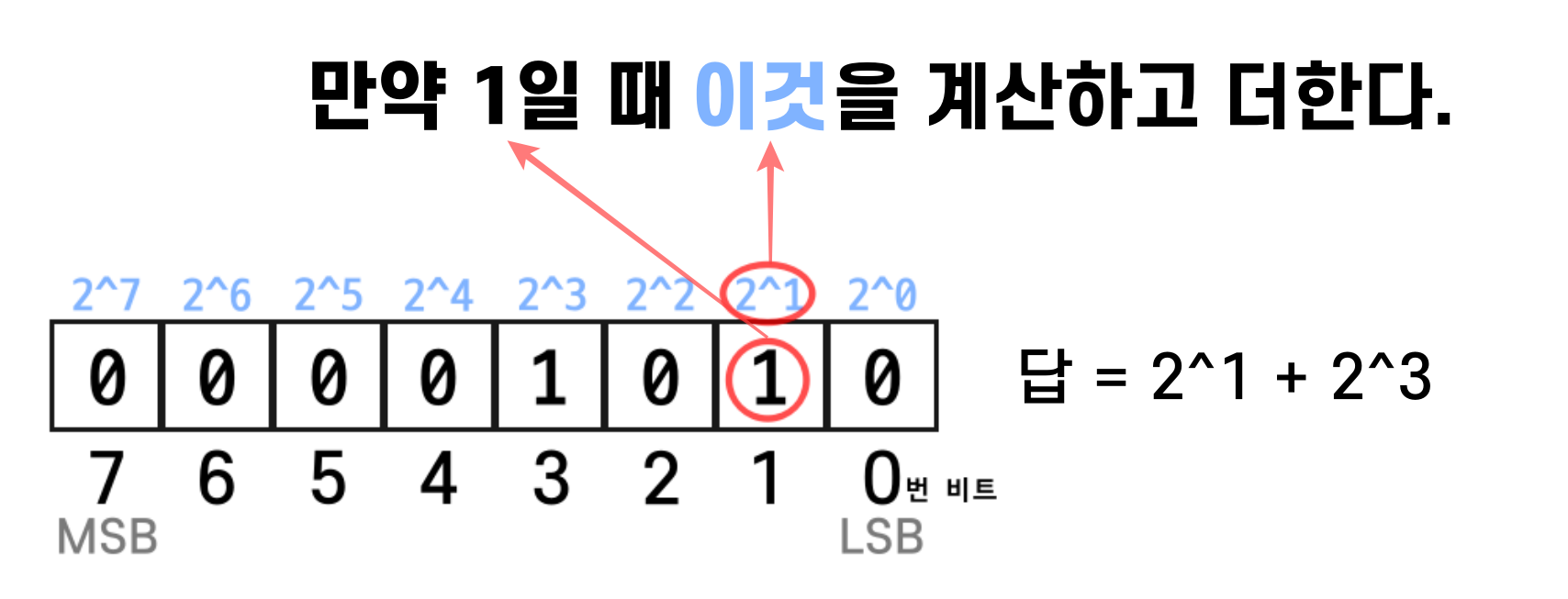
비트의 값이 1인 것을 모두 찾은 다음 2^(자리수) 하여 계산합니다.
2진수의 자리수가 올라갈 때마다 승수도 함께 올라가는 것을 볼 수 있습니다.
계산 과정을 보면 각 자릿수에 숫자 0과 1만 넣어져 있음을 볼 수 있습니다.
즉, 표현법이 2진법과 동일하며, 10진수로 변환하는 과정 또한 같음을 알 수 있습니다.
2진법의 장단점
컴퓨터를 다룰 때 2진법을 사용하는 이유는 위와 같이 0과 1. 즉 최소 단위가 ON/OFF이기 때문에 해당 메모리의 값을 빠르게 파악할 수 있기 때문입니다.
값이 1인 비트가 몇 개인지 파악하고자 할 때가 그 예가 되겠지요.
하지만 그만큼 숫자가 길어지는 게 단점입니다.
10진법과 2진법을 예로 들면..
1 = 00000001
위와 같이 자릿수를 많이 차지함을 알 수 있습니다.
그리고 보시다시피 2진법은 값을 한눈에 파악하기 힘든 수입니다.
(0010011001100101이라는 수의 값이 뭔지 바로 답할 수 있는 사람은 매우 적을 겁니다)
16진법
16진법은 숫자와 문자로 이루어진 수 체계이고, 0~9까지는 숫자를, 10~15부터는 문자(A~F)를 사용하여 수를 나타냅니다.
다른 수 체계와의 차이점을 비교해보자면 다음과 같습니다.
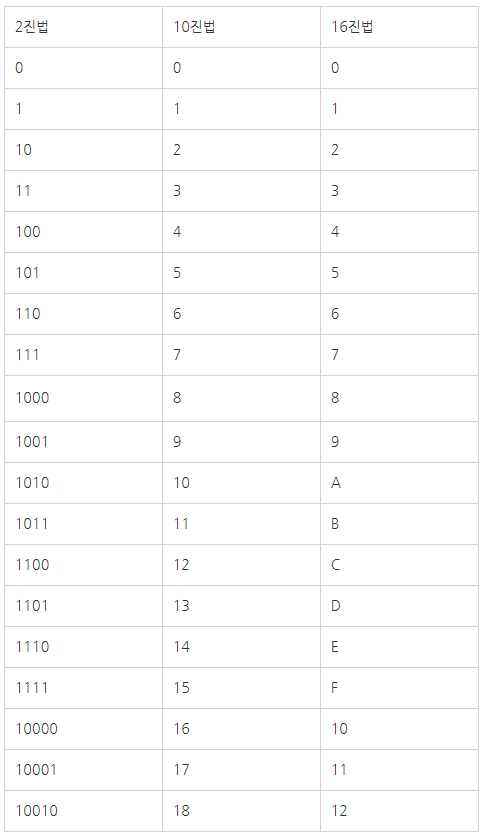
16진법의 특성에 대해 설명하겠습니다.

1번.
16진법은 16개의 숫자와 문자를 이용하므로 위와 같이 4비트 값을 한 번에 표현할 수 있습니다.
이는 16진법이 해당 값의 바이트 크기를 파악할 수 있다는 말도 됩니다.
예를 들어 16진수 1234AB는 4비트 값이 6개 있고, 저장하기 위해선 3바이트가 필요하다고 할 수 있습니다.
2번.
16진법은 10진수보다 더 짧게 적을 수 있습니다.

16진법은 문자의 존재로 인해 10진수보다 수가 더 작게 나오는데, (위의 사진엔 없지만) 만약 10진수가 그리 크지 않은 백의 자리 수라면 16진법은 십의 자리 숫자만으로 표현할 수 있습니다.
10진수 250이 16진수로 fa인 것처럼요.
3번.
위의 특성을 바탕으로 하면 수를 메모리에 저장할 때 더 쉽게 저장할 수 있습니다.
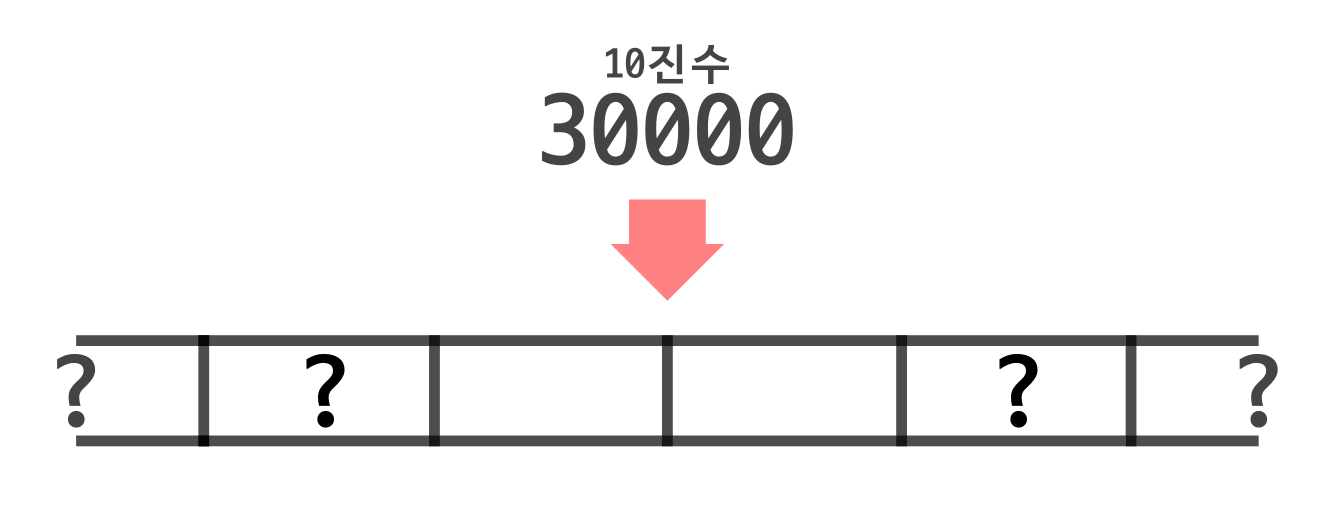
10진수인 30000을 메모리에 저장하려 합니다.
하지만 30000이란 수는 1바이트 메모리에 담을 수 없습니다. 1바이트 메모리가 지원하는 범위가 0~255이기 때문이죠.
따라서 2바이트에 걸쳐서 저장을 해야 하는데, 10진수로는 비트 단위로 작동되는 메모리에 바로 저장하기는 어렵습니다.
그렇다면 10진수를 4비트 값으로 변환해봅시다.
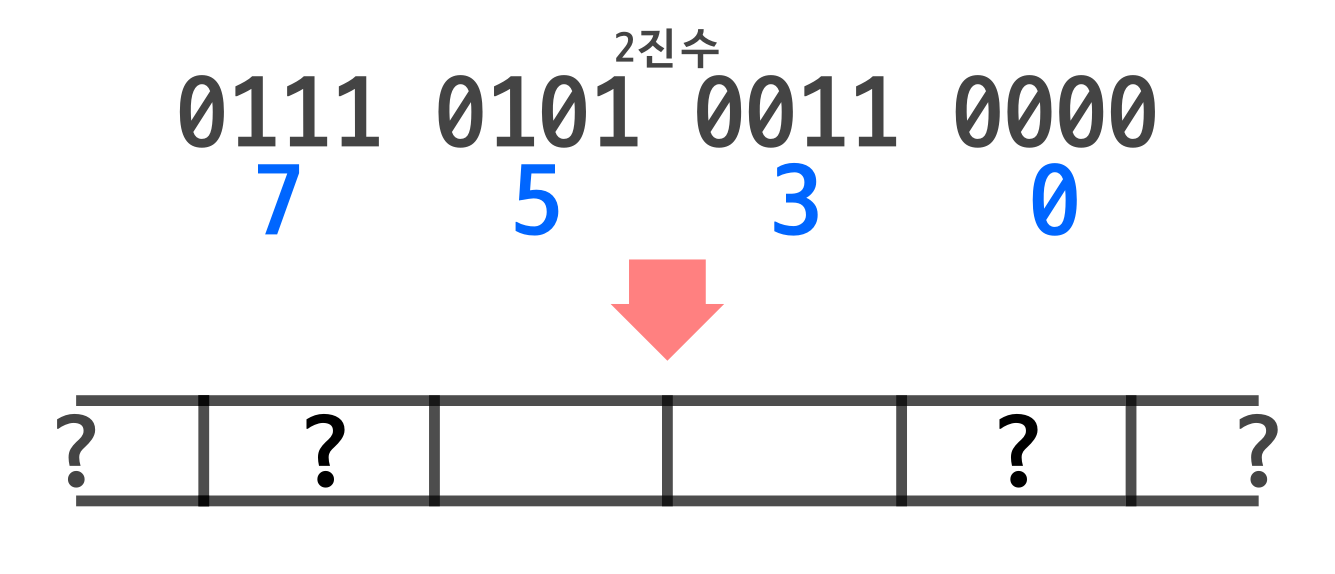
10진수 30000을 4비트 값으로 변환하면 0111 0101 0011 0000 입니다.
이것을 각각 16진수로 바꾸면
0111 = 7
0101 = 5
0011 = 3
0000 = 0 이므로

메모리에 75와 30으로 저장됨을 알 수 있습니다.
이때 저장되는 순서에 유의해야 합니다.
저장되는 방식은 빅 엔디언과 리틀 엔디언으로 나뉩니다.
빅 엔디언(Big Endian)은 낮은 주소에 데이터의 높은 바이트(MSB)부터 저장하는 방식이고,
리틀 엔디언(Little Endian)은 낮은 주소에 데이터의 낮은 바이트(LSB)부터 저장하는 방식입니다.
간단히 그림으로 설명하자면

빅 엔디언의 경우는 75 30 순으로 저장되고,

리틀 엔디언의 경우는 30 75 순으로 저장됩니다.
