회귀분석으로 연속적 타깃 변수 예측
이번 장은
- 선형 회귀
- 주택 데이터셋 탐색
- 최소 제곱 선형 회귀 모델 구현
- RANSAC을 사용하여 안정된 회귀 모델 훈련
- 선형 회귀 모델의 성능 평가
- 회귀에 규제 적용
- 선형 회귀 모델을 다항 회귀로 변환
- 랜덤 포레스트를 사용하여 비선형 관계 다루기
로 이루어 져 있다.
이전 장은 지도학습 이면의 개념을 배웠다면 (그룹 소속이나 범주형 변수 예측하는 분류작업 위해 여러 모델 훈련) 이번 장에서는 지도 학습의 다른 카테고리인 회귀분석을 다룬다.
이번 장을 통해서 회귀모델의 주요 개념과 데이터 탐색 시각화, 선형 회귀 모델 구현하는 방법, 이상치에 민감하지 않은 회귀 모델 훈련, 회귀모델평가하고 문제점 분석, 비선형 데이터에 히ㅗ귀 모델 학습을 배운다.
(짱 중요해보이죠...)
선형 회귀
선형 회귀 목적 : 하나 이상의 특성과 연속적인 타깃 변수 사이의 관계 모델링
분류 알고리즘과 달리 레이블이 아니라 연속적인 출력값을 예측한다.
단순 선형 회귀
: 하나의 특성과 연속적인 타깃 사이의 관계 모델링 , 즉 x와 y 사이의 관계 모델링.
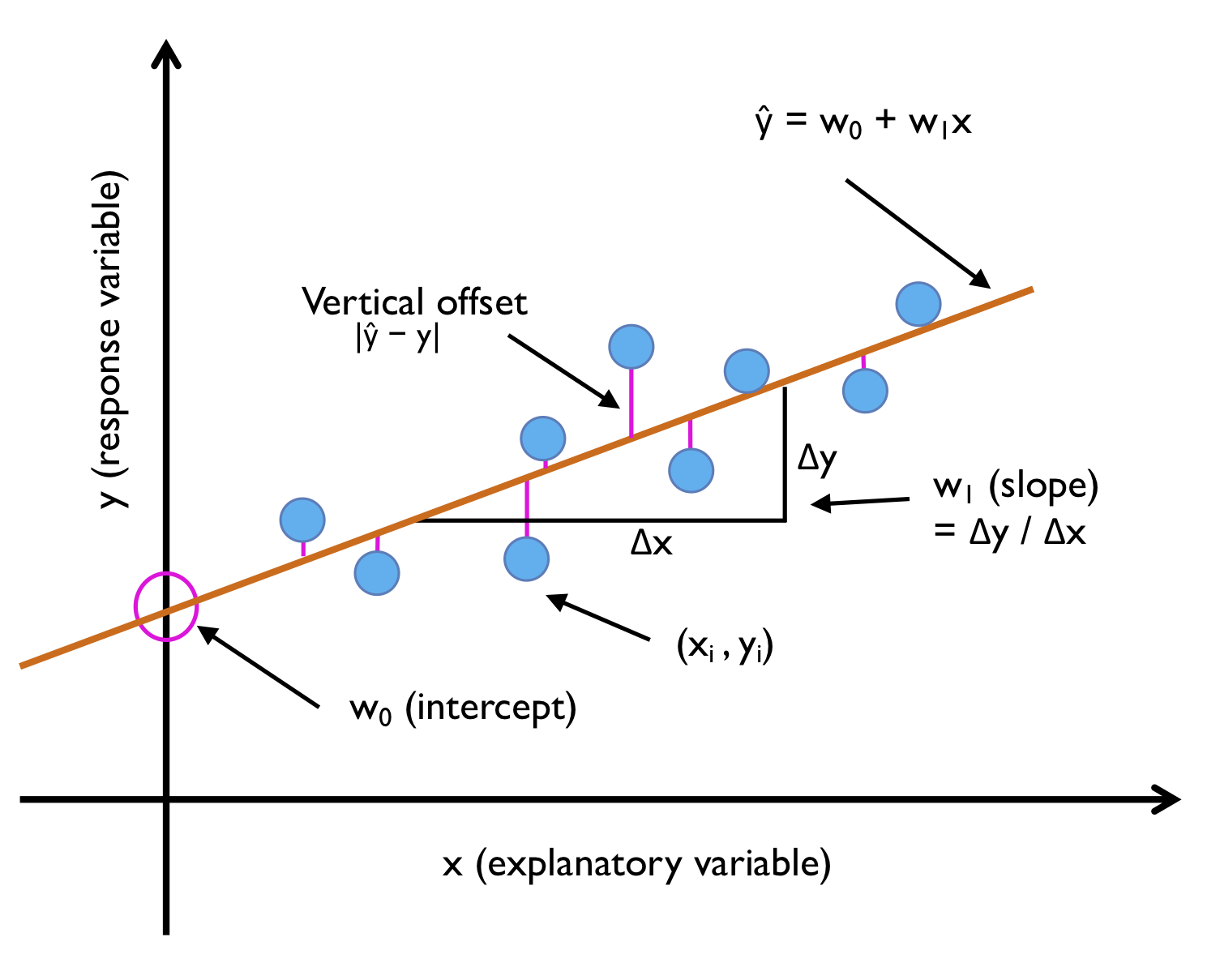
그러니까, 샘플 포인트를 가장 잘 맞춰서 통과하는 직선!
데이터에 가장 잘 맞는 직선을 회귀 직선 (regression line)이라고도 한다. 회귀 직선과 훈련 샘플 사이의 직선 거리를 오프셋 (offset) 또는 예측 오차인 잔차 (resident)라고 한다.
짚고 넘어갈거
- 특성 = 설명변수 = x = explanatory variable
- 타깃 = 응답변수 = 반응변수 = y = response variable
다중 선형 회귀
특성이 하나면 단순 선형, 여러 개면 다중 선형 회귀이다.
선형 회귀 모형은 여러 개의 특성이 있는 경우로 일반화 가능
특성 두개인 다변량 회귀 모델이 학습한 2차원 초평면 예시
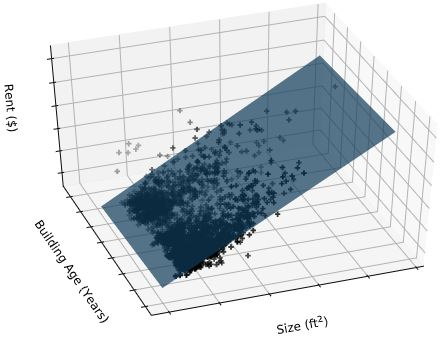
책에서는 단변량 회귀사용해 하나의 특성 가진 예제와 그래프 주로 다룰 예정 (복잡하니까, 단변량 회귀와 다변량 회귀는 같은 개념과 평가기법 사용함)
주택 데이터셋 탐색
1978년 수집된 보스턴 교외 지역의 주택 정보 가지고 있음
데이터는 여기서 확인가능
https://github.com/rickiepark/python-machine-learning-book-3rd-edition/blob/master/ch10/housing.data.txt
import pandas as pd
df = pd.read_csv('https://raw.githubusercontent.com/rasbt/'
'python-machine-learning-book-3rd-edition/'
'master/ch10/housing.data.txt',
header=None,
sep='\s+')
df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS',
'NOX', 'RM', 'AGE', 'DIS', 'RAD',
'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
df.head()head 보면 13개의 특성이 나옴. CRIM- 도시의 인당 범죄율
ZN - 2만 5천평방 피트가 넘는 주택 비율, INDUS - 도시에서 소매 업종이 아닌 지역 비율, MEDV- 자가 주택의 중간가격(1천달러 단위) 등의 특성 을 가진다.
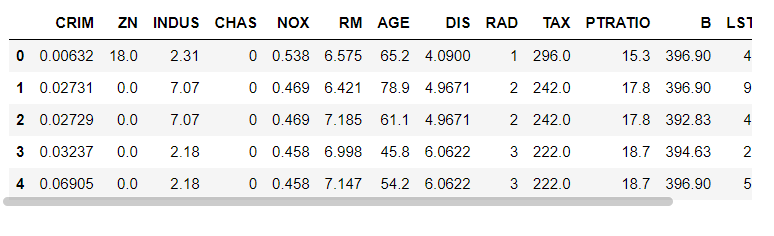
이 장 나머지 부분 MEDV 을 타깃으로 삼는다.
탐색적 데이터분석 (EDA)은 머신러닝 모델 훈련 전에 권장되는 단계로 EDA 그래픽 도구 중 산점도 행렬 그려서 데이터셋의 특성간 상관관계 한번 시각화
pip install --upgrade mlxtend 로 mlxtend를 설치
import matplotlib.pyplot as plt
from mlxtend.plotting import scatterplotmatrix
cols = ['LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']
scatterplotmatrix(df[cols].values, figsize=(10, 8),
names=cols, alpha=0.5)
plt.tight_layout()
# plt.savefig('images/10_03.png', dpi=300)
plt.show()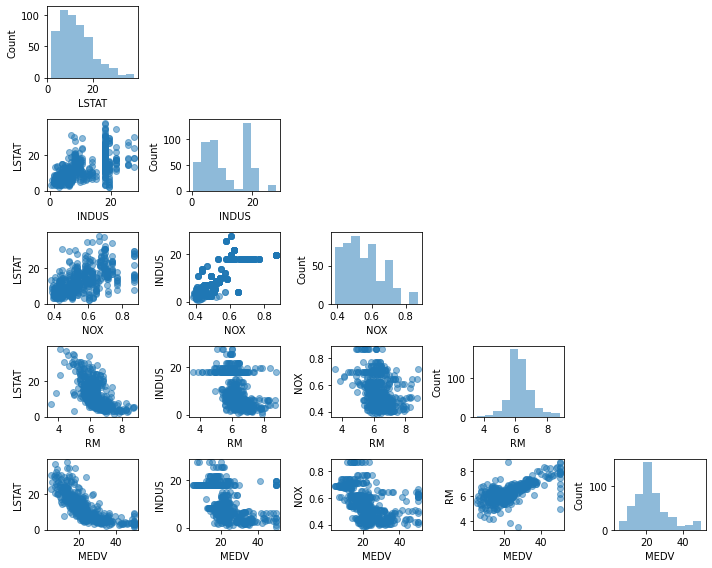
산점도 행렬 시각적 요약 잘된다.
짚고 넘어갈 것
- 데이터셋의 특성 간 관계를 파악하는게 중요
- 산점도 행렬 통해 데이터 분포 형태, 이상치 포함하고 있는지 확인 가능
- 선형 회귀 모델을 훈련할 때 타깃이 정규분포를 따를 필요 없다. (특정 통계와 가설 검정에 정규분포가 필요하기 때문이라고만 소개하고 있는데, 몰랐던 사실이니 기억해두자)
상관관계 행렬 사용한 분석
상관관계 행렬 로 변수 간 선형 관계 정량화 하고 요약
( 특성이 표준화 되어있으면 상관관계 행렬과 공분산 행렬이 같다. )
상관관계 행렬은 피어슨 상관계수 (r) 를 포함한 정방행렬이다.
import numpy as np
from mlxtend.plotting import heatmap
cm = np.corrcoef(df[cols].values.T)
hm = heatmap(cm, row_names=cols, column_names=cols)
# plt.savefig('images/10_04.png', dpi=300)
plt.show()를 통해서 상관관계 행렬 히트맵 확인가능.
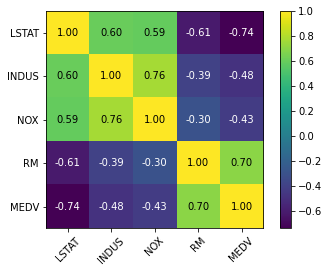
선형 회귀 모델 훈련하려면 타깃 변수 MEDV와 상관관계가 높은 특성이 좋다. 위의 히트맵을 보면 MEDV와 LSTAT 상관관계가 높다 (-0.74) 그리고 RM과 MEDV 사이의 상관관계도 0.7로 높다.
이제 앞의 산점도 행렬과 같이보면
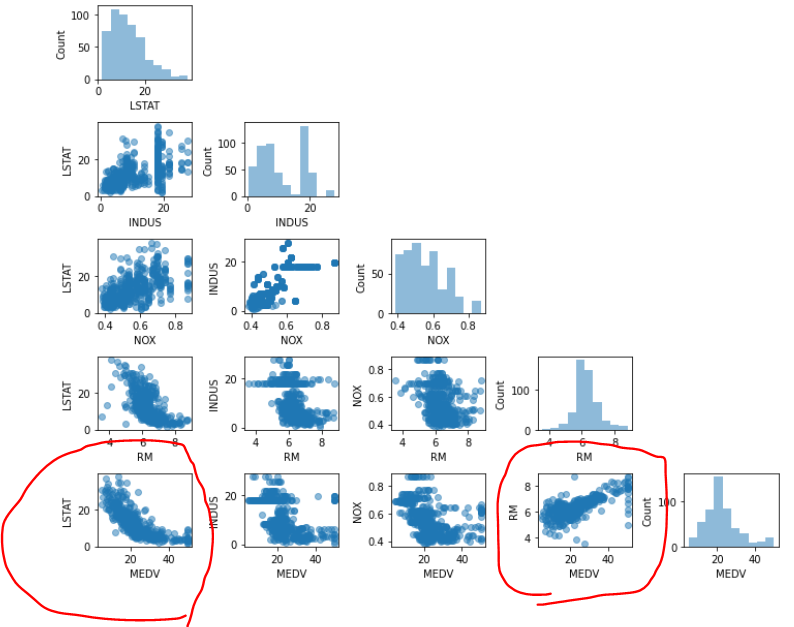
LSTAT 와 MEDV 간의 관계보다 RM과 MEDV 간의 관계가 선형성이 더 높아보이기 때문에 다음 절에서는 RM 사용.
짚고 넘어갈 것
- 산점도 행렬을 보고 끝이 아니라 상관관계 행렬 히트맵을 보고 함께 보면서 변수를 선택할 것
최소 제곱 선형 회귀 모델 구현
훈련 데이터의 훈련 샘플에 가장 잘 맞는 직선인 선형 회귀를 구하기 위해서는 최소 제곱법을 사용.
- 최소 제곱법 : 훈련 샘플까지의 수직 거리 (잔차 , 오차)의 제곱합을 최소화하는 선형 회귀 직선의 모델 파라미터 추정하는 방법
class LinearRegressionGD(object):
def __init__(self, eta=0.001, n_iter=20):
self.eta = eta
self.n_iter = n_iter
def fit(self, X, y):
self.w_ = np.zeros(1 + X.shape[1])
self.cost_ = []
for i in range(self.n_iter):
output = self.net_input(X)
errors = (y - output)
self.w_[1:] += self.eta * X.T.dot(errors)
self.w_[0] += self.eta * errors.sum()
cost = (errors**2).sum() / 2.0
self.cost_.append(cost)
return self
def net_input(self, X):
return np.dot(X, self.w_[1:]) + self.w_[0]
def predict(self, X):
return self.net_input(X)
class LinearRegressionGD : 2장에서 사용한 아달린의 경사 하강법 코드에서 단위 계단 함수 제거해 구현한 첫 선형 회귀 모델
RM 변수 특성으로 사용해 MEDV 예측하는 모델 훈련 + 특성 표준화 전처리
X = df[['RM']].values
y = df['MEDV'].values
from sklearn.preprocessing import StandardScaler
sc_x = StandardScaler()
sc_y = StandardScaler()
X_std = sc_x.fit_transform(X)
y_std = sc_y.fit_transform(y[:, np.newaxis]).flatten()
lr = LinearRegressionGD()
lr.fit(X_std, y_std)짚고 넘어갈거
-
특성 표준화 전처리.
-> y[:, np.newaxis]) : 사이킷런 대부분 변환기는 데이터가 2차원 배열 저장 기대해서 배열에 새로운 차원 추가하는 것.
--> 스케일 조정된 결과를 StandardScaler가 반환하면 flatten()를 통해 원래 1차원 배열 형태로 되돌리기! -
경사하강법 같은 최적화 알고리즘 -> 훈련 데이터셋 반복하는 에포크(전체 반복) 함수로 비용을 그래프로 그리면 좋다
비용 그래프
plt.plot(range(1, lr.n_iter+1), lr.cost_)
plt.ylabel('SSE')
plt.xlabel('Epoch')
plt.tight_layout()
# plt.savefig('images/10_05.png', dpi=300)
plt.show()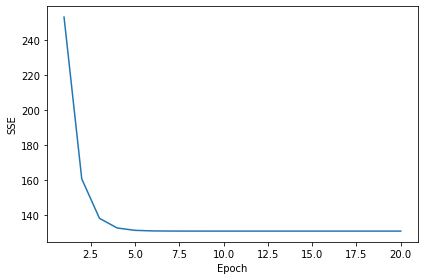
그래프 보면 다섯번째 애포크에서 수렴했다.
선형 회귀 모델이 <훈련데이터에 얼마나 잘 맞는지> 보기위해서 함수 만들어서 그래프를 그려보자
def lin_regplot(X, y, model):
plt.scatter(X, y, c='steelblue', edgecolor='white', s=70)
plt.plot(X, model.predict(X), color='black', lw=2)
return
lin_regplot(X_std, y_std, lr)
plt.xlabel('Average number of rooms [RM] (standardized)')
plt.ylabel('Price in $1000s [MEDV] (standardized)')
# plt.savefig('images/10_06.png', dpi=300)
plt.show()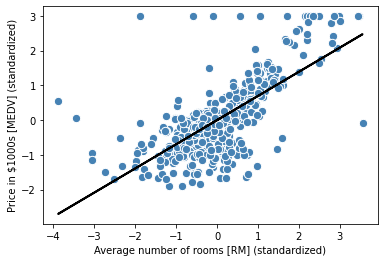
(과연 이 plot 에 나온것처럼 선형회귀가 데이터를 잘 설명하고 있나? ) 라는 의문이 든다면 정답이고
데이터 방개수가 주택 가격 잘 설명 못하는 경우도 많음을 설명한다.
y=3인 지점에서 여러 데이터 포인트 늘어서있는데, 저 부분 초과하는 가격 잘라냈다는 것 의미한다.
예측된 출력값을 원본 스케일로 복원해 제공해야하는데 예측가격을 원래 스케일인 1천달러 단위로 되돌리려면 inverse_transform 메소드 쓰면된다.
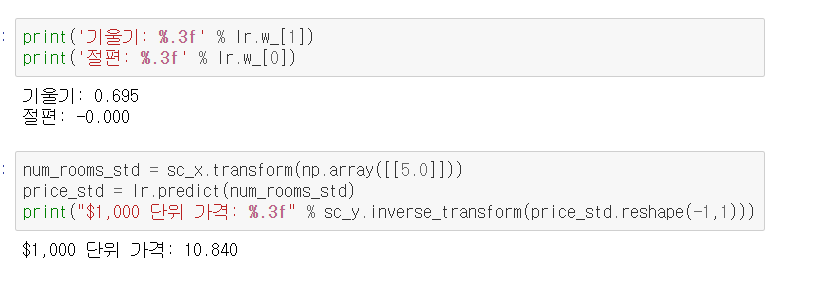
표준화 처리된 변수 사용할 때 기술적으로 절편 업데이트 필요없다. y 축 절편이 항상 0이기 때문이다.
근데 모델구현 이 방법이 최선일까
아니 당연히 사이킷런으로 추정 가능
사이킷런으로 회귀 모델의 가중치 추정
SciPy의 최소 제곱 구현 (scipy.linalg.lstsq)를 사용하는 사이킷런 추정기 사용.
사이킷런 선형 회귀 구현은 심지어 표준화되지 않은 특성에도 더 잘 동작한다!
경사 하강법 기반의 최적화 사용하지 않기 때문에 표준화 전처리 단계 건너뛰기 가능
from sklearn.linear_model import LinearRegression
slr = LinearRegression()
slr.fit(X, y)
y_pred = slr.predict(X)
print('기울기: %.3f' % slr.coef_[0])
print('절편: %.3f' % slr.intercept_)코드 실행시켜보면 절편이 아까처럼 0이 아닌데, 사이킷런의 LinearRegression을 표준화되지 않은 RM과 MEDV 변수에 훈련시키면 특성이 표준화되지 않았기 때문에 모델 가중치 달라진다.
아까처럼 RM에 대한 MEDV 그래프 그려서 보면
직접 만든 경사 하강법 구현과 비교하면 데이터 비슷하게 학습했다. 대체로 동일함
lin_regplot(X, y, slr)
plt.xlabel('Average number of rooms [RM]')
plt.ylabel('Price in $1000s [MEDV]')
# plt.savefig('images/10_07.png', dpi=300)
plt.show()RANSAC을 사용해 안정된 회귀 모델 훈련
선형 회귀모델은 outlier 라는 이상치에 크게 영향받는다.
이상치 제거 방식 대신 (사전 지식이 많이 필요하기 때문)
RANSAC 알고리즘 사용해 안정된 회귀 모델 봐볼것임 .
- RANSAC 알고리즘 (RANdom SAmple Consensus) : 정상치(inlier)라는 일부 데이터로 회귀 모델 훈련.
랜덤하게 일부 샘플 정상치로 선택, 모델 훈련 -> 훈련 모델에서 다른 모든 포인트 테스트 (사용자 입력 허용오차 하에서) -> 모든 정상치 사용해 모델 다시 훈련 -> 훈련 모델과 정상치 간 오차 추정 -> 성능이 사용자 지정 임계값 도달 or 지정 반복 횟수까지 도달하면 알고리즘 종료 or not 다시 처음부터
from sklearn.linear_model import RANSACRegressor
ransac = RANSACRegressor(LinearRegression(),
max_trials=100,
min_samples=50,
loss='absolute_error',
residual_threshold=5.0,
random_state=0)
ransac.fit(X, y)
inlier_mask = ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)
line_X = np.arange(3, 10, 1)
line_y_ransac = ransac.predict(line_X[:, np.newaxis])
plt.scatter(X[inlier_mask], y[inlier_mask],
c='steelblue', edgecolor='white',
marker='o', label='Inliers')
plt.scatter(X[outlier_mask], y[outlier_mask],
c='limegreen', edgecolor='white',
marker='s', label='Outliers')
plt.plot(line_X, line_y_ransac, color='black', lw=2)
plt.xlabel('Average number of rooms [RM]')
plt.ylabel('Price in $1000s [MEDV]')
plt.legend(loc='upper left')
# plt.savefig('images/10_08.png', dpi=300)
plt.show()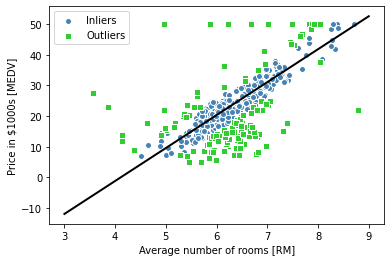
RANSAC을 사용한 것과 사용하지 않은 것 (이전 절) 이 차이가 존재하긴 함
RANSAC 사용하면 데이터셋 이상치 잠재적 영향 감소시킨다. 그렇지만 데이엍 예측 성능에 긍정적 영향 있는지 알지 못함.
그렇다면 예측 모델 시스템 구축하는 중요한 부분인 회귀 모델 평가하는 방법이 없을까 ? 있지 당근
선형 회귀 모델의 성능 평가
데이터셋에 있는 모든 변수 사용해 다변량 회귀 모델을 한번 훈련해본다.
from sklearn.model_selection import train_test_split
X = df.iloc[:, :-1].values
y = df['MEDV'].values
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.3, random_state=0)
slr = LinearRegression()
slr.fit(X_train, y_train)
y_train_pred = slr.predict(X_train)
y_test_pred = slr.predict(X_test)모델이 여러 특성을 사용하기 때문에 2차원 그래프로 선형 회귀 직선 못그린다. 그래서 잔차 대 예측값 그래프 (= 실제 값과 예측 값 사이의 차이 또는 수직거리) 그래프를 그릴 수 있음.
모델 성능 정량적으로 측정하는 방법 1 : 잔차 그래프
그래프 그려보는 코드는
plt.scatter(y_train_pred, y_train_pred - y_train,
c='steelblue', marker='o', edgecolor='white',
label='Training data')
plt.scatter(y_test_pred, y_test_pred - y_test,
c='limegreen', marker='s', edgecolor='white',
label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, color='black', lw=2)
plt.xlim([-10, 50])
plt.tight_layout()
# plt.savefig('images/10_09.png', dpi=300)
plt.show()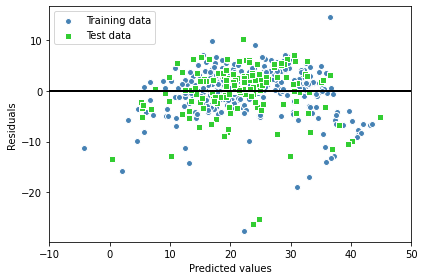
좋은 회귀 모델은 오차가 랜덤하게 분포되고, 잔차는 중앙선 주변으로 랜덤하게 흩어져야함.
잔차 그래프에서 패턴 나타나면 좋은 회귀 모델이 아니다.
잔차 그래프 사용해 이상치도 감지 가능하다.
모델 성능 정량적으로 측정하는 방법 2 : 평균 제곱 오차 (MSE)
from sklearn.metrics import mean_squared_error
print('훈련 MSE: %.3f, 테스트 MSE: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
print('훈련 R^2: %.3f, 테스트 R^2: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))출력 결과는 훈련 데이터셋 mse 는 19.96 이고 테스트 데이터셋 mse 는 27.20이다. 이는 모델이 훈련 데이터셋에 과대 적합되었다는 신호다!

짚고 넘어갈것
- 훈련 mse 보다 테스트 mse가 훨씬 크면 훈련 데이터셋에 과대적합되었다는 신호
근데 mse는 값에 제한이 없다 (단위가 1000이라서 1000 곱하지 않은 데이터가 더 낮은 mse 만든다)
그래서 결정계수가 더 유용할 수 있다. (mse 표준화 버전 )
모델 성능 정량적으로 측정하는 방법 3 : 결정계수 (R^2)
결정계수(coefficient of determination, R^2) : 타깃의 분산에서 모델이 잡아낸 비율
R^2 = 1 - {MSE/V(y) }
R^2은 0에서 1사이 값 가지고, R^2=1이면 MSE=0이고 데이터 완벽 학습 했다는 것 (실무에서 이럴 일은 없지만..^^)
회귀에 규제 적용
규제는 부가 정보를 손실에 더해 과대적합 문제를 방지하는 방법이다.
복잡도에 대한 패널티 유도해 모델 파라미터 값 감소시키는 방법으로 선형 회귀 규제 방법 중 유명한건
- 릿지 회귀
- 라쏘
- 엘라스틱 넷
이다.
릿지 회귀
: 단순히 최소 제곱 비용 함수에 가중치의 제곱합 추가한 L2 규제 모델, 하이퍼파라미터 람다λ 증가시키면 규제 강도 증가되고, 모델 가중치 값 감소. 절편은 규제X
라쏘
: 규제 강도 따라 가중치 0 가능. 지도학습 특성 선택 기법으로 사용가능. 라쏘의 L1 패널티는 모델 가중치의 절댓값 합으로 정의
m>n (n : 훈련 샘플 개수, m : 가중치 개수) 인 경우 최대 n개의 특성 선택이 한계이다. 모델이 포화되는걸 피해서 라쏘의 성질이 유용하나 일부 애플리케이션에서는 도움안됨
- 모델 포화 : 훈련 샘플 개수가 특성 개수와 동일할 때 발생, 과모수화(overparameterization)의 한 형태.
엘라스틱 넷
: 라쏘와 릿지 회귀 절충안, 희소 모델 만들기위한 L1 패널티와 m>n 일 때 n보다 많은 특성 선택할 수 있는 L2 패널티 가짐
이러한 규제 선형 모델 사이킷런에 있느냐? -> 있음
하이퍼파라미터 λ 사용해 규제 강도 지정하는것만 제외하고 보통 회귀 모델과 사용법 비슷.
릿지 회귀:
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.0)리쏘 회귀:
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1.0)엘라스틱 넷 회귀:
from sklearn.linear_model import ElasticNet
elanet = ElasticNet(alpha=1.0, l1_ratio=0.5)선형 회귀 모델을 다항 회귀로 변환
특성과 타깃 관계가 선형이라는 가정이 어긋날 때 -> 다항식 항 추가해 다항 회귀 모델 사용
기존 데이터셋에 다항식 항 추가하고 다항 회귀 모델 훈련 법 알아보겠음
사이킷런 이용 다항식 항 추가
PolynomialFeatures 변환기 클래스 특성 한개인 간단 회귀 문제에 이차항 (d=2) 추가하는 방법
이차 다항식 추가하고
from sklearn.preprocessing import PolynomialFeatures
X = np.array([258.0, 270.0, 294.0,
320.0, 342.0, 368.0,
396.0, 446.0, 480.0, 586.0])\
[:, np.newaxis]
y = np.array([236.4, 234.4, 252.8,
298.6, 314.2, 342.2,
360.8, 368.0, 391.2,
390.8])
lr = LinearRegression()
pr = LinearRegression()
quadratic = PolynomialFeatures(degree=2)
X_quad = quadratic.fit_transform(X)
-> 비교 위해 그냥 선형 회귀 모델 훈련하고
--> 다항회귀 위해 변환 특성에서 다변량 회귀 모델 학습
---> 결과 그래프로 비교
# 선형 특성 학습
lr.fit(X, y)
X_fit = np.arange(250, 600, 10)[:, np.newaxis]
y_lin_fit = lr.predict(X_fit)
# 이차항 특성 학습
pr.fit(X_quad, y)
y_quad_fit = pr.predict(quadratic.fit_transform(X_fit))
# 결과 그래프
plt.scatter(X, y, label='Training points')
plt.plot(X_fit, y_lin_fit, label='Linear fit', linestyle='--')
plt.plot(X_fit, y_quad_fit, label='Quadratic fit')
plt.xlabel('Explanatory variable')
plt.ylabel('Predicted or known target values')
plt.legend(loc='upper left')
plt.tight_layout()
# plt.savefig('images/10_11.png', dpi=300)
plt.show()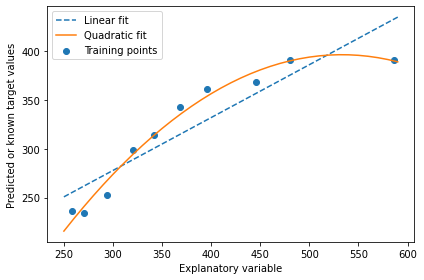
다항 회귀 모델이 선형 보다 특성과 타깃 사이 관계 잘 잡아낸 것을 볼 수 있음
평가 지표로서 2번 MSE와 3번 R^2 를 계산하면
y_lin_pred = lr.predict(X)
y_quad_pred = pr.predict(X_quad)
print('훈련 MSE 비교 - 선형 모델: %.3f, 다항 모델: %.3f' % (
mean_squared_error(y, y_lin_pred),
mean_squared_error(y, y_quad_pred)))
print('훈련 R^2 비교 - 선형 모델: %.3f, 다항 모델: %.3f' % (
r2_score(y, y_lin_pred),
r2_score(y, y_quad_pred)))
선형모델 mse 570에서 다항모델 61로 mse가 감소하고, 결정 계수를 봐도 다항모델 0.982가 선형모델 0.832 보다 잘 맞는 것을 보여준다.
랜덤 포레스트 사용해 비선형 관계 다루기
이제까지는 선형 관계를 다루고, 방금은 선형 관계 가정이 다르면 다항식을 추가햇지만, 이번에는 개별 선형 함수의 합으로 이해가능한
여러 개의 결정 트리를 앙상블한 랜덤 포레스트 회귀를 봐볼 것이다.
결정 트리 회귀
결정 트리 알고리즘 장점 : 비선형 데이터 다룰 때 특성 변환 불필요.
한번에 하나의 특성만 평가하기 때문이다. (가중치가 적용된 특성 조합을 고려한느 것이 아니라.)
결정 트리는 리프 노드가 순수 노드 되거나 종료 기준까지 반복적으로 노드 분할.
결정 트리 회귀에서 mse는 노드 내 분산이라고도 하는데, 분할 기준을 분산 감소로도 부른다.
사이킷런에서 DecisionTreeRegressor 클래스로 MEDV와 LSTAT 변수 간의 비선형 관계 모델링 해 결정 트리가 어떤 직선 학습하는 지 봐보자.
from sklearn.tree import DecisionTreeRegressor
X = df[['LSTAT']].values
y = df['MEDV'].values
tree = DecisionTreeRegressor(max_depth=3)
tree.fit(X, y)
sort_idx = X.flatten().argsort()
lin_regplot(X[sort_idx], y[sort_idx], tree)
plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000s [MEDV]')
# plt.savefig('images/10_14.png', dpi=300)
plt.show()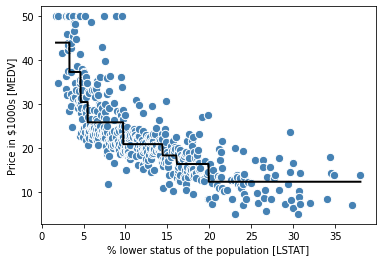
앞의 것만 보다보니 놀라운 그래프다.
결과 그래프에서 보이듯 결정 트리는 데이터의 일반적 경향 잡아낸다.
그러나 연속적이고 매끄러운 예측을 나타내지 못하는게 모델의 한계이다. 또 데이터에 과대적합되거나 과소 적합되지 않도록 적절한 트리 깊이 주의 깊게 선택이 필요하다. (여기서는 깊이 3이 좋은 선택)
그렇다면 결정 트리 회귀 말고 회귀 트리를 더 안정적으로 훈련 시킬 방법은 ? -> 랜덤 포레스트 회귀
랜덤 포레스트 회귀
랜덤 포레스트는 여러 개의 결정 트리를 연결한 앙상블방법이고, 일반적으로 단일 결정 트리보다 더 나은 일반화 성능을 낸다. (무작위성 때문, 모델의 분산 낮춰준다.)
랜덤 포레스트는 데이터 이상치에 덜 민감하고 하이퍼파라미터 튜닝이 많이 필요하지 않다는 장점도 가진다. (일반적 랜덤 포레스트 튜킹 하이퍼파라미터는 앙상블의 트리 개수)
회귀를 위한 기본적 랜덤 포레스트 알고리즘은 3장의 알고리즘과 거의 동일하고, 개별 결정 트리를 성장시키는데 mse 기준을 쓴다는 것만 차이가 있음.
타깃값 예측은 모든 결정 트리의 예측 평균해 계산함.
주택 데이터셋 이용 모든 특성 사용, 랜덤 포레스트 회귀모델 훈련
샘플 60:40으로 훈련:성능 평가 해보겠음
X = df.iloc[:, :-1].values
y = df['MEDV'].values
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.4, random_state=1)
from sklearn.ensemble import RandomForestRegressor
forest = RandomForestRegressor(n_estimators=1000,
criterion='squared_error',
random_state=1,
n_jobs=-1)
forest.fit(X_train, y_train)
y_train_pred = forest.predict(X_train)
y_test_pred = forest.predict(X_test)
print('훈련 MSE: %.3f, 테스트 MSE: %.3f' % (
mean_squared_error(y_train, y_train_pred),
mean_squared_error(y_test, y_test_pred)))
print('훈련 R^2: %.3f, 테스트 R^2: %.3f' % (
r2_score(y_train, y_train_pred),
r2_score(y_test, y_test_pred)))
랜덤 포레스는 훈련 데이터에 과대적합되는 경향 보이는데,
그래도 결정계수를 보면 0.878로 타깃과 특성 간의 관계 잘 설명하고있음.
예측 잔차도 확인해보면
plt.scatter(y_train_pred,
y_train_pred - y_train,
c='steelblue',
edgecolor='white',
marker='o',
s=35,
alpha=0.9,
label='Training data')
plt.scatter(y_test_pred,
y_test_pred - y_test,
c='limegreen',
edgecolor='white',
marker='s',
s=35,
alpha=0.9,
label='Test data')
plt.xlabel('Predicted values')
plt.ylabel('Residuals')
plt.legend(loc='upper left')
plt.hlines(y=0, xmin=-10, xmax=50, lw=2, color='black')
plt.xlim([-10, 50])
plt.tight_layout()
# plt.savefig('images/10_15.png', dpi=300)
plt.show()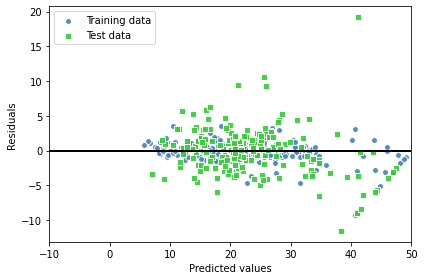
모델이 테스트 보다 훈련에 잘 맞는 것을 확인할 수 있고, 잔차 그래프도 보면 y 축 방향으로 테스트 데이터셋에 이상치가 보인다.
잔차 분포도 랜덤해 보이지 않는다.
이것으로 미루어 보아 모델이 특성의 정보를 모두 잡아낼 수 ㅇ벗다는 것을 나타낸다. 그렇다 하더라고 이전 장의 선형 모델 잔차그래프에 비교한다면 많이 개선된 것이라고 할 수 있다.
이상적인 오차는 랜덤하고 예측할 수 없어야하는데, (예측 오차가 특성 정보와 관계 없다) 특성의 정보가 잔차로 누설되어서 오차에 패턴이 감지된다.
해결 방법은 ?
랜덤 하지 않은 잔차 그래프 문제 다루는 보편적 방법은 없지만, 특성 변환하거나 학습 알고리즘 하이퍼파라미터를 튜닝해 모델을 향상시키는 등의 방법을 쓰거나, 더 간단하거나 더 복잡한 모델 선택하거나, 이상치 제거/ 추가특성 포함해 모델 성능을 높이던지의 방법을 사용한다.