트리

📌트리

• 비선형 구조
  → 관계를 가지는 원소들이 1 : n, n : n이다
• 원소들 간에 1 : n 관계를 가지는 자료구조
• 원소들 간에 계층관계를 가지는 계층형 자료구조
• 상위 원소에서 하위 원소로 내려가면서 확장되는 트리(나무) 모양의 구조

💡노드

• 트리의 원소

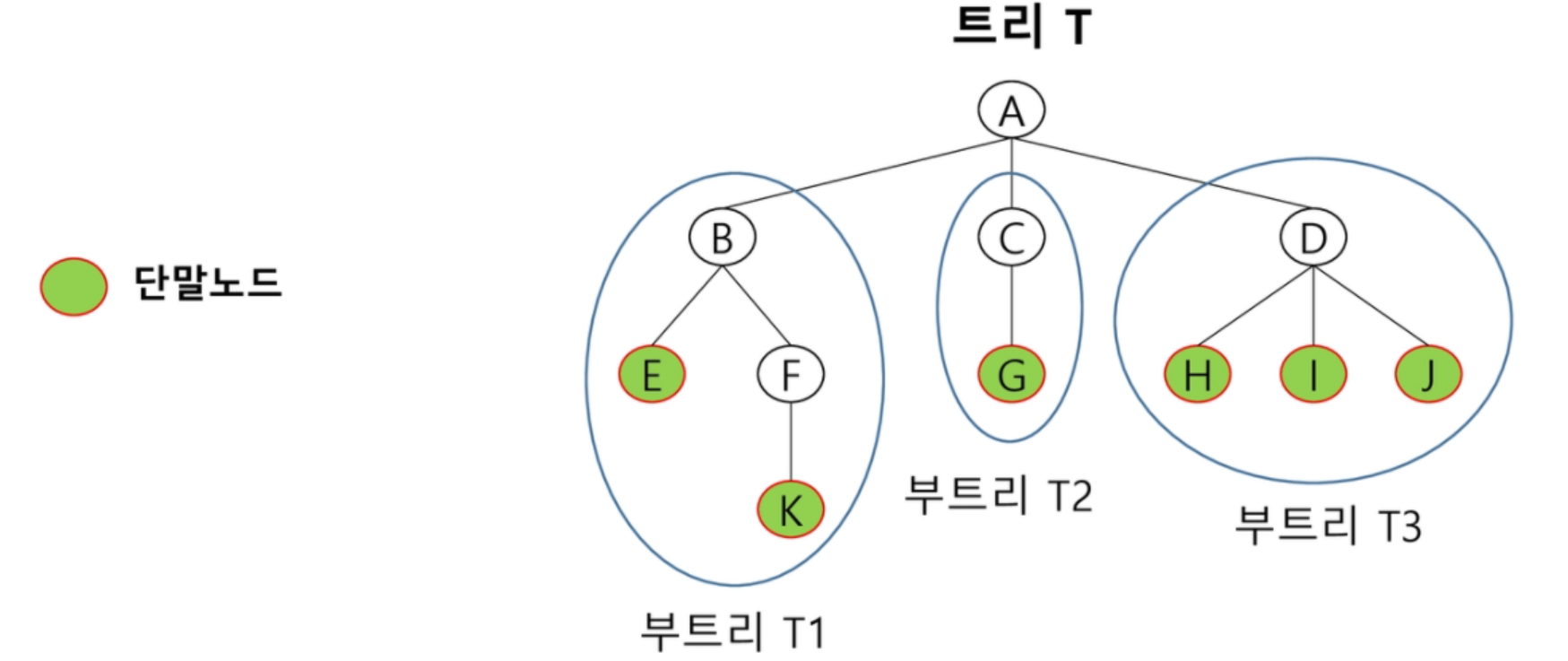
• 한 개 이상의 노드로 이루어진 유한 집합이며 다음 조건을 만족한다.

  1) 노드 중 최상위 노드를 루트(root)라고 부른다.
  2) 나머지 노드들은 n개의 분리 집합 T1, ... , TN으로 분리될 수 있다.

• 분리 집합들은 하나의 트리가 되며 루트의 부 트리(subtree) 라고 한다.

  

💡트리 용어 정리

• 간선
  • 노드와 노드를 연결하는 선으로 부모 노드와 자식 노드를 연결.
• 루트 노드
  • 트리의 시작 노드인 최상위 노드
• 형제 노드
  • 같은 부모 노드의 자식 노드들
• 조상 노드
  • 간선을 따라 루트 노드까지 이르는 경로에 있는 모든 노드들
• 서브 트리 (subtree)
  • 부모 노드와 연결된 간선을 끊었을 때 생성되는 트리
• 자손 노드
  • 서브 트리에 있는 하위 레벨의 노드들
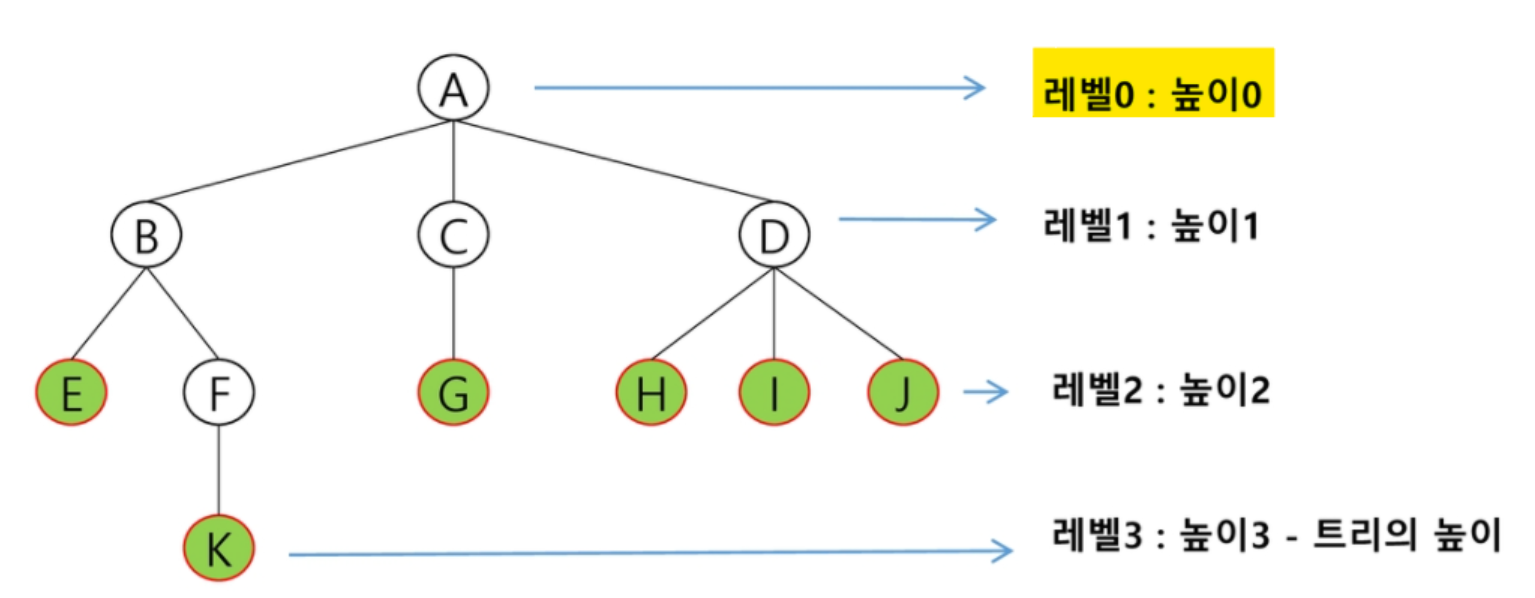
• 차수 (degree)
  • 노드의 차수 : 노드의 자식 노드의 수
  • 트리의 차수 : 트리에 있는 차수 중에서 가장 큰 값.
  • 단말 노드 : 차수가 0인 노드, 자식이 없는 노드
• 높이
  • 노드의 높이 : 루트에서 노드에 이르는 간선의 수. 노드의 레벨
  • 트리의 높이 : 노드의 높이 중 가장 큰 값. 최대 레벨

---

📌이진트리

• 차수가 2인 트리
• 각 노드가 자식 노드를 최대한 2개까지만 가질 수 있는 트리
• 모든 노드들이 최대 2개의 서브트리를 갖는 특별한 형태의 트리

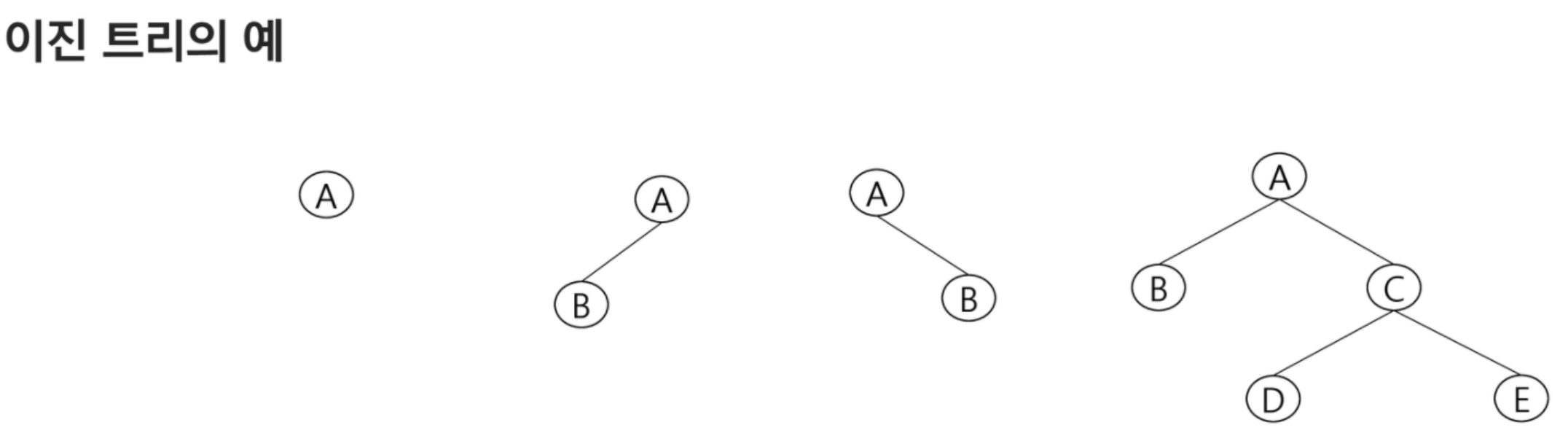
자식노드의 제한이 없다면 만들 수 있는 방법이 다양해 지지 않고
가변적으로 만들 수 밖에 없어서 비효율적.
자식의 노드 수를 제한해서 그 규칙을 통해 구현을 단순화 할 수 있다.

💡이진트리 특성

• 높이 n (레벨 n) 에서의 노드의 최대 개수 : 2ⁿ개
• 높이가 h인 이진 트리가 가질 수 있는 노드의 최소 개수는 h+1개, 최대 개수는 2^(h+1) -1개

💡이진트리 종류

◾ 포화 이진 트리 (Full Binary Tree)

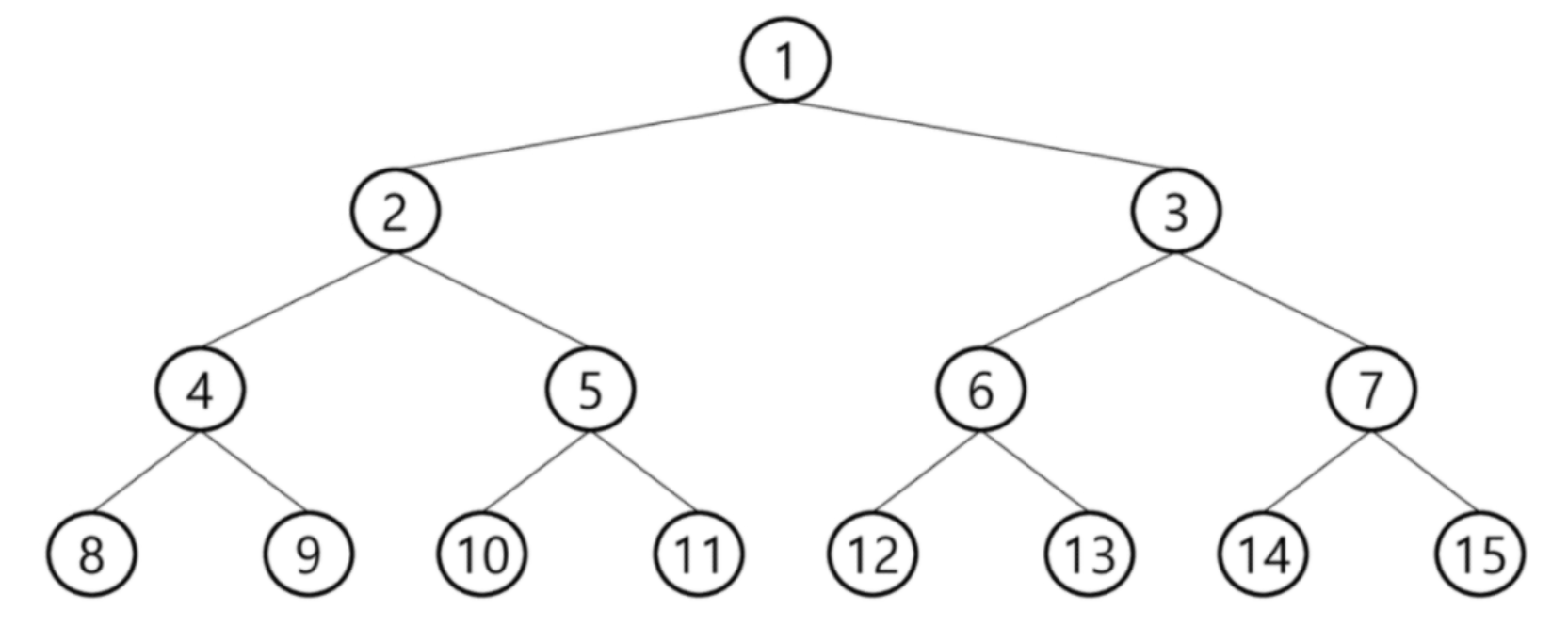
• 모든 레벨에 노드가 포화 상태로 차 있는 이진 트리
• 높이가 h일 때, 최대 노드개수인 2^(h+1) -1개의 노드를 가진 이진 트리
• 루트를 1번으로 하여 정해진 위치에 대한 노드 번호를 가짐

◾ 완전 이진 트리 (Complete Binary Tree)

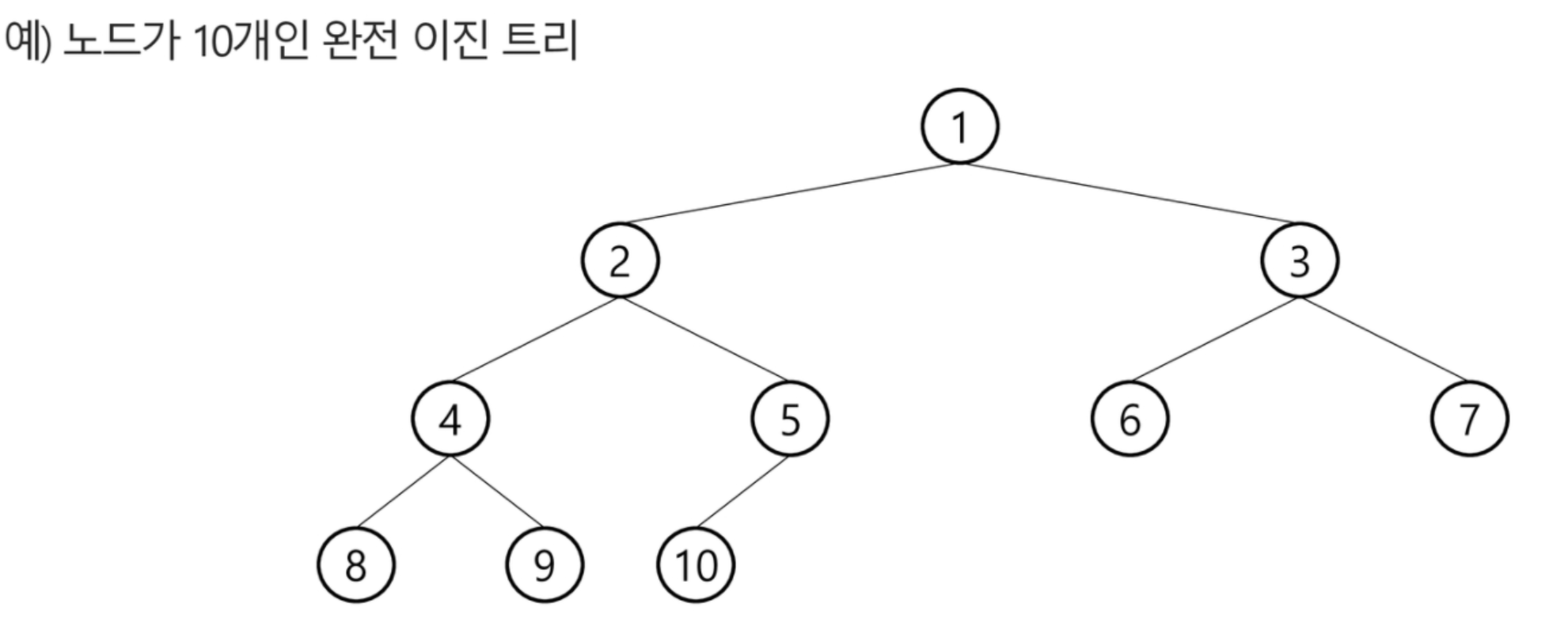
• 높이가 h, 노드 수가 n개 일 때,
  포화 이진 트리의 노드 번호 1번부터 n번까지 빈 자리가 없는 이진 트리

◾ 편향 이진 트리 (Skewed Binary Tree)

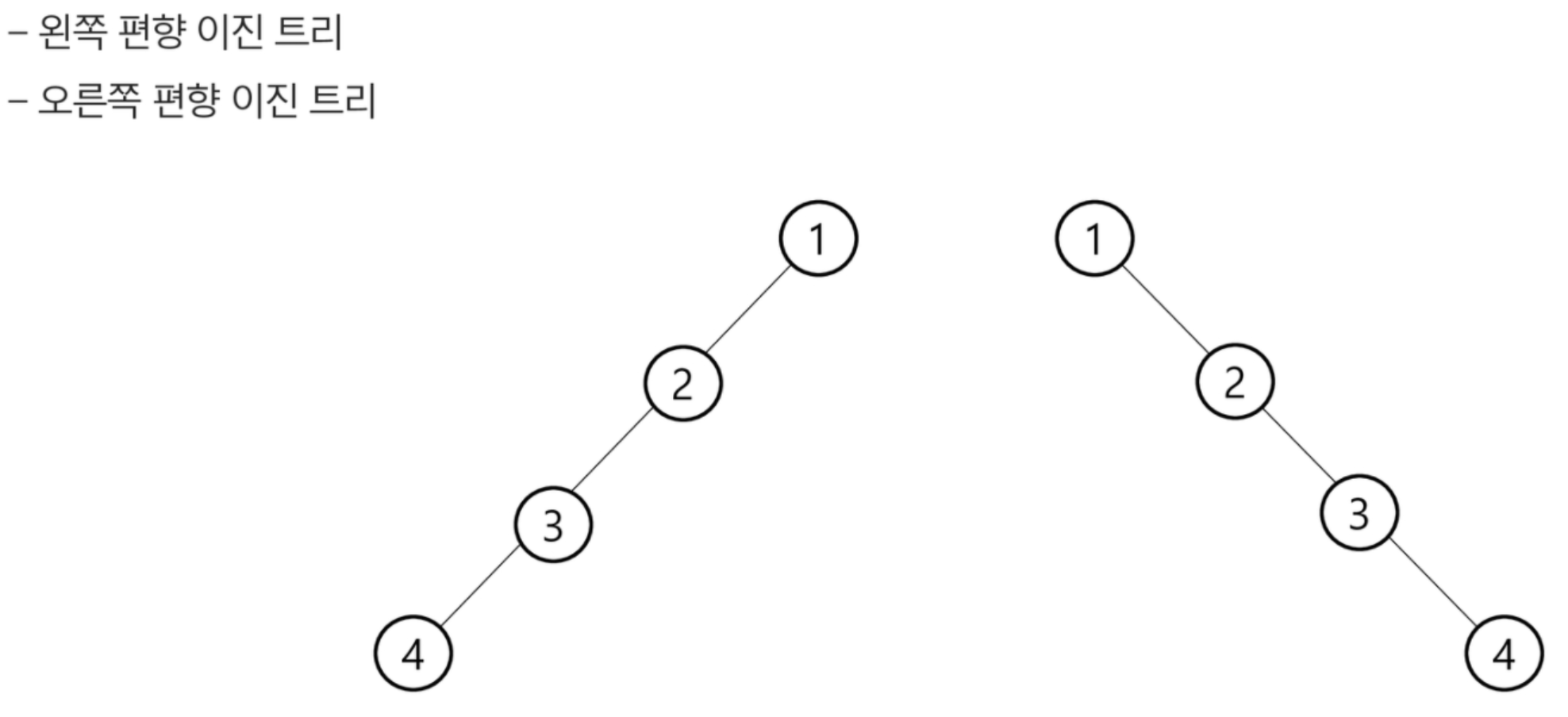
• 높이 h에 대한 최소 개수의 노드를 가지면서 한쪽 방향의 자식 노드만을 가진 이진 트리

---

💡배열을 이용한 이진 트리의 표현

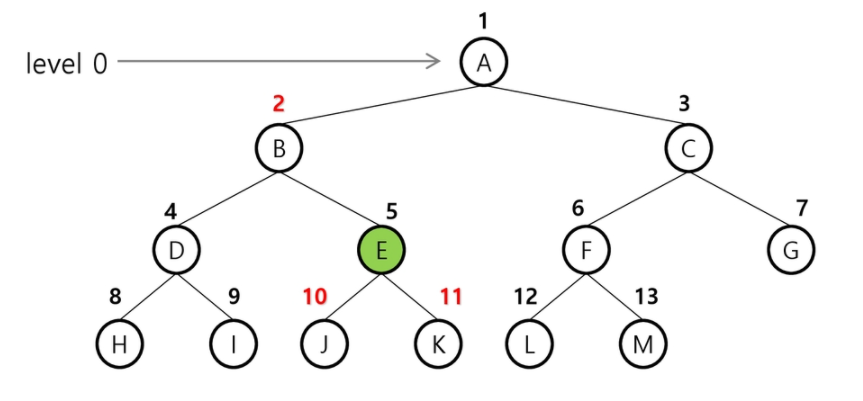
• 이진 트리에 노드 번호를 부여해서 논리적으로는 비선형 구조 트리로 사용하지만
  물리적으로는 배열에 넣어서 사용할 수 있다.

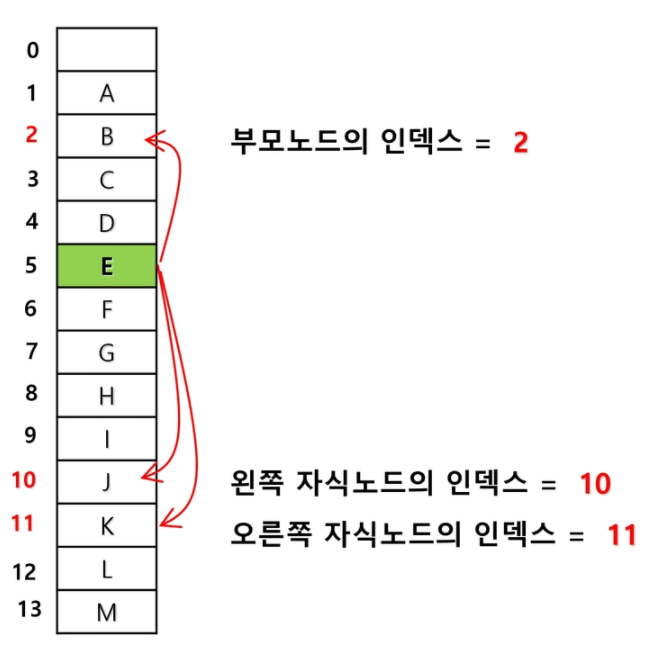
✔ 노드 번호의 성질

• 노드 번호가 i인 노드의 부모 노드 번호? -> i/2
• 노드 번호가 i인 노드의 왼쪽 자식 노드 번호? -> 2*i
• 노드 번호가 i인 노드의 오른쪽 자식 노드 번호? -> 2*i+1
• 레벨 n의 노드 번호 시작 번호는? -> 2ⁿ

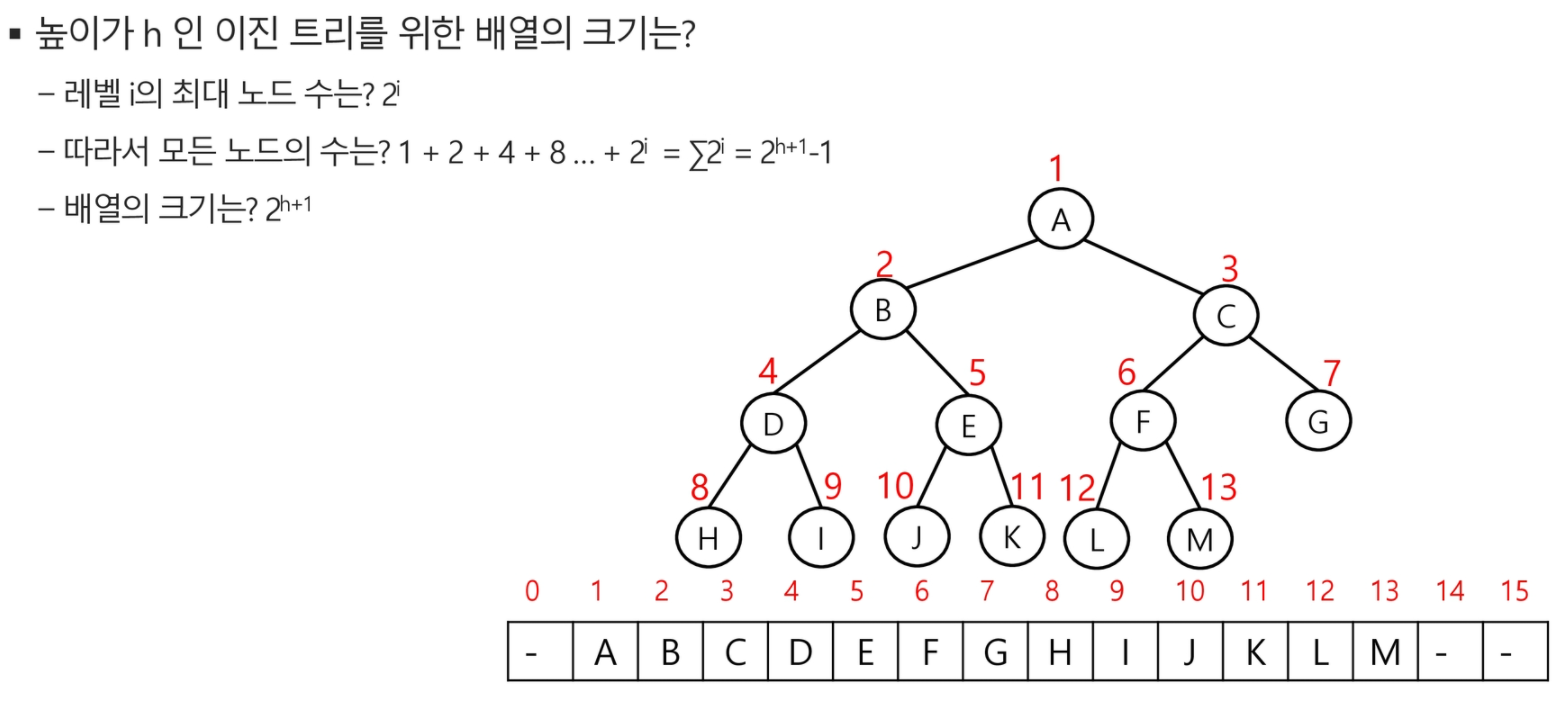
• 배열을 이용한 이진 트리의 표현의 단점

  • 편향 이진 트리의 경우에 사용하지 않는 배열 원소에 대한 메모리 공간 낭비 발생
  • 트리의 중간에 새로운 노드를 삽입하거나 기존의 노드를 삭제할 경우 배열의 크기 변경이 어렵다.