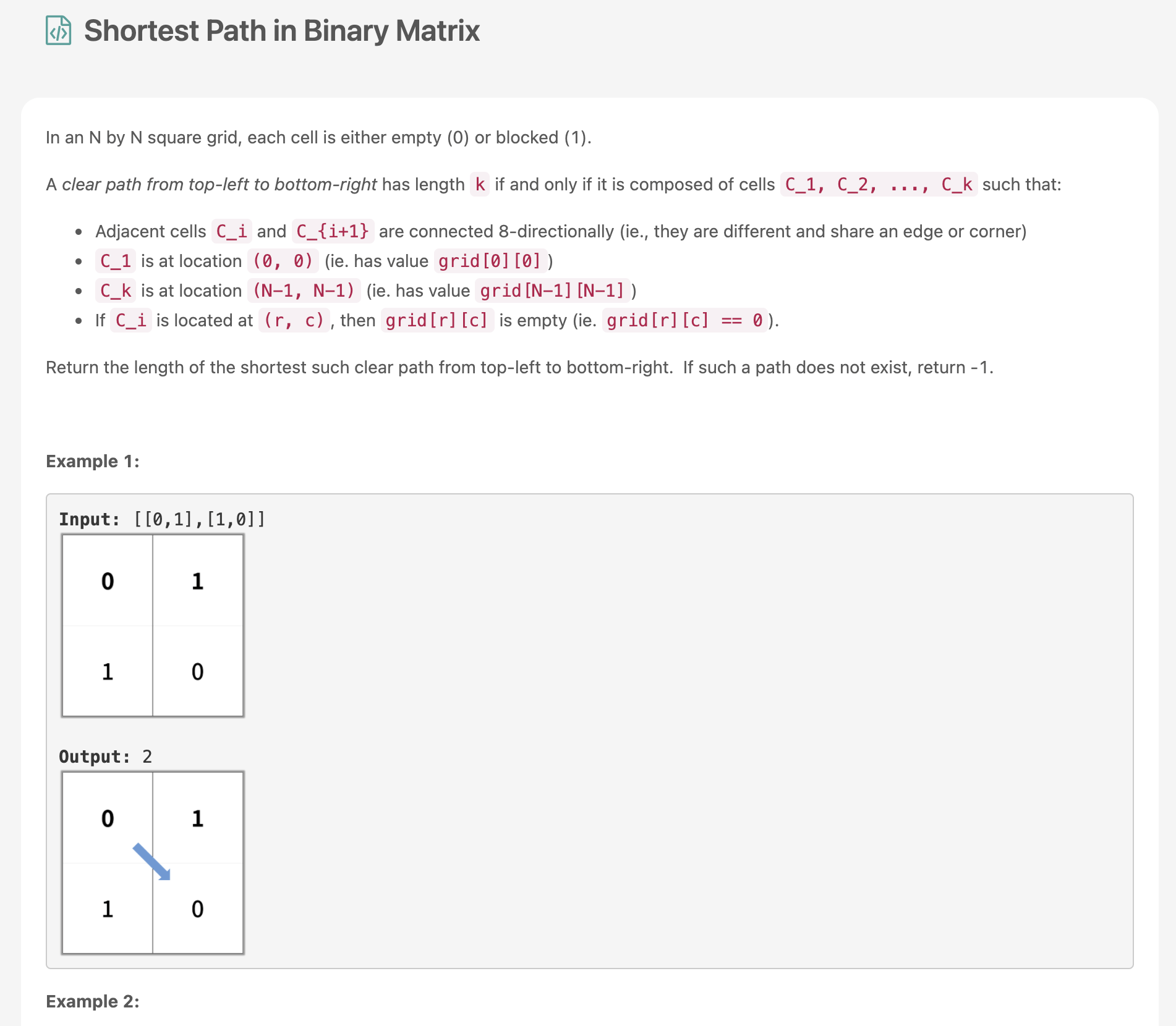
problem

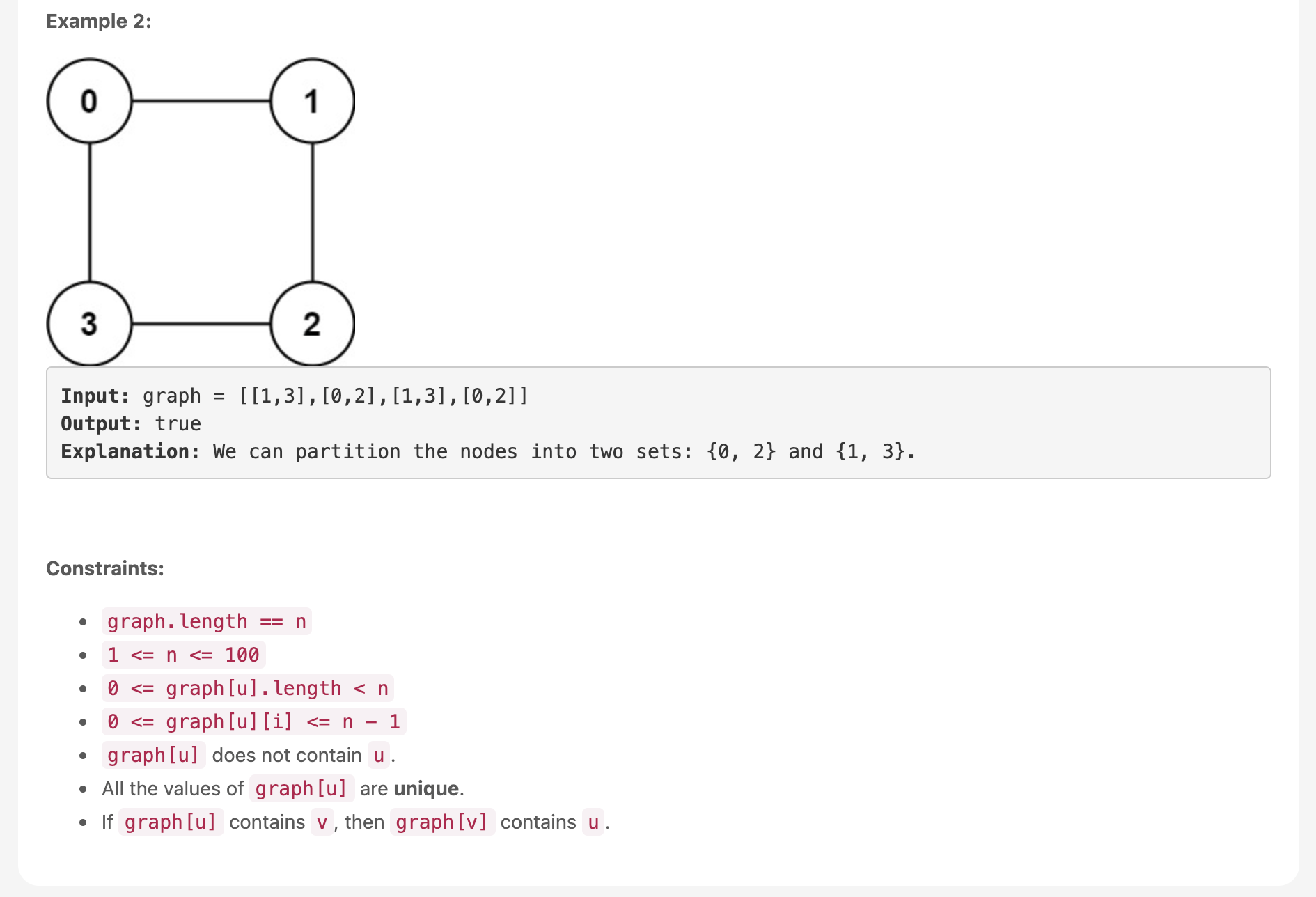
code
- node color == adjacent node color must be false for a graph to be a bipartite
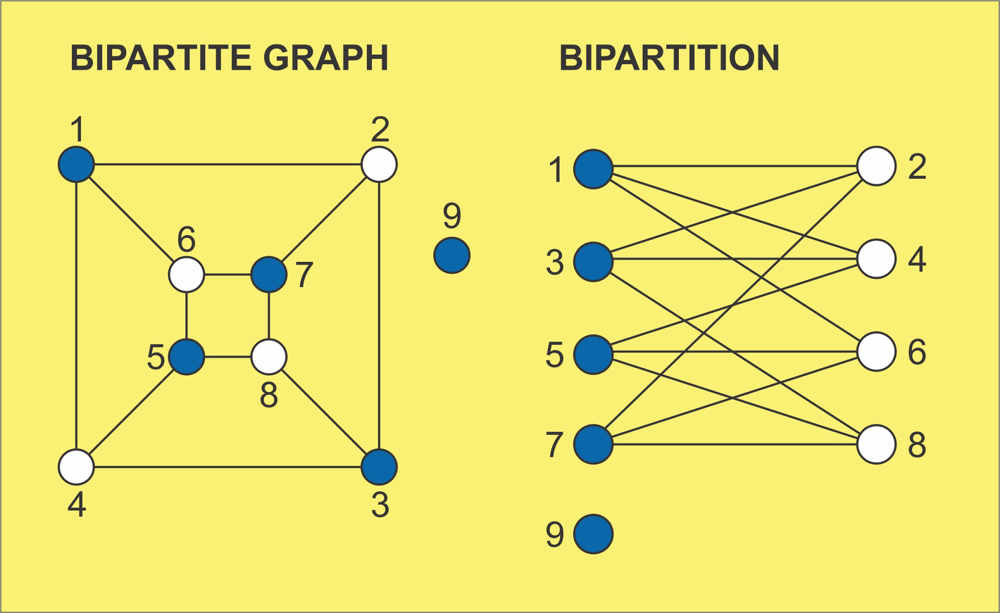
dfs w/o recursion
class Solution {
public boolean isBipartite(int[][] graph) {
int len = graph.length;
// 0: not yet
// 1: color white
// 2: color red
int[] visitedThenColor = new int[len];
Stack<Integer> s = new Stack<>();
for (int i = 0; i < len; i++)
{
if (visitedThenColor[i] != 0) continue;
visitedThenColor[i] = 1;
s.push(i);
while(s.size() > 0)
{
int curr = s.pop();
// There exists curr color marked, but not itered
// To use below, need both array for color and visited
// if (visitedThenColor[curr] != 0 ) continue;
for (int next : graph[curr])
{
if (visitedThenColor[next] == 0)
{
s.push(next);
visitedThenColor[next] = visitedThenColor[curr]^3;
}
else if (visitedThenColor[curr] == visitedThenColor[next])
{
return false;
}
}
}
}
return true;
}
}Time: O(N), iter every node in the graph once and iter its child once
Space: O(N), visitedThenColor + stack
explanation
- start node i if not visited, color be 1 for one group then push i to stack
- stack size 1 then
- while
- find adjacent nodes for node i, iter them
- check if visited, not then set color for the other group, push to stack
- if visited, then compare color between the node i and the adjecent
- same => false
- find adjacent nodes for node i, iter them
tip: 1^3 = 2, 2^3 = 1
why? XOR bitwise operation same: 0, diff: 1
3 <= 11
2 <= 10
1 <= 01
11^10 = 01 => 1
11^01 = 10 => 2how many element? 4 + 8, space? 4 + 8
[
[1,3],
[0,2],
[1,3],
[0,2]
]
START
for: i = 0, color=1, 0:push
while:
curr=graph[0],
for:
1:push,
3:push [3, 1]
stack:3, curr=graph[3], color=2,
for:
0:color1,
2:push [2, 1]
stack:2, curr=graph[2], color=1,
for:
1:push, 3
:color2! [1, 1]
stack:1, curr=graph[1], color=2,
for:
0:color1!,
2:color1! [1]
stack:1 curr=graph[1], color=1,
for:
1:color2!,
3:color2! []
*visitedThenColor= [1, 2, 1, 2]
for: i = 1
for: i = 2
for: i = 3
END
UF - Need to Study
class Solution {
int[] parent;
public boolean isBipartite(int[][] graph) {
int N = graph.length;
parent = new int[N];
for(int i = 0; i < N; i++)
parent[i] = i;
for(int i = 0; i < N; i++) {
for(int j = 0; j < graph[i].length; j++) {
if(find(i) == find(graph[i][j]))
return false;
union(graph[i][0], graph[i][j]);
}
}
return true;
}
private int find(int x) {
while(x != parent[x])
x = parent[x];
return x;
}
private void union(int x, int y) {
int parentX = find(x);
int parentY = find(y);
parent[parentY] = parentX;
}
}DFS with recursion
public boolean isBipartite(int[][] graph) {
int N = graph.length;
int[] colors = new int[N]; // 0 not colored, 1 = Red, -1 = Blue
for(int node = 0; node < N; node++)
if(colors[node] == 0 && !dfs(graph, node, 1, colors))
return false;
return true;
}
private boolean dfs(int[][] graph, int node, int color, int[] colors) {
if(colors[node] != 0)
return colors[node] == color;
colors[node] = color;
for(int adjNode : graph[node])
if(!dfs(graph, adjNode, -color, colors))
return false;
return true;
}
}