<BOJ 1931> 회의실 배정

pastafromvictoriadesert·2023년 3월 31일

boj 그리디 알고리즘 알고리즘

BOJ

목록 보기

1/12

백준 1931번 바로가기

📌그리디 알고리즘(Greedy Algorithm)

미래는 고민하지말고 현재 가장 최선인 선택을 하자

그리디 알고리즘은 현재 가장 최선인 방법만을 선택하고, 그것이 전체적으로도 최선이길 바라는 알고리즘 설계기법이다.

👉항상 옳은 결과만을 도출하는 것이 아니다.

직접 그림을 그려보았다

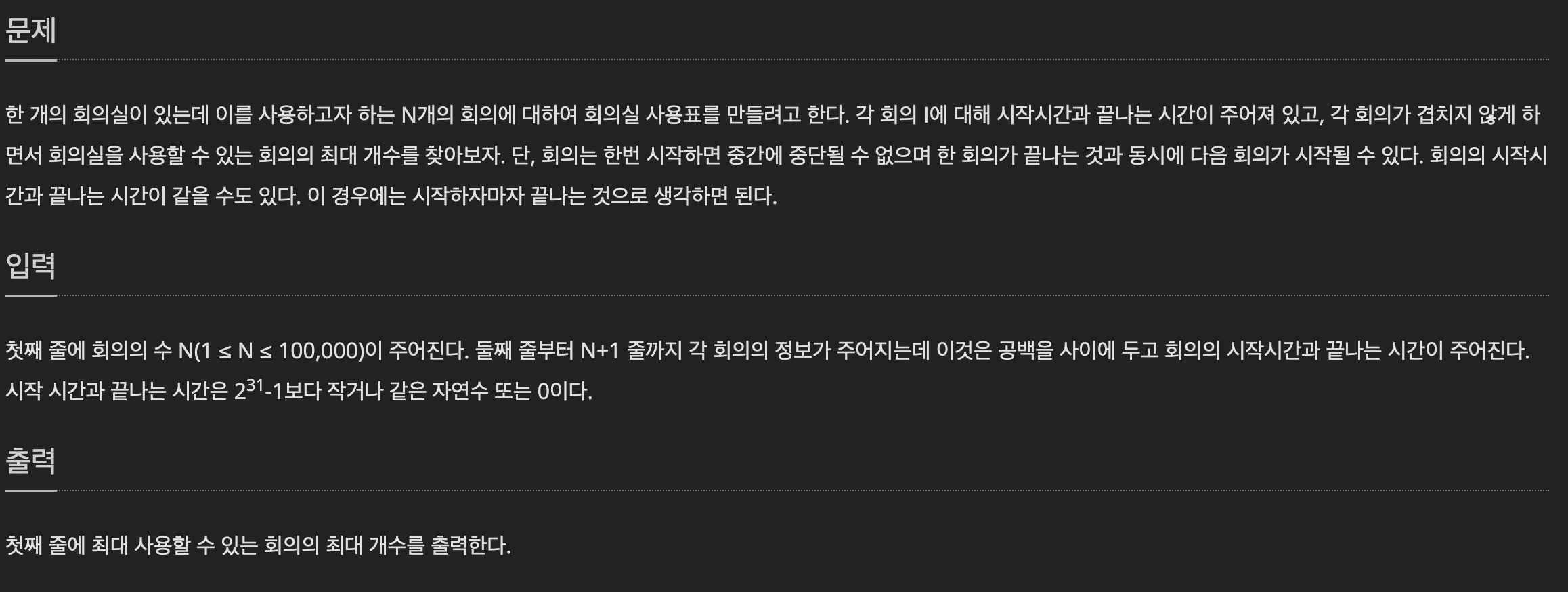
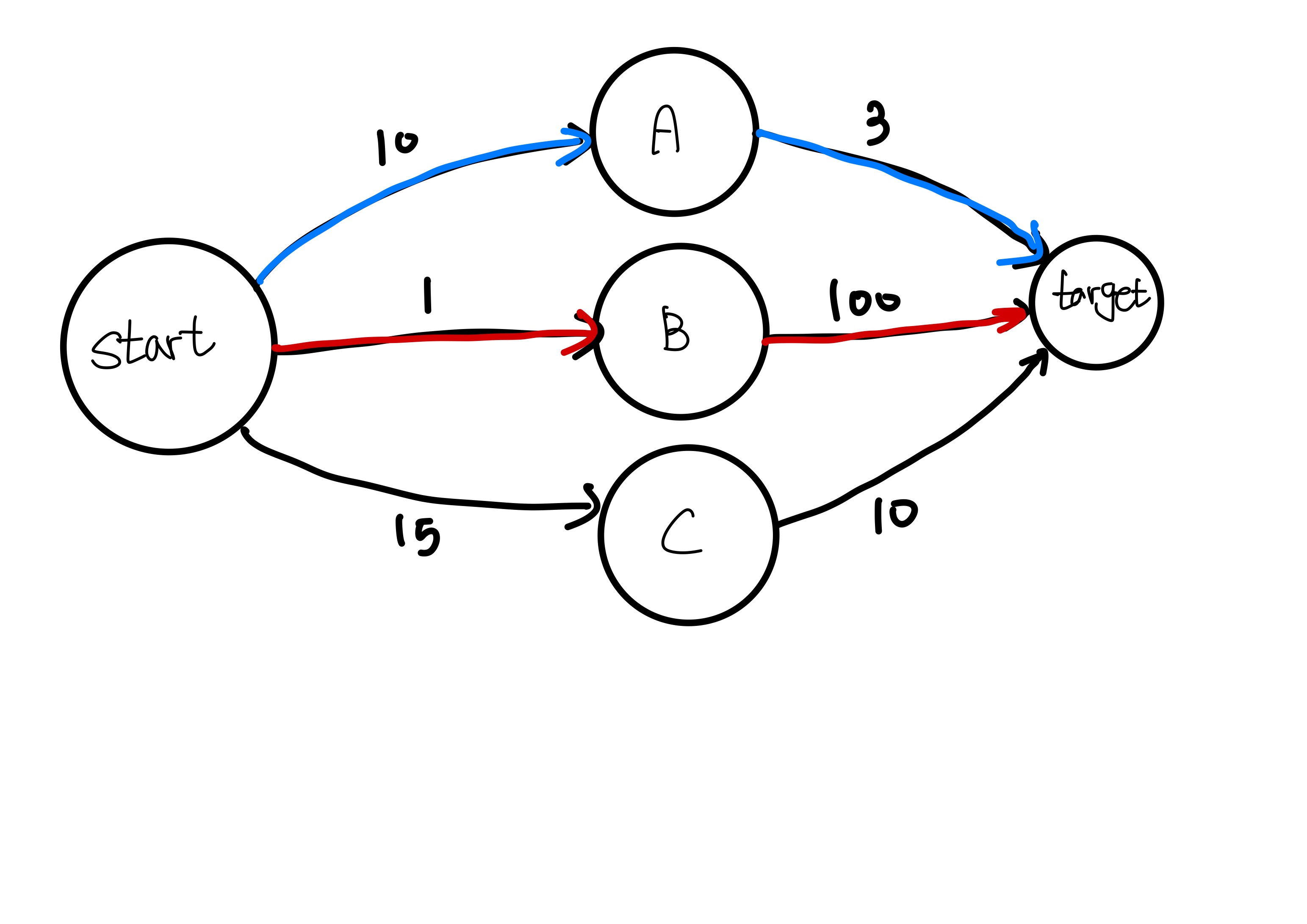
예를 들어, 위 그림처럼 start 에서 target으로 가는 최단경로를 찾을 때, 그리디 알고리즘을 이용한다면 빨간색의 경로로 이동할 것이다.

start에서 현재 비용이 가장 적은 경로를 선택해 B로 이동하고, B에서 target으로 이동 할 것이다.

하지만, 전체 비용이 가장 적게 드는 경로는 파란색이다.

👉이런 문제에서는 그리디 알고리즘을 사용한다면, 최적해를 구할 수 없다.

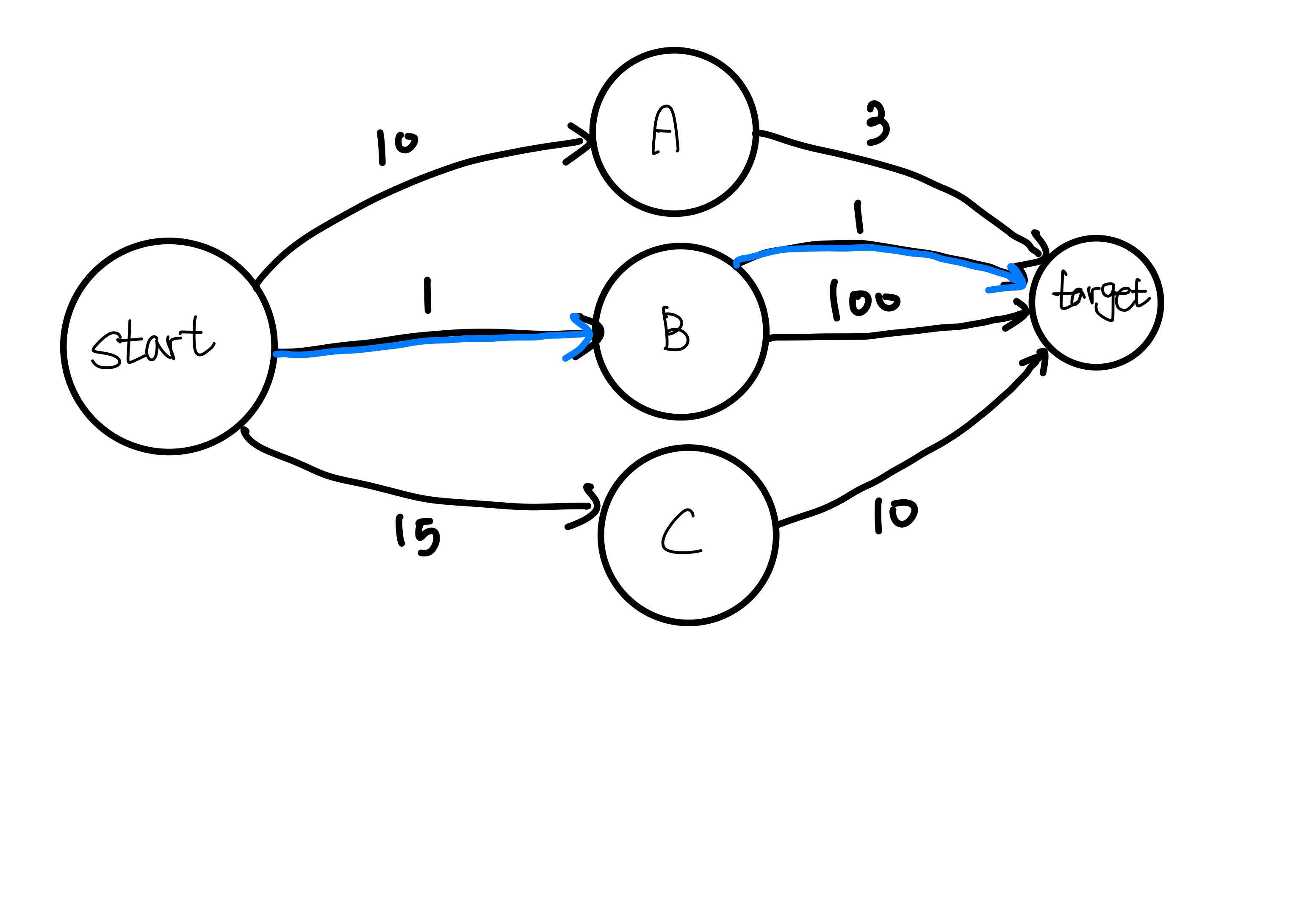
하지만 이번 그래프에서는 현재 가장 최선의 선택을 한다면 전체 상황에서도 최선인 상황이다.

👉 이렇게 그리디 알고리즘을 사용할 수 있는 상황에서만 사용해야한다.

📌백준 1931 회의실 배정

가장 대표적인 그리디 알고리즘 사용 문제이다.

회의의 수와 회의의 시작시간, 끝나는 시간이 주어진다.
이때, 회의가 겹치지 않게 회의실을 사용할 수 있는 회의의 최대 개수를 구하는 문제이다.

우선 한 회의가 끝나야 다음 회의를 진행할 수 있으므로, 회의가 끝나는 시간을 기준으로 오름차순 정렬 해주었다.

arr.sort(key=lambda x: x[1])

👉 arr 배열에 tuple 형태로 (시작시간, 끝나는시간)으로 저장되어 있다.

이렇게 정렬해주고 끝나는 시간에 맞춰서 다음 회의의 시작시간 중, 현재 회의의 끝나는 시간과 가장 가까운 값을 선택해주었다.

cnt = 1
temp = arr[0][1]
for a, b in arr[1:]: #처음 회의는 이미 cnt = 1에서 선택됨
    if temp <= a:
        cnt += 1
        temp = b

👉 정렬된 회의 중, 끝나는 시간이 가장 빠른 회의부터 선택한다.

끝나는 시간이 같은 경우는 ?

끝나는 시간이 같고 시작하는 시간이 다른경우에는 정렬이 제대로 되지 않는다.

👉끝나는 시간을 우선으로 정렬하되, 후순위로 시작하는 시간에 대해서도 정렬해주어야 한다.

arr.sort(key=lambda x: (x[1], x[0]))

정렬을 다시하면 정답이다.

전체코드

import sys
input = sys.stdin.readline

n = int(input())
arr = []
for i in range(n):
    a, b = map(int, input().split())
    arr.append((a, b))

arr.sort(key=lambda x: (x[1], x[0]))

cnt = 1
temp = arr[0][1]
for a, b in arr[1:]:
    if temp <= a:
        cnt += 1
        temp = b

if n == 1:
    print(1)
else: print(cnt)