📌다이나믹 프로그래밍(Dynamic Programming)
동적 계획법
하나의 큰 문제를 여러 개의 작은 문제로 나누고, 그 결과를 저장해 큰 문제를 해결할 때 사용하는 알고리즘 설계기법이다.
👉이미 계산했던 문제를 다시 계산하지 않으므로 시간복잡도를 효율적으로 개선할 수 있다.
이론적인 부분은 생략
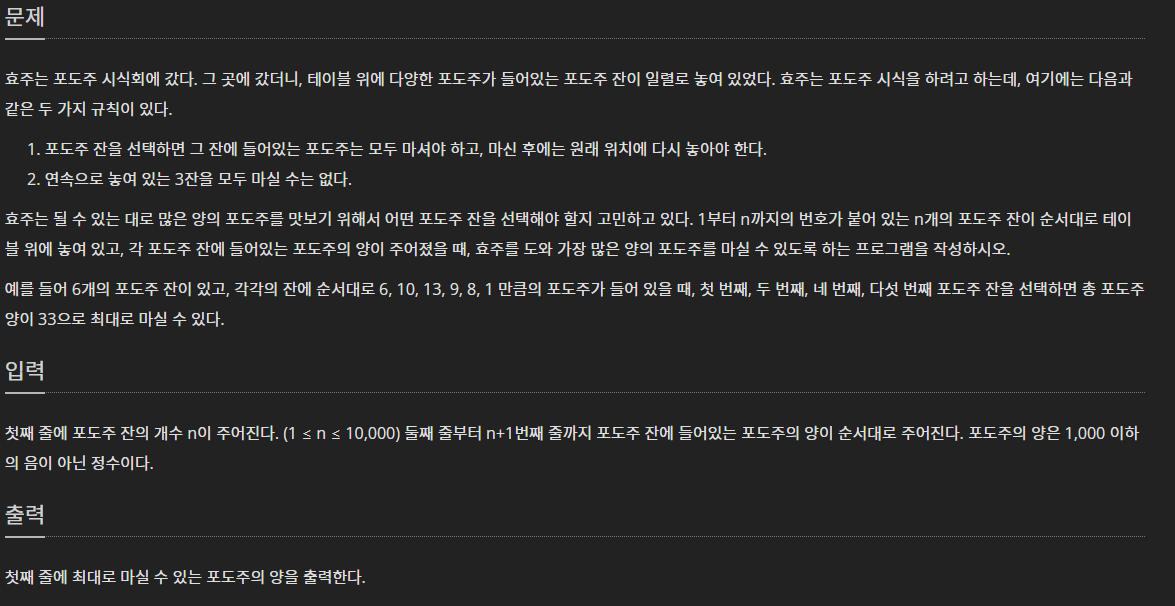
📌백준 2156 포도주 시식
포도주를 먹는 규칙 두 개 있다.
- 포도주 잔을 선택하면, 그 잔은 모두 비워야 하고, 제자리에 두어야 한다.
- 연속으로 놓여있는 3잔을 모두 마실 수 없다.
포도주의 개수 n과 각 포도주의 양이 주어질 때, 가장 많이 먹을 수 있는 포도주의 양을 구하는 문제이다.
모든 경우의 수를 다 검사하려면 엄청난 시간이 소요될 것 이다.
👉이전까지 먹은 포도주의 양을 저장하기 위한 테이블을 작성한다.
dp = [0 for i in range(n)]
dp[0] = arr[0]만약 포도주가 2잔 이하의 개수만큼만 있을 경우, 무조건 첫 잔을 먹어야 하기 때문에 dp테이블의 첫 번째 값을 초기화 해주었다.
dp[1] = dp[0] + arr[1]포도주가 두잔 있을 경우, 첫째 잔과 둘째 잔을 먹는것이 가장 많이 먹는 경우의 수 이기 때문에, dp 테이블을 초기화 해 주었다.
이제 포도주를 먹는 경우의 수를 점화식으로 표현해 본다.
- 현재 포도주와 이전 포도주를 먹는 경우, 전전 포도주는 먹을 수 없다.
dp[i] = dp[i-2] + arr[i]- 현재 포도주와 전전 포도주를 먹는 경우엔, 이전 포도주를 먹을 수 없다.
dp[i] = dp[i-3] + arr[i] + arr[i-1]- 이전 포도주와 전전 포도주를 먹고, 현재 포도주를 먹지 않는다.
dp[i] = dp[i-1]👉이제 위 세 가지 경우의 수 중 가장 큰 값이 현재 가장 많이 먹을 수 있는 포도주의 양 인 것이다.
전체코드
import sys
input = sys.stdin.readline
n = int(input())
arr = []
for i in range(n):
arr.append(int(input()))
dp = [0 for i in range(n)]
dp[0] = arr[0]
if n >= 2:
dp[1] = dp[0] + arr[1]
if n >= 3:
for i in range(2, n):
dp[i] = max(dp[i-2] + arr[i], dp[i-3] + arr[i] + arr[i-1])
dp[i] = max(dp[i], dp[i-1])
print(max(dp))
else:
print(arr[0])
📌고찰
- 탐색 문제에서는 많은 경우에 DP를 사용할 수 있다.
- 그렇기 때문에 DP에 익숙해져야 한다.
