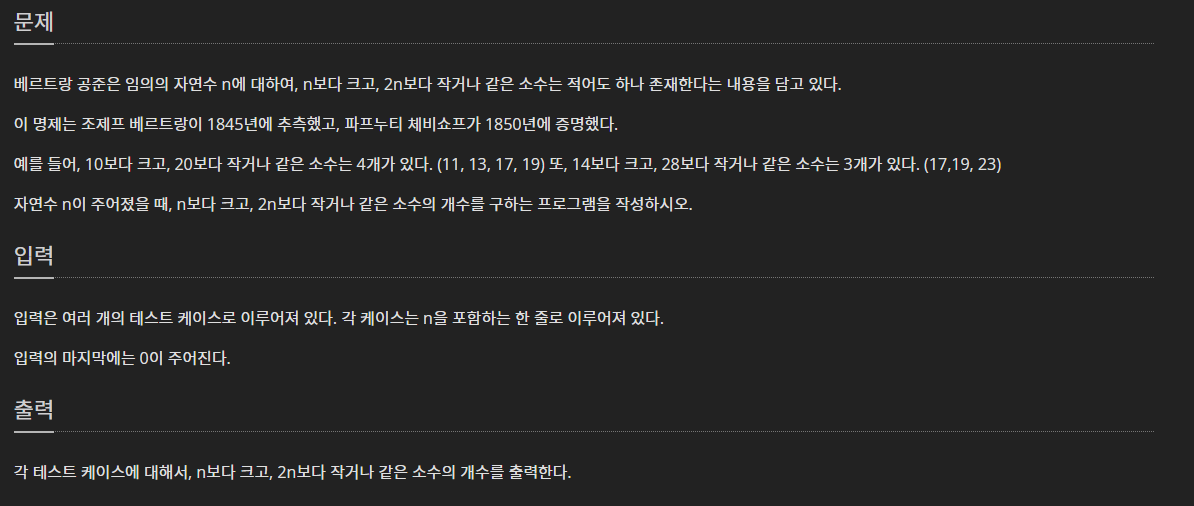
📌에라토스테네스의 체
가장 쉽고 유명한 소수구하기
기원전 200년부터 사용하던 소수를 구하는 알고리즘이다.
체로 걸러내듯 소수를 찾기 때문에 에라토스테네스의 체라는 이름이 붙었다.
로직은 다음과 같다.
- 2부터 소수를 구하고자 하는 범위의 수를 모두 적는다. (1은 소수가 아니다.)
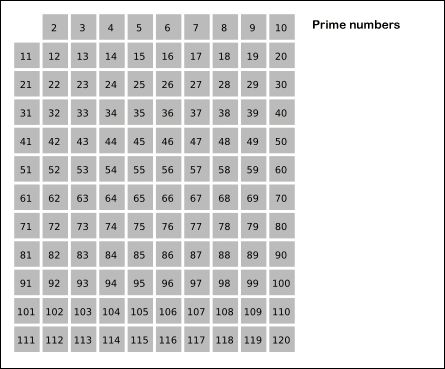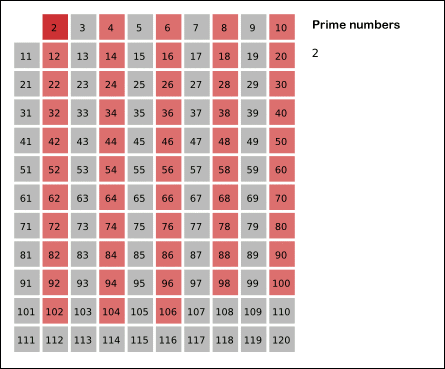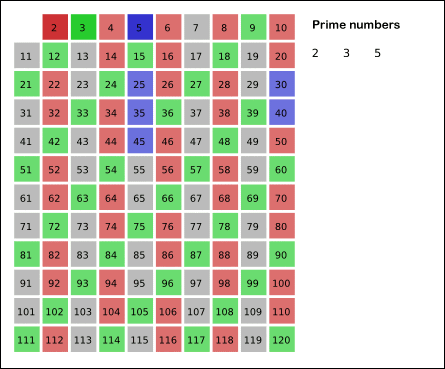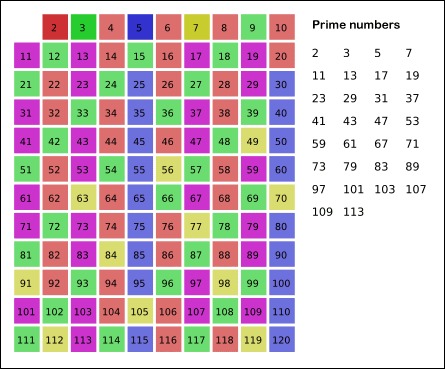
- 2는 소수이므로 2를 빼둔다.
- 자신을 제외한 자신의 배수를 모두 걸러낸다.
- 걸러지고 남은 수 중 3이 소수이므로, 3을 빼둔다.
- 똑같이 자신을 제외한 자신의 배수를 모두 걸러낸다.
- 남아있는 수도 위의 과정을 반복한다.
👉위의 GIF에서도 볼 수 있듯, 구하려는 범위의 수를 n 이라고 할 경우, √n 보다 작은 수의 배수들만 지워도 충분하다. (어차피 제곱수라서 앞에서 지워졌기 때문)
👉불필요한 탐색을 줄이기 위해서 굉장히 중요한 내용이다.
Python 코드
def prime_list(n):
# 에라토스테네스의 체 초기화: n개 요소에 True 설정(소수로 간주)
sieve = [True] * n
# n의 최대 약수가 sqrt(n) 이하이므로 i=sqrt(n)까지 검사
m = int(n ** 0.5)
for i in range(2, m + 1):
if sieve[i] == True: # i가 소수인 경우
for j in range(i+i, n, i): # i이후 i의 배수들을 False 판정
sieve[j] = False
# 소수 목록 산출
return [i for i in range(2, n) if sieve[i] == True]📌백준 4948 베르트랑 공준
수학적으로 증명된 베르트랑 공준에 대한 문제이다.
베르트랑 공준이란 임의의 자연수 n에 대하여 (n < k <= 2n)을 만족하는 소수 k가 적어도 한개 존재한다는 내용이다.
n이 주어지면, 소수 k의 개수를 구하는 문제이다.
우선 에라토스테네스의 체를 구현해 소수의 개수를 얻어야한다.
👉이 문제에서 n의 범위는 (1<= n <= 123,456) 이므로, 2*n까지의 소수를 미리 구해놓는다.
PrimeNum = [True for i in range(246913)] #123456 * 2 + 1
PrimeNum[0] = False
PrimeNum[1] = False
def eratos():
m = int(246913 ** 0.5) # 반복횟수를 줄이기위해서
for i in range(2, m+1):
if PrimeNum[i]:
for j in range(2*i, 246913, i):
PrimeNum[j] = False
그리고, n을 받을때마다 범위내에 소수가 몇개인지 세주고 출력해주면 된다.
문제에서 0이 입력될때 EOF라고 정했으므로, 0이 출력되면 반복문을 종료시킨다.
전체코드
import sys
input = sys.stdin.readline
PrimeNum = [True for i in range(246913)]
PrimeNum[0] = False
PrimeNum[1] = False
def eratos():
m = int(246913 ** 0.5)
for i in range(2, m+1):
if PrimeNum[i]:
for j in range(2*i, 246913, i):
PrimeNum[j] = False
eratos()
while 1:
n = int(input())
if not n:
break
cnt = 0
for i in range(n+1, 2*n+1):
if PrimeNum[i]:
cnt += 1
print(cnt)📌고찰
- 에라토스테네스의 체는 여러 문제에서 사용되므로, 꼭 익숙해져야한다.