그래프
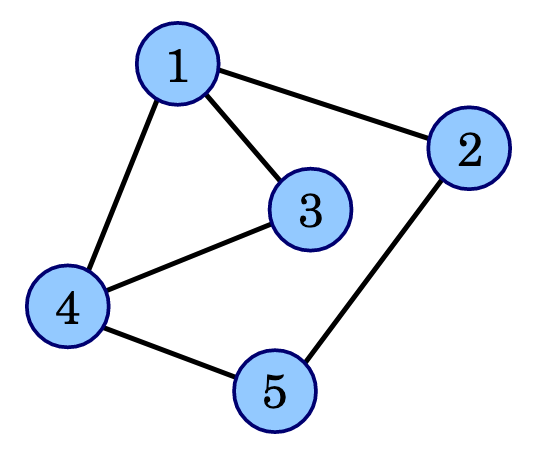
그래프는 노드나 노드들의 연결을 모은 것이다
앞에서 배운 트리는 그래프의 일종. 트리는 한 개의 노드(루트)에서 내려오는 여러 자식 노드의 형태.
그래프는 오늘날 매우 널리 쓰임. 모든 sns들이 그래프를 쓴다
영화추천 사이트, 쇼핑몰
넷플릭스나 아마존의 추천 알고리즘은 보통 데이터를 그래프 관계로 저장하는 것
‘좋아하실 만한 상품’, ‘이런것도 있습니다’
- Vertex - 노드를 가리키는 용어. 정점.
- Edge - 노드들 사이의 연결. 간선.
Weighted/Unweighted(가중/비가중)
가중은 연결, 즉 간선 자체에 부여된 값이 있는 것이다.
지도 그래프에 도로의 길이가 간선마다 부여되어 있는 것이 그 예이다.
Directed/Undirected(방향/무방향)
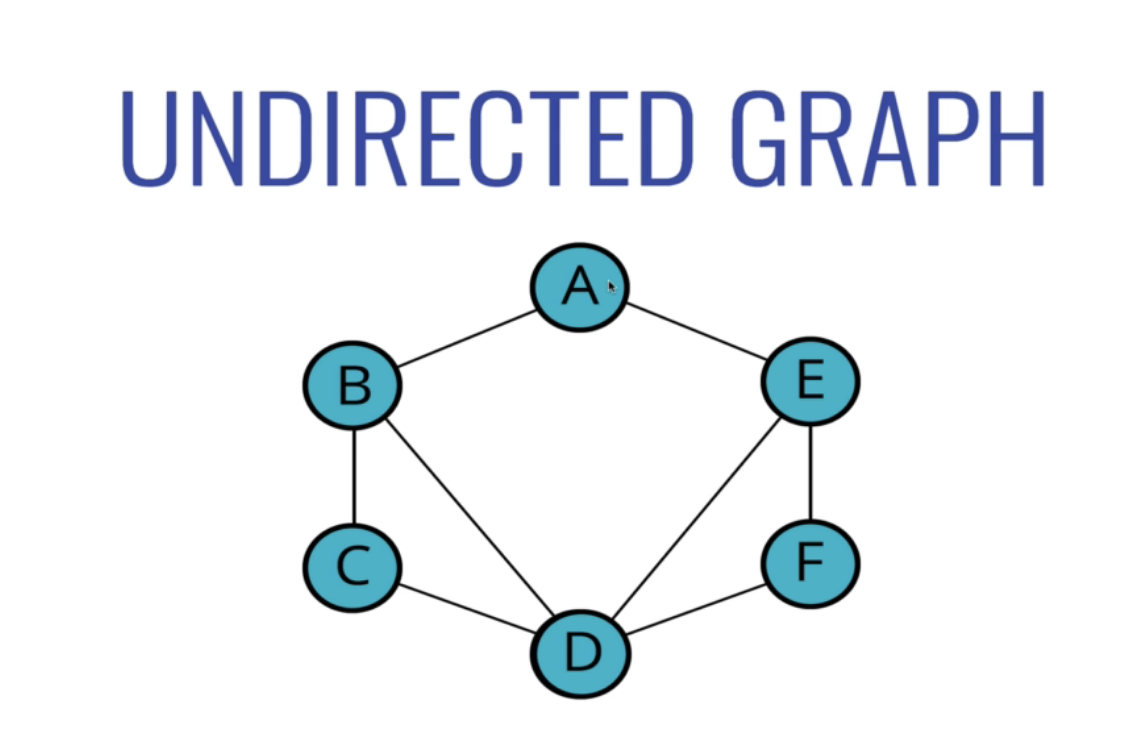
무방향 그래프에는 방향이나 양극 음극 따위가 없다.
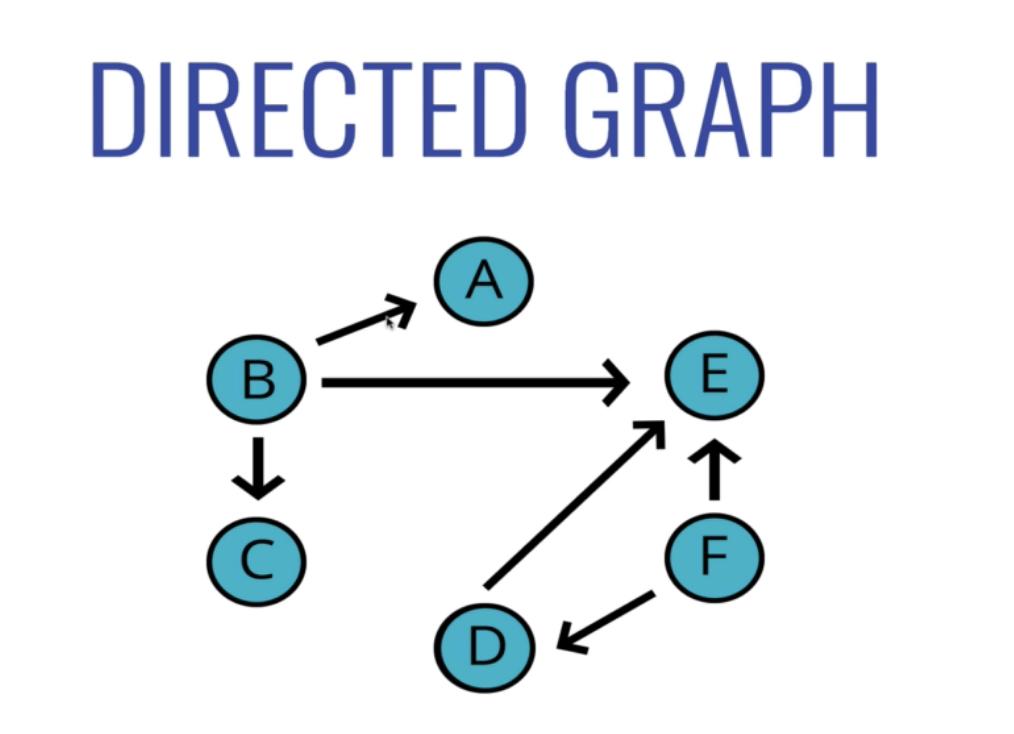
그에 비해 방향 그래프에는 연결, 즉 간선에 부여되는 방향이 있다. 한쪽 방향으로만 갈 수 있는 것이다.(sns에 팔로우 관계 모형)
Graph 구현 방식
배열이나 연결 리스트로 구현할 수 있다.
그래프를 구현하는 많은 방식이 있지만 기본적인 방법 두가지가 있다
- Adjacency Matrix 인접행렬
- Adjacency List 인접리스트
Adjacency Matrix 인접행렬
행렬은 이차원 구조로 보통 표현한다
각 노드들의 연결을 행렬로 표현한 것이다

A가 F와 B와 연결되어 있으므로 그 연결을 행렬상 1로 표시한다
이렇게해서 edge간선을 표현하는 것이다
Adjacency List 인접리스트
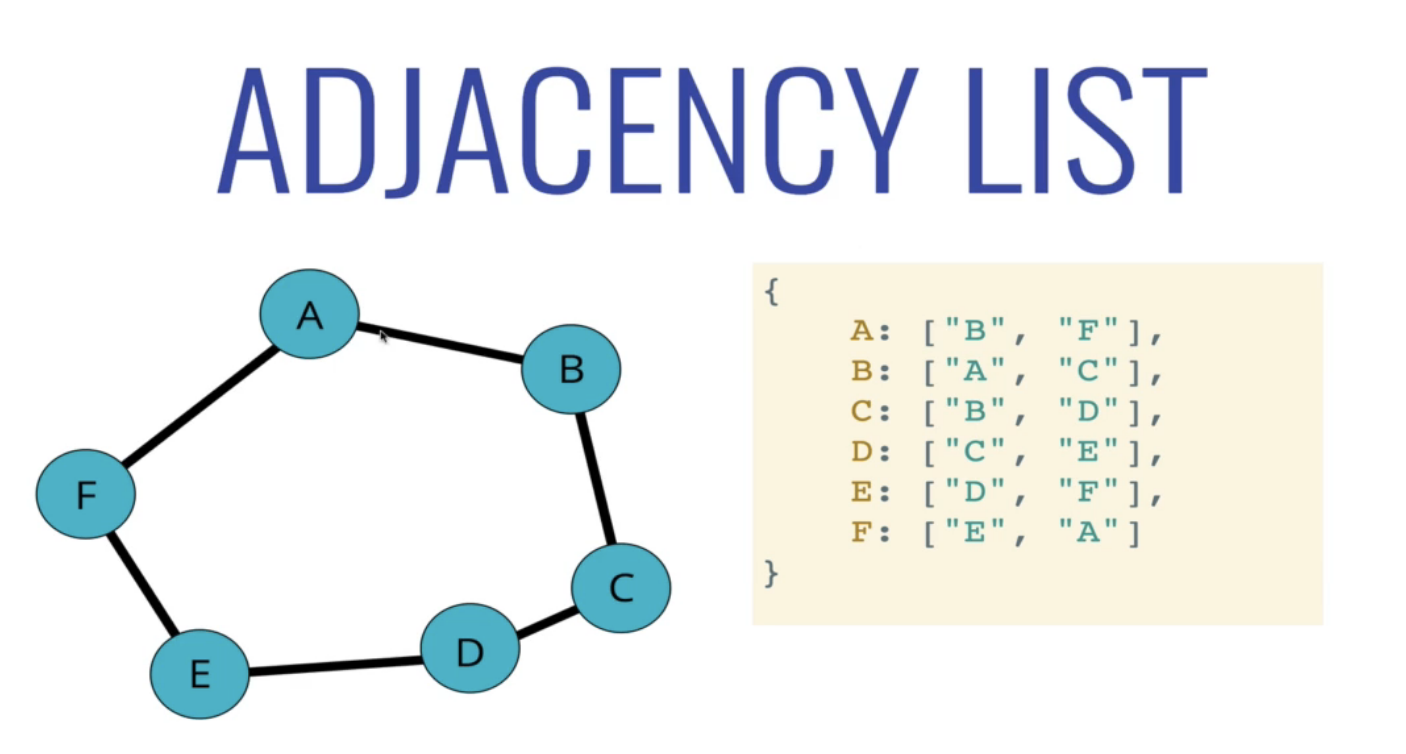
어떤 노드에 연결된 노드들을 해시테이블, 또는 숫자라면 배열에 리스트로 저장하는 방식
A를 보면 A에 연결된 B와 F가 들어있는 배열이 A키에 값으로 들어있는 것을 볼수있다
인접행렬과 인접리스트 비교
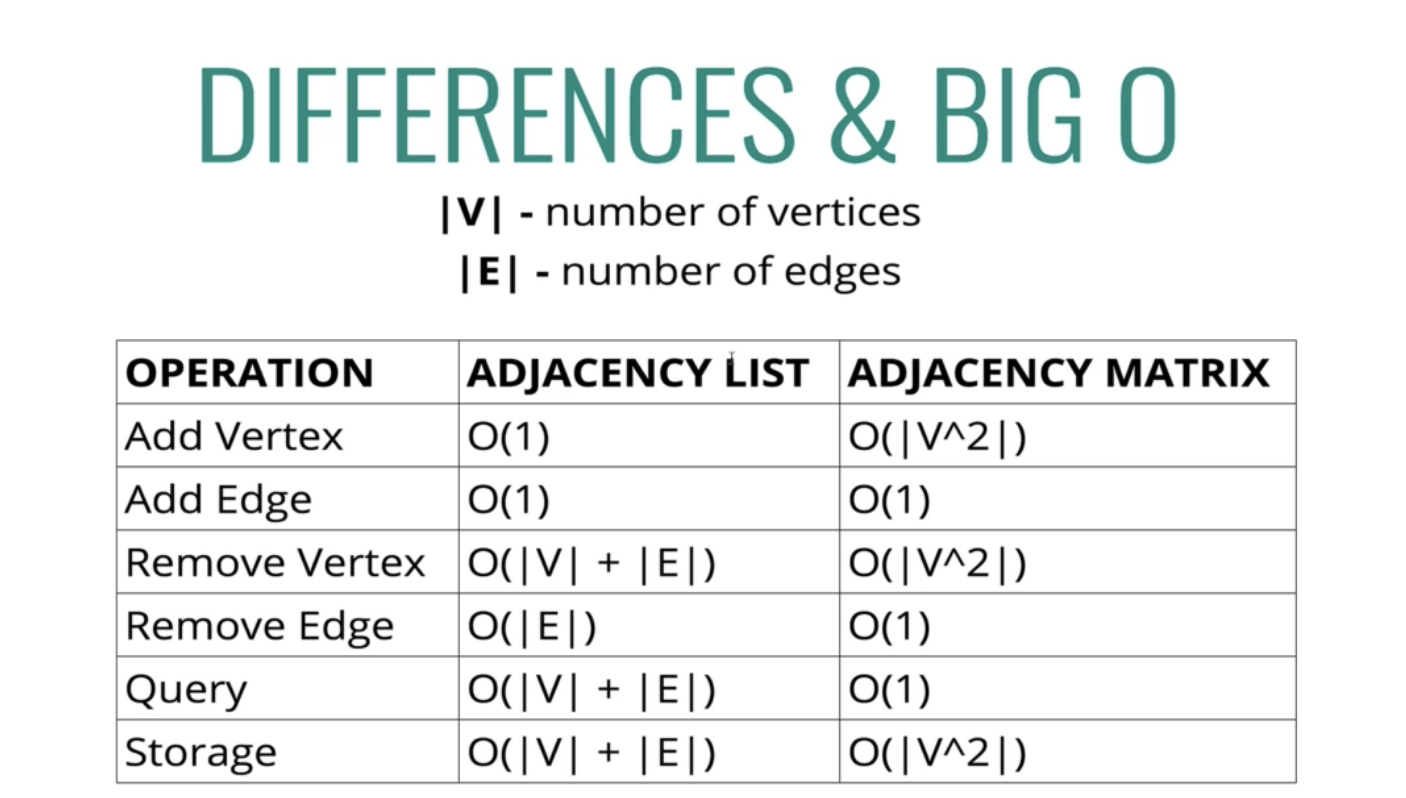
V는 정점의 개수, E는 정점의 개수이다
인접행렬에서 정점을 추가할때 V의 제곱을 빅오로 가지는 것은 행렬이 2차원구조이기 때문
새로운 정점 하나를 추가하면 한 칸을 더하는 것이 아니라 행에 한줄 추가, 열에도 한줄 추가되기 때문
인접리스트와 비교하면 인접리스트는 그냥 추가한 갯수만큼 커진다
행렬은 기본적으로 공간을 많이 차지한다. 존재하지 않는 간선도 0으로 전부 저장하니까.
인접리스트는 실제 간선만 저장한다
데이터가 퍼져있고, 연결 즉 간선이 많지 안으면 행렬을 사용하지 않는것이 낫다
인접리스트
- 인접행렬보다 더 적은 공간을 차지
- 모든 정점을 순회하는 것이 더 빠르다
- 특정 간선이 존재하는지를 확인하려면 느릴수 있다. → 이게 유일한 단점
인접행렬
- 더 많은 공간을 차지
- 순회하는 것도 느림
- 특정 간선이 존재하는지를 확인하는게 빠르다 → Query가 행렬의 장점
A와 D 사이에 간선이 있는가? 를 찾으려면 인접행렬에서는 바로 해당 칸을 찾아서 0인지 1인지 확인하면 된다
인접리스트에는 A로 간 다음에 리스트를 전부 순회해야 한다. 리스트가 아주 길면 루프에 시간이 오래걸린다.
인접리스트를 더 많이 사용한다.
현실의 데이터는 대부분 퍼져 있다. 정점의 개수는 많고 연결은 적기 때문에 인접리스트가 훨씬 효율적.
Graph 코딩
class Graph{
constructor(){
this.adjacencyList = {}; //연결리스트로 쓸 해시테이블. 객체.
}
addVertex(vertex){ // 그래프에 정점 추가하기
if(!this.adjacencyList[vertex]) this.adjacencyList[vertex] = []; // 해당 정점 이름을 키로, 빈 배열을 값으로 저장
}
addEdge(v1,v2){ // 두 정점 사이에 연결 추가하기
this.adjacencyList[v1].push(v2); // 해시테이블의 v1키 배열에다 v2를 넣고
this.adjacencyList[v2].push(v1); // v2에도 똑같이 해줌
}
removeEdge(vertex1,vertex2){ // 두 정점 사이에 연결 제거하기
this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(
v => v !== vertex2 // 필터를 써서 배열의 요소중 v2가 아닌것만 남기고 필터
);
this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(
v => v !== vertex1 // 필터를 써서 배열의 요소중 v2가 아닌것만 남기고 필터
);
}
removeVertex(vertex){ // 정점 자체를 삭제하기
while(this.adjacencyList[vertex].length){ // 해당 정점에 리스트를 삭제. 빈 배열될때까지 루프
const adjacentVertex = this.adjacencyList[vertex].pop(); //맨뒤 다른 정점을 pop한 후
this.removeEdge(vertex, adjacentVertex); // 해당 다른 정점과 삭제할 정점 2개 사이 연결을 위 연결제거하기 메서드로 삭제
}
delete this.adjacencyList[vertex] // 위 루프 다 돌면 빈 배열을 가진 정점이 남는다. 그걸 delete로 삭제.
}
}Graph Traversal 그래프 순회
그래프의 모든 노드를 다 방문하는 여러가지 방법
많은 경우 가장 가까운 노드 찾기, 가장 비슷한 노드 찾기, 또는 한 노드에서 다른 노드로 가는 최단 경로 찾기
어려운 알고리즘도 많다.
순회라고 하면 방문, 최신화, 확인, 탐색, 출력 등을 그래프의 모든 정점에 대해 수행하는 것.
그래프 순회가 사용되는 곳
- P2P 네트워크
- 웹크롤링
- 친구추천, 좋아할만한 상품 추천
- 최단경로 찾기
DFS(깊이 우선) 그래프 순회
그래프는 트리와 달리 위아래 방향이 명확하지 않다
그래프에서의 DFS는 인접점을 따라가고 따라가서 길이 막힐때까지 가는 것.
재귀형, 순환형으로 쓸 수 있다.
재귀적 용법의 DFS 그래프 순회
depthFirstRecursive(start){ // start는 시작할 노드
const result = []; // 최종결과를 저장할 리스트
const visited = {}; // 방문한 정점을 기록할 객체
const adjacencyList = this.adjacencyList; // 인접리스트
(function dfs(vertex){ // 헬퍼 메소드 재귀함수
if(!vertex) return null; //해당 노드의 인접리스트가 비어 있으면 null
visited[vertex] = true; // 일단 시작 노드는 방문했다고 기록.
result.push(vertex); // 결과 리스트에 Push
adjacencyList[vertex].forEach(neighbor => { //해당 노드의 인접리스트(즉 연결된 노드들 리스트 배열) forEach 전부
if(!visited[neighbor]){ // 방문사실이 없다면, 즉 아직 간 노드가 아니라면
return dfs(neighbor) //재귀적으로 헬퍼 함수에 넣는다
}
});
})(start); // ()()이렇게 해주는건 함수 선언하고 바로 start를 첫번째 입력값으로 하는것
return result;
}
// A
// / \
// B C
// | |
// D --- E
// \ /
// F
//
{
"A" : ["B", "C"],
"B" : ["A", "D"],
"C" : ["A", "E"],
"D" : ["B", "E", "F"],
"E" : ["C", "D", "F"],
"F" : ["D", "E"]
}
g.depthFirstRecursive("A")
-> [ "A", "B", "D", "E", "C", "F"]먼저 A가 헬퍼함수에 들어가고 visited에 “A”: true가 생김.
그리고 인접리스트에 B와 C가 forEach로 들어가는데 먼저 B가 다시 헬퍼 함수에 들어감.
콜스택에 쌓이는 모습 A→B→D→E→C→F 순서로 순회하는데 C가 막다른 길이다
C가 헬퍼함수에 들어갔을때 이미 인접리스트에 A와 E는 이미 방문했음.
그러면 여기서부터 쌓인 콜스택이 사라진다
반복적 용법의 DFS 그래프 순회
재귀를 사용하지 않고 그냥 스택을 사용한다
depthFirstIterative(start){
const stack = [start]; // 스택. 시작 노드가 들어가 있다
const result = []; // 결과를 담을 리스트
const visited = {}; // 방문했는지 기록
let currentVertex; // 현재 정점 변수를 선언한다
visited[start] = true; // 먼저 시작 노드를 방문했다고 기록
while(stack.length){ // 스택이 비어있지 않다면 계속 루프
currentVertex = stack.pop(); //스택 맨 뒤에 요소를 빼서 현재 변수로 지정
result.push(currentVertex); // 결과 리스트에 넣는다
this.adjacencyList[currentVertex].forEach(neighbor => { // 연결리스트에서 현재 정점을 키로 하는 배열, 즉 연결된 정점들을
if(!visited[neighbor]){ // 아직 방문하지 않았다면
visited[neighbor] = true; // 방문했다고 바꾸고
stack.push(neighbor) // 스택에 넣음
}
});
}
return result;
}
// A
// / \
// B C
// | |
// D --- E
// \ /
// F
//
{
"A" : ["B", "C"],
"B" : ["A", "D"],
"C" : ["A", "E"],
"D" : ["B", "E", "F"],
"E" : ["C", "D", "F"],
"F" : ["D", "E"]
}
-> [ "A", "C", "E", "F", "D", "B"]스택이 변하는 순서
[A] → [] → [B,C] → [B] → [B,E] → [B] → [B,D,F] → [B,D] → [B] → []
스택에 들어갔다가 사라지면서 결과 리스트에 들어간다. 그래서 재귀형과 받는 순서가 좀 다르다
재귀형에서는 인접리스트 앞에 있는 것부터 방문하고, 반복형에서는 인접리스트에 뒷쪽부터 먼저간다
BFS(너비 우선) 그래프 순회
너비 우선 방식은 주어진 노드의 모든 인접점을 방문한 다음에 아래로 내려가거나, 인접점의 인접점을 보게 되는 것이다.
스택 대신에 큐를 사용한다
