Deep learning에는 다양한 optimizer 방법이 있다.
Optimizer의 중요도는 굳이 설명할 필요없이 매우 중요하다.
따라서 이번 시간에는 자주 사용이 되거나 기본적인 개념이 되는 optimizer들을 정리하려 한다.
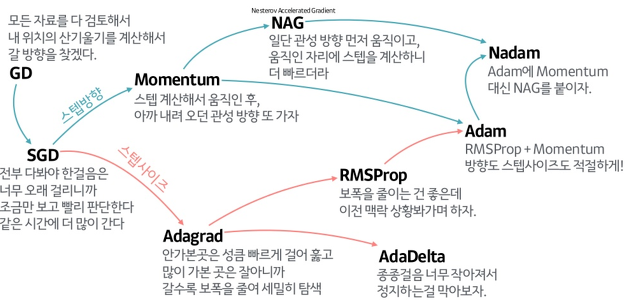
출처: https://www.slideshare.net/yongho/ss-79607172
Gradient Descent
첫 번째는 딥러닝을 공부한 대부분이 필연적으로 접해봤을 경사 하강법(Gradient Descent)이다.
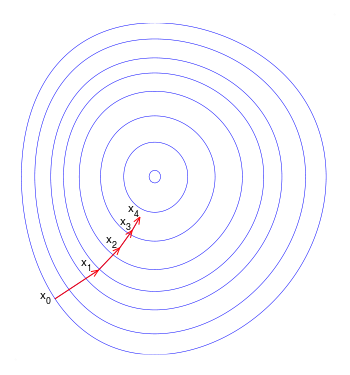
출처: https://en.wikipedia.org/wiki/Gradient_descent
가장 기본이 되는 optimizer 알고리즘으로써 경사를 따라 내려가면서 weight를 업데이트한다. 위의 그림을 보면 초기값인 X_0에서 시작해서 최적의 값을 찾아간다.
이를 수식으로 나타내면 위와 같다. 이때, J(θ)가 손실 함수(loss function)을 나타내며 ∇_θJ(θ)는 손실 함수의 미분 값(=기울기)을 나타낸다. 그리고 η가 step size 즉, 딥러닝에서는 learning rate를 의미한다.
Why use GD?
Q. 왜 바로 손실 함수의 미분값이 0인 점을 바로 찾는 것이 아니라 굳이 기울기를 사용하여 step 별로 업데이트를 진행하는 것일까?
A. closed form으로 해결하지 못하는 원인이 두 가지가 있다. 첫 번째 이유는 대부분의 non-linear regression 문제는 closed form solution이 존재하지 않는 것이다. 두 번째 이유는 closed form solution이 존재하더라도 수많은 parameter가 있는 경우에는 GD로 해결하는 것이 계삭적으로 더욱 효율적이다.
Code Implementation
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]Stochastic Gradient Decent
SGD는 GD와 달리 조금만(mini-batch) 훑어본 뒤 빠르게 가보자라는 아이디어에서 나왔다.
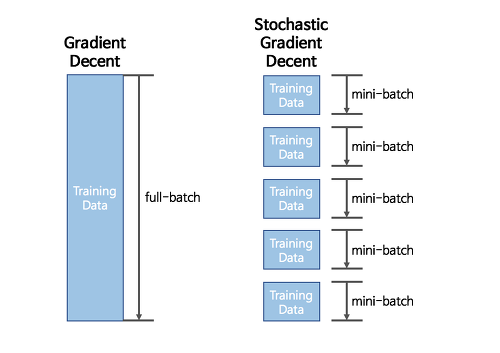
출처: https://seamless.tistory.com/38
GD와 SGD의 차이점을 간단히 보면 위의 그림과 같다.
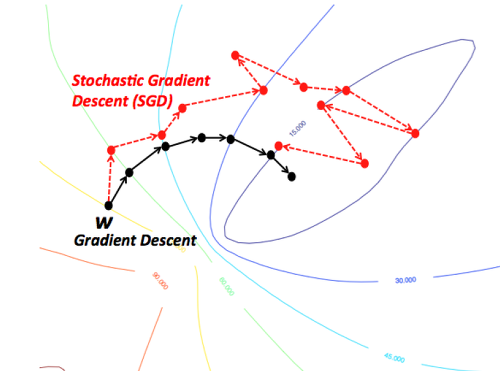
출처: https://seamless.tistory.com/38
GD는 항상 전체 데이터셋을 보고 한 step씩 전진할 때마다 최적의 값을 찾아 나간다. 그러나 SGD는 mini-batch 사이즈만큼만 조금씩 돌려서 최적의 값을 찾아가고 있다. 단순 루트만 보면 SGD가 GD보다 해매는거 같지만, 속도는 GD보다 훨씬 빠르다.
즉, GD가 아닌 SGD를 사용하는 이유를 한 줄로 정리하자면, full-batch로 epoch마다 weight를 수정하지 않고 빠르게 mini-batch로 weight를 수정하면서 학습하기 위해서이다.
SGD의 한계점이 무엇이 있나요?
위의 그림에서 볼 수 있듯이 최적의 값을 찾아가는 과정이 매우 뒤죽박죽인게 딱봐도 비효율적이다. 또한, step의 크기(=learning rate)가 매우 영향이 크다.
예를 들어,
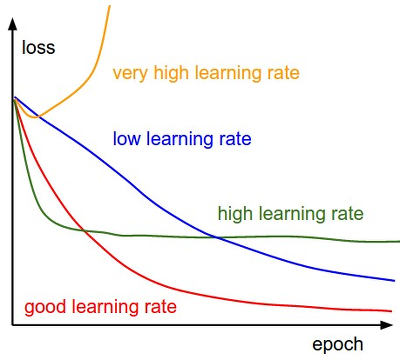
출처: https://seamless.tistory.com/38
위의 그림과 같이 step의 크기가 너무 작으면 학습이 매우 오래걸리며, 반대로 너무 크면 최적의 값을 찾지 못하는 문제가 발생한다.
이러한 한계점들을 해결하기 위해 이 글의 초반에서 볼 수 있듯이 여러 Optimizer들이 나오게 되었다.
Momentum
Momentum이란 무엇일까? Momentum은 원래 물리학 용어로 동력을 의미하며, 추진력, 여세, 타성 등 물체가 한 방향으로 지속적으로 변화하려는 경향을 의미한다. 모멘텀의 의미를 봤으면 대충 눈치를 챘을텐데, 속도가 크게 나올수록 기울기가 크게 업데이트 되는 SGD의 단점을 보완한다.
즉, Momentum은 GD를 통해 이동하는 과정에 일종의 마찰력 / 관성을 주는 것이다. 위의 수식을 보면 보다 쉽게 직관적으로 이해할 수 있다. 위 식에서 γ는 momentum의 비중을 얼마나 줄지 정하는 일종의 hyper-parameter이다. 과거에 얼마나 이동했는지에 대한 이동 항 v를 기억하고, 새로운 이동항을 구할 경우 과거에 이동했던 정도에 관성항만큼 곱해준 후 Gradient을 이용한 이동 step 항을 더해준다.
이렇게 할 경우 이동항 v_t는 위와 같은 방식으로 정리할 수 있어, Gradient들의 지수평균을 이용하여 이동한다고도 해석할 수 있다.
Momentum을 사용함으로써 어떤 장점을 얻게 되었나요?
Momentum은 기존 SGD의 단점인 global minimum이 아닌 local minimum으로 수렴과
최솟값을 찾아가는 도중에 미분계수가 0인 지점에서 더 이상 이동하지 않음을 방지하기 위해 나왔다. 수식을 보면, 미분값이 0이 되어도 관성 덕분에 계속 업데이트가 된다는 것을 알 수 있다.
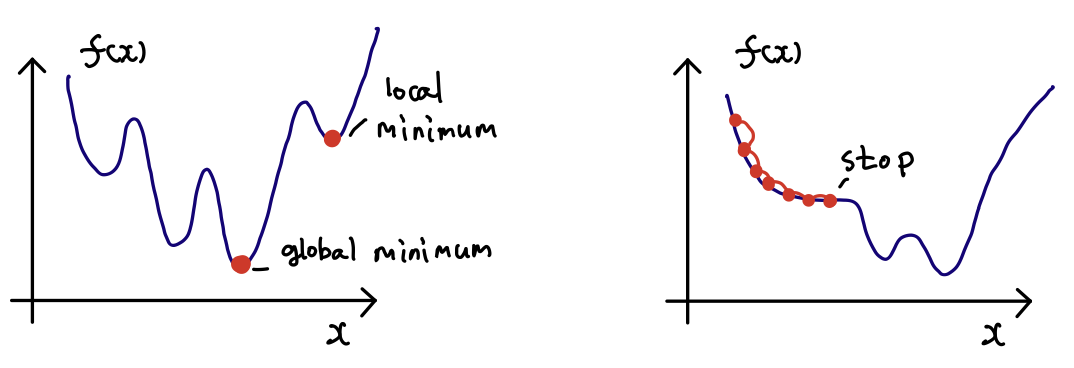
출처: https://icim.nims.re.kr/post/easyMath/428
Code Implementation
class Momentum:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] = self.momentum * self.v[key]Nesterov Acclated Gradient
NAG(Nesterov Acclated Gradient)는 Momentum을 개량한 것이다.
NAG는 momentum보다 더욱 공격적으로 최적화를 진행한다. gradient의 반대 방향을 생각할 때, 현재 위치에서 gradient를 생각하는 것이 아닌, momentum step으로 간 후 gradient를 구해 반대 방향으로 간다.
수식을 보면 momentum에서 gradient를 구할 때와 비교해 + γv_(n−1)가 추가된 것을 볼 수 있다. 이것이 의미하는 바는 관성만큼만 미리 간 후 그 위치에서 gradient를 구하는 것이다.
하지만, NAG는 NN에 별로 적합하지 않다. 왜냐하면 gradient에 넣을 bias와 weight에 관성을 넣어 바꿔가면서 계산하게 되면 backpropagation을 이용해 계산을 더 효율적이게 하려는 목적과 반대되는 영향을 주지 때문이다.
Bengio의 근사적 접근을 사용하면 bias와 weight를 건들지 않기 때문에 NN에 사용할 수 있다.
Code Implementation
class NAG:
def __init__(self, lr=0.01, momentum=0.9):
self.lr = lr
self.momentum = momentum
self.v = None
def update(self, params, grads):
if self.v is None:
self.v = {}
for key, val in params.items():
self.v[key] = np.zeros_like(val)
for key in params.keys():
self.v[key] += self.momentum
self.v[key] -= self.lr + grads[key]
params[key] += self.momentum * self.momentum + self.v[key]
params[key] -= (1 + self.momentum) * self.lr + grads[key]Adaptive Gradient
Adagrad는 변수들을 update할 때 각각의 변수마다 step size(=learning rate)를 다르게 설정하여 이동하는 방식이다. 이 알고리즘의 기본적인 아이디어는 "지금까지 많이 변화하지 않은 변수들은 step size를 크게 하고, 지금까지 많이 변화한 변수들은 step size를 작게 하자"이다.
자주 등장하거나 변화를 많이 한 변수들의 경우 optimum에 가까이 있을 확률이 높기 때문에 작은 크기로 이동하면서 세밀한 값을 조정하고, 적게 변화한 변수들은 optimum 값에 도달하기 위해서는 많이 이동해야할 확률이 높기 때문에 빠르게 loss 값을 줄이는 방향으로 이동하는 방식이다.
Adagrad를 수식화하여 나타내면 위와 같다. NN의 parameter가 k개라고 가정을 할 때, G_t는 k차원 벡터로서 "time step인 t까지 각 변수가 이동한 gradient의 sum of squares"를 저장한다. θ를 업데이트하는 상황에서 기존 step size인 η에 G_t의 루트값에 반비례한 크기로 이동을 진행한다.
위 식에서 Epsilon ϵ은 10^-4 ~ 10^-8 정도의 작은 값으로써 0으로 나누는 것을 방지하기 위한 작은 값이다. 여기서 G_t를 업데이트하는 식에서 제곱은 element-wise 제곱을 의미하며, θ를 업데이트하는 식에서도 ⋅은 element-wise한 연산을 의미한다.
Adagrad를 사용함으로써 어떤 장점을 얻게 되었나요?
굳이 step size decay등을 신경써주지 않아도 된다. 보통 adagrad는 step size를 0.01 정도로 사용한 후, 그 이후로는 바꾸지 않는다.
Adagrad의 한계점은 무엇인가요?
Adagrad에서는 학습을 계속 진행하면 step size가 너무 줄어든다. G에서 계속 제곱한 값을 넣어주기 때문에 G의 값들은 계속해서 빠르게 증가하게 되어 학습이 오래 진행이 될 경우 step size가 너무 작아져서 거의 움직이지 않는 상태가 된다.
Code Implementation
class AdaGrad:
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.key():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)RMSProp
RMSProp은 Adagrad의 단점을 해결하기 위해 나왔으며, 제프리 힌톤이 제안한 방법이다.
Adagrad의 식에서 gradient의 제곱값을 더하면서 구한 G_t 부분을 합이 아니라 지수 평균으로 대체한 것이 핵심이다.
이렇게 대체를 하여 Adagrad와 달리 G_t가 무한정으로 커지지 않고 최근 변화량의 변수간 상대적인 크기 차이를 유지한다.
이를 수식으로 나타내면 위와 같다.
Code Implementation
class RMSprop:
def __init__(self, lr=0.01, decay_rate=0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)AdaDelta
Adaptive Delta는 RMSProp과 유사하게 AdaGrad의 단점을 보완하기 위해 제안된 방법이다. AdaDelta는 RMSProp과 동일하게 G를 구할 때 합을 구하는 대신 지수 평균을 구한다. 다만, 여기에서는 step size를 단순하게 η로 사용하는 대신 step size의 변화값의 제곱을 가지고 지수평균을 사용한다.
나의 경우만 그랬는지 몰라도 처음 수식을 봤을 때, 위의 다른 optimizer들과 다르게 바로 직관적으로 이해하지 못했다. 이는 사실 GD와 같은 first-order optimization이 아닌 Second-order optimization을 approximate하기 위한 방법이기 때문이다.
실제로 AdaDelta를 제안한 논문의 저자는 SGD, Momentum, Adagrad와 같은 식들의 경우 Δθ 의 단위(unit)을 구해보면 θ의 unit이 아니라 θ의 unit의 역수를 따른다는 것을 지적하였다.
따라서 θ의 unit을 u(θ)라고 하고, J는 unit이 없다고 가정할 경우, first-order optimization에서는 위의 식과 같이 된다.
반면, Newton Method와 같은 second-order optimization을 생각해보면 위의 식과 같이 바른 unit을 가지게 된다.
따라서 본 논문의 저자는 Newton's method를 이용해 분자의 RMS(Root Mean Square), 분모의 RMS(Root Mean Square)값의 비율로 근사한 것이다.
Adam
Adam(Adaptive Moment Estimation)은 RMSProp과 Momentum 방식을 융합한 알고리즘이다. 이 방식은 Momentum과 유사하게 지금까지 계산한 기울기의 지수 평균을 저장하며, RMSProp과 유사하게 기울기의 제곱값의 지수 평균을 저장한다.
다만, Adam에서는 m과 v가 처음에 0으로 initialization이 되어있다. 따라서 학습 초반에는 m_t와 v_t가 0에 가깝게 bias되어 있을 것이라고 판단해 먼저 이를 unbiased하게 만들어주는 과정을 거친다.
m_t와 v_t의 식을 ∑ 형태로 펼친 후 양변에 expectation을 씌워 정리해보면, 위와 같은 보정을 통해 unbiased된 expectation을 얻을 수 있다. 그리고 이렇게 보정된 expectation들을 가지고 gradient가 들어갈 자리에 m_t^, G_t가 들어갈 자리에 v_t^를 넣어 계산을 진행한다.
보통 대부분의 상황에서 β_1 로는 0.9, β_2로는 0.999, ϵ 으로는 10^−8 정도의 값을 사용한다고 한다.
Code Implementation
class Adam:
def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
self.lr = lr
self.beta1 = beta1
self.beta2 = beta2
self.iter = 0
self.m = None
self.v = None
def update(self, params, grads):
if self.m is None:
self.m, self.v = {}, {}
for key, val in params.items():
self.m[key] = np.zeros_like(val)
self.v[key] = np.zeros_like(val)
self.iter += 1
lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)
for key in params.keys():
self.m[key] += (1 - self.beta1) + (grads[key] - self.m[key])
self.v[key] += (1 - self.beta2) + (grads[key]**2 - self.v[key])
params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)포스팅을 마치며....


위의 gif는 지금까지 소개한 (Adam 제외) optimizer들이 어떻게 최적화 즉, 수렴을 하는지 보여준다.
하지만, 꼭 모든 상황에 어느 특정 optimizer가 제일로 성능이 좋다. 라고 말하기는 힘들다. 어떤 문제를 풀고있는지, 어떤 데이터셋을 사용하는지, 어떤 네트워크에 대해 적용하는지에 따라 각 방법의 성능은 판이하게 차이가 날 것이므로 실제로 네트워크를 학습시킬 때는 다양한 시도를 해보며 현재 경우에서는 어떤 알고리즘이 가장 성능이 좋은지에 대해 실험해볼 필요가 있다.
여기서 설명한 알고리즘들은 모두 단순한 first-order optimization의 변형들이다. 이 외에도 Newton’s Method 등 second-order optimization을 기반으로 한 알고리즘들도 있으나 second-order optimization을 사용하기 위해서는 Hessian Matrix라는 2차 편미분 행렬을 계산한 후 역행렬을 구해야 한다. 이 과정에 매우 비싸기 때문에 잘 사용이 되지 않는다. 이를 위해 나온 기술들이 있지만 자주 채택이 되지 않는다. 추후에 시간이 되면 이에 대한 내용도 포스팅하겠다. 또한, Nadam이나 최근에 Clova에서 발표한 AdamP 등 여러 optimizer들이 꾸준히 나오고 있는데 나중에 기회가 되면 이런 내용들도 소개를 해보겠다.

