Greedy Algorithm

1. Greedy Algorithm 이란?

Greedy algorithm은 탐욕(적) 알고리즘 혹은 욕심쟁이 알고리즘이라고도 불리며, 여러 경우 중 하나를 결정해야 할 때마다 그 순간에 최적이라고 생각되는 것을 선택해 나가는 방식이다.

탐욕 알고리즘의 조건

탐욕 알고리즘을 효율적으로 활용할려면 탐욕스러운 선택 조건(greedy choice property)와 최적 부분 구조 조건(optimal substructure) 두 가지 속성을 만족해야한다.

전자는 선택이 이후 선택에 영향을 주지 않는 다는 것을 의미하고, 후자는 문제 전체에 대한 최적해(global optimum)가 부분 문제에 대해서도 역시 최적해가 된다는 것을 의미한다.

어떻게 활용이 되지?

예시를 몇가지 살펴보면서 어떻게 사용이 되는지 알아보겠다.

1. 분할 가능 배낭 문제(Fractional knapsack problem

한 광부가 최대 30g까지 넣을 수 있는 배낭이 있을 때, 일정 가치와 무게가 있는 광석들을 어떻게 배낭에 넣어야지 가치의 합이 최대가 되는지 방법을 찾아라.

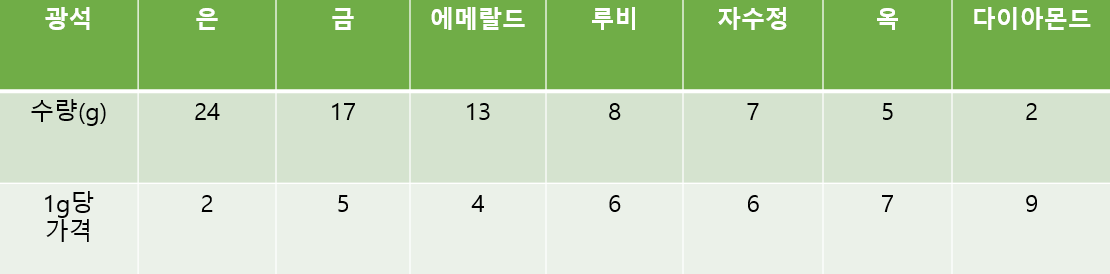
Greedy algorithm은 먼저 가장 값어치가 높은 아이템을 채워야 한다. 위와 같은 경우는 먼저 1g당 가격을 기준으로 내림차순 정렬을 한다. 그리고 배낭의 무게(=30g)을 초과하지 않을 때까지 비싼 순으로 채운다.

# W: 배낭의 무게, w: 각 광석의 무게, p: 각 광석의 가치
def knapsack(W, w, p):
    n = len(w) - 1
    k = [0] * (n + 1)
    weight = 0
    for i in range(1, n + 1):
        weight += w[i]
        k[i] = w[i]
        if (weight > W):
            k[i] -= (weight - W)
            break

    return k

또한, 탐욕 알고리즘은 교실 할당(Classroom assignment)이나 허프만 코딩(Huffman Coding) 등의 문제에 적용을 할 수 있다.