파보나치 수열 정의

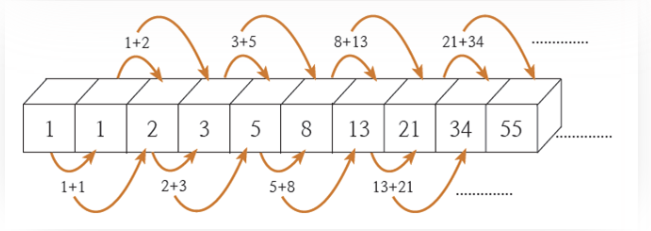
수학에서 파보나치 수(영어: Fibonacci numbers)는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다. 처음 여섯 항은 각각 1, 1, 2, 3, 5, 8이다. 편의상 0번째 항을 0으로 두기도 한다.

점화식: F{n}=F{n-1}+F{n-2}

⏩ 파보나치 수 F{n}는 다음과 같은 초기값 및 점화식으로 정의되는 수열이다.

⁂ 다음 정의에 따라 파보나치 수열을 16번째 항까지 나열해 보면 다음과 같다.

• (0), 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987

📗 파보나치 수열은 음수에서도 활용이 가능하다.

algorithm

파보나치 수열의 n번째 항을 구하는 알고리즘은 반복과 재귀 두 가지 형식으로 구현할 수 있다.

• 반복

 public int fibonacci (int n) {

    if (n <= 1) return n; // n이 1보다 작을 때는 해당 값을 그대로 반환한다.
    else {

        int result = 0;
        int iterA = 0, iterB = 1;

        for (int i = 2; i <= n; i++) {

            result = iterA + iterB;
            iterA = iterB;
            iterB = result;

        } // n항의 값을 구한다.

        return result;

    }
	
}

• 재귀

  public int fibonacci(int n) {
      int result = 0;
      
     if (n <= 1) return n; // n이 1보다 작을 때는 해당 값을 그대로 반환한다.
     if(num == 1) {
  			result = 1;
  	} else if (num == 2) {
  			result = 1;
  	} else if (num >= 3) {			
  			result = fibonacci(num -2) + fibonacci(num - 1);
  	}
  		
  	return result;
  }

분할 정복을 이용한 알고리즘.

분할 정복의 정의

예시

동작 방식

파보나치 수열 알고리즘 코드

• 정의
  문제를 직접 해결할 수 있을 만큼 간단해질 때까지 동일하거나 관련된 유형의 두 개 이상의 하위 문제로 재귀적으로 분해.
  ⏭ 큰 문제를 작은 문제로 분할하여 각각 해결한 다음, 그 결과를 합쳐서 전체 문제를 해결하는 알고리즘 설계 기법
  
• 예시

1. 병합 정렬(Merge Sort)
2. 퀵 정렬(Quick Sort)
3. 이진 검색(Binary Search)

• 동작 방식

1. 분할(Divide): 주어진 문제를 작은 사이즈의 부분 문제로 분할되며, 분할된 문제는 각각 독립적으로 해결 -> 주로 재귀 함수 사용.

2. 정복(Conquer): 작은 문제를 각각 재귀적으로 해결

3. 합병(Merge): 작은 문제의 해를 합병하여 전체 문제의 해를 구함.

• 코드

// 파보나치 수열을 구하는 함수를 작성
public static long[] fibonacci(int n) {
    if (n == 0) return new long[]{0};
    if (n == 1) return new long[]{0, 1};

    long[][] matrix = {{0, 1}, {1, 1}};
    long[][] result = pow(matrix, n - 1);

    long[] fibonacci = new long[n];
    fibonacci[0] = 0;
    fibonacci[1] = 1;
    for (int i = 2; i < n; i++) {
        fibonacci[i] = result[0][1] * fibonacci[i-1] + result[1][1] * fibonacci[i-2];
    }

    return fibonacci;
}

// 행렬의 거듭제곱을 구하는 함수
public static long[][] pow(long[][] matrix, int n) {
    if (n == 0) return new long[][]{{1, 0}, {0, 1}};

    long[][] half = pow(matrix, n/2);
    long[][] result = multiply(half, half);

    if (n % 2 == 1) {
        result = multiply(result, matrix);
    }

    return result;
}

//  행렬의 곱셈을 구하는 함수
public static long[][] multiply(long[][] a, long[][] b) {
    long[][] c = new long[2][2];
    for (int i = 0; i < 2; i++) {
        for (int j = 0; j < 2; j++) {
            for (int k = 0; k < 2; k++) {
                c[i][j] += a[i][k] * b[k][j];
            }
        }
    }
    return c;
}

출처
https://namu.wiki/w/%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98%20%EC%88%98%EC%97%B4#toc
https://velog.io/@pjj186/JAVA-%EC%9E%AC%EA%B7%80-%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0
https://namu.wiki/w/%ED%94%BC%EB%B3%B4%EB%82%98%EC%B9%98%20%EC%88%98%EC%97%B4#s-8.1