• 출제진: vkdldjvkdnj
• 검수진: ibm2006, iktk, measurezero, mujigae, ufshg, utilforever, w8385

검수진 분들과 대회 플랫폼을 지원해 주신 startlink께 다시 한 번 감사드립니다!

• 수정 내역

1. 2023.12.30 1차 수정 (시간 복잡도 추가, C번 풀이 추가, 일부 문장 수정 및 추가)

A. 진주로 가자! (Easy)

• Implementation (Easy)
• 제출 318번, 정답 201명 (정답률 65.723%)
• 처음 푼 사람: patata22, 1분
• 출제자: vkdldjvdnj
• 시간 복잡도: $O(N)$

  $N$개의 교통편 중에서 jinju가 목적지인 교통편의 요금 $C_j$를 찾고, $C_j$보다 비싼 교통편의 개수를 세는 문제입니다.

  모든 교통편의 정보를 tuple의 형태로 하나의 배열에 전부 담아봅시다. 그리고 그 중에서 목적지가 jinju인 교통편을 먼저 찾아봅니다. 찾았으면 그 교통편의 요금을 변수 $C_j$에 저장합니다.

  이제 다시 모든 교통편을 훑으면서, $C_j$보다 비싼 교통편의 개수를 세어봅니다. 그러면 결국 문제가 원하는 두 정답을 얻게 됩니다. 간단한 문제입니다.

B. 진주로 가자! (Hard)

• Implementation (Easy)
• 제출 563번, 정답 99명 (정답률 21.847%)
• 처음 푼 사람: p_ce1052, 4분
• 출제자: vkdldjvdnj
• 시간 복잡도: $O(N)$

  Easy 문제와 제한만 다른 동일한 문제입니다.

  단순하게 먼저 떠올릴 수 있는 풀이는 모든 요금을 담은 배열을 정렬하고 $C_j$의 인덱스를 찾는 방법입니다. 하지만 이 방법은 공간 복잡도가 $O(N)$이 되므로 메모리 제한인 16MB을 넘어서게 되고 MLE가 납니다. 다른 방법을 찾아봅시다.

  모든 교통편의 요금 $C_i$의 범위는 $[1, 10^{15}]$이며, $C_j$의 범위는 $[1, 1\,000]$입니다. 그러면 요금이 $1\,000$ 초과인 교통편은 무조건 $C_j$보다 비싼 교통편이 됩니다.

  요금이 $1$ 이상 $1\,000$ 이하인 교통편들의 요금별로 개수를 저장할 수 있는, 크기 1,000(1-based index일 경우 1,001)인 배열과 같은 자료구조를 하나 만들어봅시다. $N$개의 교통편을 하나씩 입력받으면서 $1\,000$ 초과인 교통편은 따로 개수로 세어주고, 나머지는 만들어 놓은 자료구조에서 요금과 동일한 인덱스의 원소를 1 증가 시킵니다. 물론, jinju가 목적지인 교통편의 요금 $C_j$는 따로 저장해야 합니다.

  $N$개의 교통편을 모두 입력받고 위와 같이 처리했다면, 요금이 $C_j$ 초과 $1\,000$ 이하인 교통편의 개수는 자료구조에 저장되어 있고, 요금이 $1\,000$ 초과인 교통편의 개수는 따로 세두었기 때문에 이 둘을 합하면 $C_j$보다 비싼 교통편의 개수를 구할 수 있습니다.

C. 선택의 기로

• Sorting (Easy)
• 제출 135번, 정답 110명 (정답률 86.667%)
• 처음 푼 사람: patata22, 5분
• 출제자: vkdldjvdnj
• 시간 복잡도: $O(N \log N)$

  간단한 정렬 문제입니다.

  일단, 각 촉석루 미니어처의 품질과 가격을 묶어서 정렬이 가능한 자료구조에 저장합니다. 그리고 각 방법을 살펴봅시다.

  첫 번째 방법은 품질이 우선이며 가격이 차선입니다. 그러므로 비교하는 방법을 품질이 높은 게 우선이며, 동일하다면 가격이 낮은 것을 선택하게끔 만들어서 정렬하고 첫 번째, 두 번째 원소를 선택하면 됩니다.

  두 번째 방법은 가격이 우선이며 품질이 차선입니다. 그러므로 비교하는 방법을 가격이 낮은 게 우선이며, 동일하다면 품질이 높은 것을 선택하게끔 만들어서 정렬하고 첫 번째, 두 번째 원소를 선택하면 됩니다.

  $N$이 최대 $100\,000$이라서 $O(N \log N)$정렬을 두 번 해도 무방합니다.

  시간 복잡도를 줄일 수 있는 다른 방법도 있습니다. 입력을 받을 때마다, 첫 번째, 두 번째 방법에서의 구하고자 하는 값을 갱신하는 방법입니다. 이는 시간 복잡도가 $O(N)$입니다. 하지만, 솔루션을 떠올리는 과정과 코드로 풀어내는 과정은 정렬을 사용하는 방법이 훨씬 간단하다고 생각이 들어서 정렬을 사용하는 방법이 정해라고 생각합니다. (물론, $O(N \log N)$ 정렬을 직접 구현하지 않는다는 가정하에 말씀드리는 것입니다.)

D. 육회비빔밥

• Backtracking, Bruteforcing (Easy)
• 제출 96번, 정답 39명 (정답률 40.625%)
• 처음 푼 사람: p_ce1052, 12분
• 출제자: vkdldjvdnj
• 시간 복잡도: $O(N!)$

  방문하는 순서에 따라 시식대의 인덱스를 나열한다고 생각해봅시다. 나올 수 있는 모든 경우의 수를 살펴보면 순열과 동일함을 알 수 있습니다. $N$은 최대 $10$이므로 순열의 최대 경우의 수는 $10!$입니다. 그래서 모든 순열을 검사해도 무방한 시간 복잡도가 됩니다. 이는 백트래킹을 이용하면 되지만, 순열을 만들어 주는 함수를 사용하여 모든 순열에 대해 검사해도 무방합니다.

  하나의 순열을 검사할 때, 현재 검사하고자 하는 인덱스가 $i$이며 순열의 $i$번째 시식대의 번호가 $j$이고 순열의 $i-1$번째 시식대의 번호가 $k$이라면, $C_j \times C_k$가 $K$를 넘지 않아야 합니다. 이를 첫 번째 인덱스를 제외한 모든 인덱스에 대해 검사를 하고 충족한다면, $\sum_{i=2}^{N} (A_{i-1} \times B_i)$를 구해 정답을 갱신하면 됩니다.

E. 닭강정의 전설

• Prefix Sum (Easy)
• 제출 40번, 정답 31명 (정답률 77.500%)
• 처음 푼 사람: p_ce1052, 18분
• 출제자: vkdldjvdnj
• 시간 복잡도: $O(N^2 + Q)$

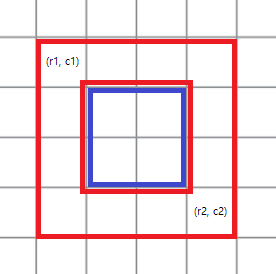
  $\sum_{i={r_1}}^{r_2} \sum_{j={c_1}}^{c_2} \left(k_{i,j} \times \begin{cases} 1 & \text{if } r_1 < i < r_2 \text{ and } c_1 < j < c_2 \\ -1 & \text{otherwise} \end{cases}\right)$ 이 식은 결국 두 점 $(r_1, c_1)$, $(r_2, c_2)$으로 이루어지는 직사각형에서 바깥쪽 테두리는 음의 가중치, 바깥쪽 테두리를 제외한 안쪽은 양의 가중치로 갖는 모든 칸의 합이라는 말입니다.

  

  일단은 특정 범위 내의 가중치 합을 구하는 방법을 생각해봅시다. 쿼리마다 범위로 주어지는 직사각형의 한 변에 포함되는 칸의 개수의 최대는 $5\,000$입니다. 그리고 쿼리는 최대 $100\,000$개가 들어올 수 있어서 Naive하게 구하는 방법은 불가능합니다.

  임의의 수열이 주어지고 수열의 변화가 일어나지 않으며, 수열의 임의의 구간 내 원소들의 합을 $O(1)$에 구하는 누적 합이라는 방법이 있습니다. 이 문제는 값의 변화가 일어나는 쿼리가 주어지지 않기 때문에 누적 합 알고리즘을 사용하여 해결할 수 있습니다. 또한, 수열이 아닌 행렬이 주어지므로 2차원 누적 합을 사용해야 합니다.

  바깥쪽 테두리는 빼야 하고, 안쪽은 더해야 하기 때문에 range_sum(r1, c1, r2, c2)를 $(r_1, c_1)$, $(r_2, c_2)$ 사이의 2차원 구간 합을 구하는 함수라고 정의한다면, range_sum(r1 + 1, c1 + 1, r2 - 1, c2 - 1) * 2 - range_sum(r1, c1, r2, c2)로 값을 구하면 됩니다. 안쪽 구간합을 두 번 더하면 바깥쪽을 포함한 구간 합이 빠질 때 한 번 더 더했던 안쪽 구간합이 같이 빠지기 때문입니다.

  참고로 1차원 누적 합을 사용하는 방법은 TLE입니다.

F. Shoot! Take a Panorama

• Math, Statistics, Ternary Search (Medium)
• 제출 37번, 정답 11명 (정답률 29.730%)
• 처음 푼 사람: kimjihoon, 35분
• 출제자: vkdldjvdnj
• 시간 복잡도: $O(N (\log X_{range} + \log Y_{range}))$ or $O(N)$

  

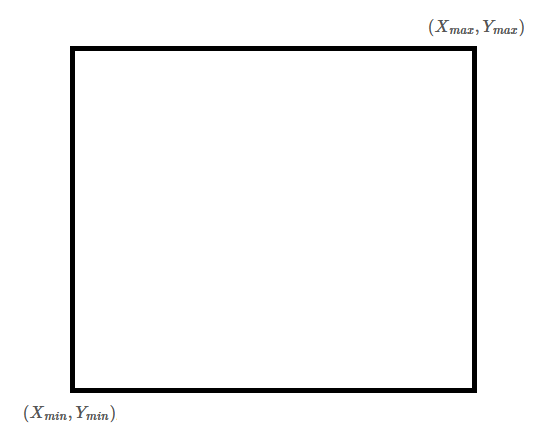
  빛나무원은 이런 직사각형 모양의 공간입니다. 우리가 찾고자 하는 파노라마 포토 스팟은 빛나무원의 경계나 안에는 있을 수 없습니다.

  사진의 불만족도는 (빛나무와의 유클리드 거리의 제곱) $\times$ (빛나무의 밝기)의 합입니다. 이는 당연히 빛나무와의 유클리드 거리가 멀어질수록 커집니다. 그래서 파노라마 포토 스팟은 빛나무들과 최대한 가까울 수 있는 빛나무원의 네 변과의 거리가 1인 곳 중 하나가 됩니다.

  이제 네 변을 따라 훑기만 하면 되는데, 가능한 모든 좌표를 검사하기엔 제한이 너무 큽니다. 자, 이제 여기서 풀이가 크게 두 개로 나뉩니다.
  
  

  • 삼분 탐색 (문제 출제할 때 정해로 잡았던 방법)

  이 문제는 사실 저의 Guess That Car! 삼분 탐색 풀이에서 모티브를 얻었습니다. 이 풀이도 같이 참고하시면 좋을 듯 합니다.

  $\sum_{i=1}^{N} \left(\left(\left(X_c - X_i\right)^2 + \left(Y_c - Y_i\right)^2\right) \times L_i\right) = \sum_{i=1}^{N} \left(\left(X_c - X_i\right)^2 \times L_i\right) + \sum_{i=1}^{N} \left(\left(Y_c - Y_i\right)^2 \times L_i\right)$로 전개할 수 있습니다. 결국 $X_c$와 $Y_c$에 대한 값은 독립적이란 것을 알 수 있습니다.

  지금 우리는 네 변을 따라 훑어야 합니다. 즉, $X_c$에 대한 값은 $[X_{min}, X_{max}]$ 범위로 하여금 각 $(X_c, Y_{min}-1)$, $(X_c, Y_{max}+1)$에 대한 값을 찾아야 하고, $Y_c$에 대한 값은 $[Y_{min}, Y_{max}]$ 범위로 하여금 각 $(X_{min}-1, Y_c)$, $(X_{max}+1, Y_v)$에 대한 값을 찾아야 합니다.

  식은 이차함수 꼴이므로 아래로 볼록한 그래프 모양입니다. 그래서 위에서 서술한 네 방법을 삼분 탐색으로 값을 찾으면 됩니다.
  
  

  • 회귀분석 (검수진 분들이 찾은 방법)

  수직선 상에서 잔차제곱이 최소가 되는 점은 좌표들의 평균점이라고 합니다. 밝기가 $K$인 점은 그 자리에 밝기가 $1$인 점이 $K$개 있는 것과 동치라는 점을 이용하여, $K$를 가중치로 하여금 평균점을 구합니다. 엄밀하게는 $X$의 평균과, $Y$의 평균을 구해야 합니다.

  이제 후보는 네 점 $(X_{avg}, Y_{min}-1)$, $(X_{avg}, Y_{max}+1)$, $(X_{min}-1, Y_{avg})$, $(X_{min}-1, Y_{avg})$으로 좁힐 수 있습니다. 이유는 첫 번째 방법에서 서술한 식 전개 시 $X_c$와 $Y_c$의 값은 독립적임을 알 수 있기 때문입니다.

  그런데 문제가 있습니다. 파노라마 포토 스팟이 될 수 있는 좌표는 무조건 정수로 이루어진 좌표이어야 합니다. 그래서 위에서 구한 평균값을 정수로 나타낸 뒤, 오차를 고려하여 $±1$을 해서도 살펴보아야 합니다.

  그리고 이 풀이에서 주의해야 할 Edge Case가 있습니다. 바로, 모든 빛나무의 밝기가 0인 TC가 있습니다. 모든 빛나무의 밝기가 $0$일 경우엔 평균점을 구할 수 없으므로, 따로 처리를 해야 합니다.

G. What's your ETA?

• Dijkstra, Sieve (Medium)
• 제출 68번, 정답 21명 (정답률 36.765%)
• 처음 푼 사람: p_ce1052, 25분
• 출제자: vkdldjvdnj
• 시간 복잡도: $O(D_{max} \log \log D_{max} + M \log N)$

  문제에서 원하는 것은 쉽게 알 수 있습니다.

  • 현재 정류장의 재난 코드와 가고자 하는 정류장의 재난 코드의 합이 소수인가?
  • $1$번에서 $N$번으로 가는 최단 거리(시간)

  첫 번째부터 살펴봅시다.
  모든 정류장의 재난 코드의 범위는 $[1,5\,000\,000]$입니다. 그러면 두 재난 코드의 합의 범위는 $[2,10\,000\,000]$입니다. 이는 충분히 에라토스테네스의 체으로 소수 판정이 가능한 범위입니다. 그리고 소수 판정이 쓰이는 간선이 최대 $1,000,000$이므로 소수 판정이 필요할 때마다 하는 방법 $O(\log D)$는 이론적으로 가능해보일 수 있으나, 이 문제 자체의 시간 복잡도 상수가 꽤 커서 아슬아슬하게 막아놓았습니다. (에라토스테네스의 체를 사용하지 않고 뚫은 검수진 분도 계셨습니다.)

  이제 소수 판정이 가능해져서 버스 정류장 사이의 도로가 이용이 가능한 지 판별이 가능해졌습니다. 그럼 두 번째를 살펴봅시다.
  간선의 가중치가 서로 다른 그래프에서의 최단 거리를 구하는 방법은 플로이드-워셜이나 SPFA 그리고 다익스트라가 있습니다. 하지만 $O(N^3)$이나 $O(NM)$를 시간 복잡도로 갖는 플로이드-워셜이나 SPFA는 부적합합니다.

  이제 첫 번째와 두 번째를 어떻게 버무리냐면

  1. 에라토스테네스의 체로 소수 판정 배열을 만들었다면 처음에 주어지는 간선이 가능한 간선으로만 전처리 후 다익스트라
  2. 에라토스테네스의 체로 소수 판정 배열을 만들고 다익스트라를 돌릴 때 우선순위 큐에 넣는 조건에 거리뿐만 아니라 두 정류장의 재난 코드의 합이 소수이어야 하는 조건도 추가

  위 두 방법 중 하나를 택해 풀어내면 됩니다.

H. 약간 모자라지만 착한 친구야

• Tsp (Medium)
• 제출 28번, 정답 9명 (정답률 32.143%)
• 처음 푼 사람: p_ce1052, 45분
• 출제자: vkdldjvdnj
• 시간 복잡도: $O(N^22^N)$

  모든 곳을 한 번씩만 방문하고 출발지로 돌아오는 문제는 해밀턴 순환 문제입니다. 그리고 그 중에서 비용의 최솟값을 찾는 문제는 외판원 순회 문제이며, 이 문제는 외판원 순회 문제에 해당합니다. 그리고 경상국립대를 포함한 $N$이 최대 15이기 때문에 단순 백트래킹($O(N!)$)으로 풀리지 않습니다. 이는 Bit DP를 이용하여 풀어내면 됩니다. 물론, 다른 방법도 있지만 가장 쉬우면서도 널리 알려져 있는 Bit DP로 설명하겠습니다. 여기까지는 이 문제와 전혀 다를 것이 없습니다.

  하지만 이 문제에는 하나의 제약이 있습니다. 일부 지점에 방문하기 위한 조건은 그 지점에 정해진 다른 지점의 방문 이력이 있어야 한다는 것입니다. 방문 이력이 있어야 하는 다른 지점을 이제부터 선행 지점이라고 칭하겠습니다.

  외판원 순회 문제에서 Bit DP의 비트필드는 비트가 켜져 있는 상태로 어떤 지점이 방문되어 있는 지를 나타냅니다. 예를 들면 01001과 같은 비트필드이면 $1 << 0$ | $1 << 3$인 비트와 동일하므로, 0,3번째(0-based index) 지점이 방문되었음을 나타냅니다. 그래서 비트필드로 각 지점의 선행 지점이 방문되었는지 알 수 있습니다. 그래서 비트필드가 어떤 지점의 선행 지점이 방문된 상태임을 나타낼 때, 그 어떤 지점으로 가보는 방식으로 Bit DP를 진행하면 됩니다. 이는 왜 정당성이 있는 걸까요?

  외판원 순회 문제에서 Bit DP의 점화식은 $TSP(now, visited) = min(TSP(now, visited), TSP(next, visited | (1 << next)) + distance[now][next])$입니다. 이를 말로 쉽게 풀어내면 다음과 같습니다.
  (현재 상태에서의 방문하지 않은 남은 지점들을 방문하는 최단 거리)는, 현재 지점에서 갈 수 있는 모든 다음 지점에서의 (다음 상태에서의 방문하지 않은 남은 지점들을 방문하는 최단 거리) + 현재 지점과 다음 지점의 거리의 최솟값이 되는 겁니다. 이는 지금까지 왔던 경로가 달라도 현재 지점과 앞으로 남은 지점이 같으면, 앞으로 남은 지점에 대한 경로에 대한 최솟값은 동일함을 이용하는 Bit DP입니다. 이는 곧 현재 지점과 현재 상태가 같으면, 지금까지 왔던 경로에 대한 값과 이제부터 가는 경로에 대한 값은 서로 영향을 주지 않는다는 말입니다. 이는 그리디적인 속성이라고 볼 수 있습니다.

  그러면 어떤 지점의 선행 지점이 방문되지 않아서 거기로 가지 않음을 선택하지 않는다고, Bit DP가 깨질까요? 아닙니다. 그냥 수많은 경로 중에서 일부 경로가 사라지는 것일 뿐입니다. 즉, $TSP(now, visited)$에 대해 $visited$을 이뤄온 일부 경로나 가능한 $next$가 일부 사라질 뿐입니다.

I. 사랑의 큐피드

• Bipartite Matching (Medium)
• 제출 26번, 정답 13명 (정답률 57.692%)
• 처음 푼 사람: jh01533, 14분
• 출제자: vkdldjvdnj
• 시간 복잡도: $O((N+M) \log E); E = \text{Number of Edges}$

  각 여학생과 각 남학생을 그래프 상의 정점이라고 생각해봅시다. 여학생은 다른 여학생과 이어질 수 없습니다. 또한, 남학생은 다른 남학생과 이어질 수 없습니다. '키'라는 조건하에 여학생은 일부 남학생과, 남학생은 일부 여학생과 이어질 수 있습니다. 이렇게 이어질 수 있는 관계를 간선으로 생각해봅시다.

  위에서 나타낸 그래프는 곧 이분 그래프입니다. 모든 간선의 양 끝점이 서로 다른 그룹에 속하며, 정점은 두 그룹으로 나눠지기 때문입니다. 이제 우리는 주어진 이분 그래프에서 최대한 많은 간선을 선택해야 합니다. 선택하는 간선은 곧 커플이기 때문입니다. 단, 모든 정점은 선택된 간선 중 하나의 간선에만 포함되어야 합니다. 이러한 문제는 곧 이분 매칭이라고 불리는 문제입니다.

J. 금강산도 식후경

• Exponentiation By Squaring, FFT, KMP (Hard)
• 제출 9번, 정답 3명 (정답률 33.333%)
• 처음 푼 사람: kimjihoon, 127분
• 출제자: vkdldjvdnj
• 시간 복잡도: $O(\max(T) M \log (\max(T)M) + \max(T) M + \max(D))$

  문제 지문을 보면 풀이 과정이 상당히 직선적입니다. 그대로 따라가봅시다.

  모든 재료의 개수는 무제한이며, 음식에 들어가는 재료의 종류는 상관이 없고 개수만 정확하게 M개이어야 합니다. 그리고 만들 수 있는 음식을 모두 만들며, 보선이의 식사 계획은 음식의 자극도에만 영향을 받습니다.

  재료 종류가 2개이며 자극도가 각각 1, 1이라고 생각해봅시다.
  $M = 1$이면, 만들어지는 음식의 자극도는 1(1번 재료), 1(2번 재료)입니다.
  $M = 2$이면, 만들어지는 음식의 자극도는 2(1번 재료 + 1번 재료), 2(1번 재료 + 2번 재료), 2(2번 재료 + 2번 재료)입니다.
  우리는 음식의 개수가 아닌 자극도의 개수를 구해야 합니다. 즉, 중복되는 값을 제외해야 합니다. 결국 두 경우에서 식사 계획 $D$를 신경쓰지 않고 $F_1$로 가능한 자극도의 개수는 하나씩입니다.

  $N$개의 값(재료의 자극도) 중에서 중복이 허용되게끔 $M$개를 선택하여 나올 수 있는 모든 값을 구해야 합니다. 뭔가 많이 본 유형의 문제 같지 않나요? 맞습니다. FFT 문제입니다.

  각 재료의 자극도는 최대 1,000입니다. 이 크기에 맞게 하나의 다항식을 만들어서 재료마다 (자극도)차항의 계수를 1로 만듭니다. 즉, 크기에 맞게 배열을 만들고 인덱스가 재료마다의 자극도인 곳을 1로 만들면 됩니다.
  그리고 만들어진 다항식(배열)을 사용하여 다항식(배열)$^M$을 만들어주면 됩니다.

  그런데 배열의 크기를 처음부터 최대로 잡는다는 가정하에 $O(\max(T) M \log (\max(T)M))$을 $M-1$번 연산을 해야 합니다. 너무 숨막히는 시간 복잡도입니다. 그래서 분할 정복을 이용한 거듭제곱을 이용하여 연산 횟수를 $log(M)$으로 줄여야 합니다. 이렇게 연산을 전부 종료하면, 만들어질 수 있는 모든 음식의 자극도마다 1 이상이 되어 있습니다. 즉, 다항식의 곱의 결과에서 계수가 1 이상인 모든 항의 차수가 만들어질 수 있는 모든 음식의 자극도입니다.

  자, 이제 만들어질 수 있는 모든 음식의 자극도를 중복없이 구했습니다. 이제 식사 계획 $D$를 살펴봐야 합니다. 지문을 잘 풀어서 생각해보면, $F_1$, $F_1 + D_2$, $F_1 + D_3$, $\dots$, $F_1 + D_K$는 모두 만들 수 있어야 하고, $[F_1, F_1 + D_K]$에 포함되면서 $F_1$, $F_1 + D_2$, $F_1 + D_3$, $\dots$, $F_1 + D_K$에 포함되지 않는 음식이 만들어지면 안된다는 것을 알 수 있습니다.

  이를 간단하게 예제 입력 1, 2로 설명해보겠습니다.
  자극도가 1, 3인 두 종류의 재료를 3번 사용하여 만들 수 있는 음식의 자극도는 3, 5, 7, 9가 있습니다. 이를 자극도 1부터 자극도 9까지 만들 수 있으면 '1', 없으면 '0'으로 표현하여 문자열 $S$로 만들면 '001010101'이 됩니다.

  예제 입력 1에서의 식사 계획 $D$를 위 방법과 동일하게 문자열 $T_1$으로 만들면 '101'이 됩니다. 자, 뭔가 감이 오시나요? $T_1$를 $S$에 매칭 가능한 경우의 수가 정답이 됩니다. $T_1$를 $S$에 매칭 가능한 경우의 수의 첫 인덱스는 각각 3, 5, 7이 됩니다. (1-based index)

  예제 입력 2에서의 식사 계획 $D$를 위 방법과 동일하게 문자열 $T_2$으로 만들면 '111'이 됩니다. $T_2$를 $S$에 매칭 가능한 경우의 수는 없으므로 정답은 0입니다.

  이는 문자열 매칭 알고리즘로 해결할 수 있습니다. 대표적인 알고리즘으로 KMP가 있습니다. 식사 계획 D를 나타낸 배열을 위에서 구한 FFT의 결과인 다항식에 매칭 가능한 경우의 수를 구하면 됩니다.

K. 버스 기사 집합지

• Bitmask, Segment Tree Beats (Hard)
• 제출 4번, 정답 1명 (정답율 25.000%)
• 처음 푼 사람: kimjihoon, 230분
• 출제자: vkdldjvdnj
• 시간 복잡도: $O(NK \log N); K = 51(\text{numbers of bit})$

  딱 봐도, 문제 지문 그대로 구간 내의 집합지에 버스 기사를 더하고 빼면 TLE가 날 것 같은 문제입니다.

  일단, 우수한 버스 기사 집합지과 저조한 버스 기사 집합지의 선정 조건을 살펴봅시다. 운전 실력이 50인 버스 기사부터 확인하는데, 버스 기사의 수가 영향을 주나요? 아닙니다. 0명인지 1명 이상인지가 중요합니다.
  또한, 출력 쿼리를 보면 모든 운전 실력을 중복을 제외하고 출력을 하라고 되어 있습니다.
  이러한 부분들에서 우리는 버스 기사 집합지에서 운전 실력마다 버스 기사의 수가 아닌 버스 기사가 있는지만 체크하면 된다는 점을 알 수 있습니다.

  이제 체크를 어떻게 할 것이냐가 관건입니다. 버스 기사의 운전 실력의 범위는 $[0, 50]$입니다. 충분히 비트마스킹으로 상태를 나타낼 수 있는 범위입니다.
  즉, 운전 실력이 0, 2, 3인 버스 기사가 있는 버스 기사 집합지의 상태는 0b1011 = 11가 되는 것입니다. 물론, 주어지는 변경 쿼리의 상태도 전부 비트마스킹으로 표현할 수 있음을 알 수 있습니다.

  자, 이제 각 버스 기사 집합지의 상태와 변경 쿼리의 상태를 모두 비트마스킹으로 나타낼 수 있으니, 주어지는 쿼리들을 어떻게 처리해야 할까요?

  1번 쿼리는 주어지는 운전 실력에 대한 비트가 켜집니다. 이는 or 쿼리와 동일합니다.
  2번 쿼리는 주어지는 운전 실력에 대한 비트를 제외한 모든 비트는 꺼집니다. 이는 and 쿼리와 동일합니다.
  5번 쿼리는 구간 $[A, B]$ 내의 min 쿼리와 동일합니다.
  6번 쿼리는 구간 $[A, B]$ 내의 max 쿼리와 동일합니다.

  이는 Segment Tree Beats(이하 세그비츠)의 유명한 문제 중 하나입니다. 세그비츠는 이제 꽤 웰논(?)이라고 할 수 있습니다. 간단하게 설명하면 lazyprop에서의 tag, break condition을 적절한 조건으로 교체해서 구간 쿼리 문제를 해결하는 알고리즘인데, Koosaga님 블로그와 JusticeHui님 블로그에 설명이 잘 되어 있으니 참고 및 공부는 저 두 블로그에서 하면 됩니다.

  이 문제에서는 or과 and가 각 구간에서 tag를 할 때, 쿼리와 같이 주어진 수의 켜져 있는 비트가 이 구간에 전혀 영향을 미치지 못하는지와 구간 내 모든 원소에 동일한 변경을 주는지에 대해서 확인 및 break, tag condition을 교체하면 됩니다.

  or과 and가 각각 구간 내 모든 원소에 동일한 변경을 주면, 이에 따라 그 구간의 min과 max는 동일한 변경을 받기 때문에, min과 max는 lazy 값을 push하면서 같이 업데이트해주면 됩니다.

  이제 남은 쿼리에 대해 설명해보겠습니다.

  3번 쿼리는 $A_i = x$ 쿼리입니다. 잘 읽어보면, 그 집합지에는 $L_1$, $\dots$, $L_M$을 운전 실력으로 갖춘 버스 기사만 남게 됩니다.
  4번 쿼리는 말 그대로 두 집합지의 상태가 교체됩니다.
  위 두 쿼리는 and와 or 쿼리를 적절하게 사용하여 처리가 가능합니다. $x∧0=0$과 $0∨x=x$를 이용하면 됩니다.

  7번 쿼리는 우수한 버스 기사 집합지에서 켜져 있는 비트 중 임의의 비트로 하여금 저조한 버스 기사 집합지에서 켜서 저조한 버스 기사 집합지을 우수한 버스 기사 집합지으로 만들 때의 필요한 비트의 최소 개수입니다. 이 쿼리는 함정 아닌 함정이 있습니다. 일단, 저조한 버스 기사 집합지의 켜진 비트를 $A$, 우수한 버스 기사 집합지의 켜진 비트를 $B$라고 하겠습니다. 그럼 단순히 $A\cap B^c$라고 생각할 수 있습니다만, 정답이 아닙니다.
  저조한 버스 기사 집합지의 켜진 비트 중 가장 높은 비트를 $b$라고 하겠습니다. 만약, $b$가 우수한 버스 기사 집합지에서 켜지지 않았다면 어떻게 될까요? $A\cap B^c$ 중에서 $b$보다 더 높은 비트들만 추가해도 저조한 버스 기사 집합지은 우수한 버스 기사 집합지가 됩니다. 이를 고려하여 풀어내면 됩니다.