백준 티어를 빠르게 올리고, 코드포스 대회도 다 참가하느라 요즘 좀 힘들다.
그래서 쉬엄쉬엄할 겸, solved.ac Class 문제를 차근차근 풀어보기 시작했다.
이 문제는 Class 5에 포함되어 있고 풀면서 약간 좀 감명받았다. 이유는 나중에 여담에 후술.
아무튼 감명받아서 풀이를 써볼까 한다.

BOJ 1007 - 벡터 매칭 링크
(2022.08.17 기준 난이도 G2)
(치팅말고 공부해요)

문제

N개의 점이 있고 각 점을 한 번만 사용하여 벡터 N/2개를 만드는 경우 중 벡터의 합의 최소값

알고리즘

먼저 모든 경우를 확인해야 한다. (브루트포스)
그리고 벡터의 합을 구하는 공식을 이용하여 브루트포스를 최적화해야 한다.

풀이

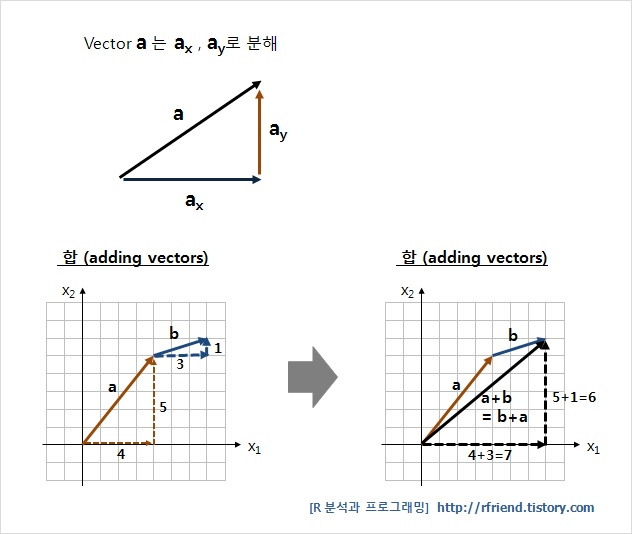
먼저 벡터의 합 공식을 살펴보자.

(이 링크의 블로그를 참고하였습니다)

위 그림처럼 벡터 a는 sqrt(ax ** 2 + ay ** 2)이다.
벡터 a + b는 sqrt((ax + bx) ** 2 + (ay + by) ** 2)이다.
그러면 벡터 a + b + c는 sqrt((ax + bx + cx) ** 2 + (ay + by + cy) ** 2)일 것이다.
결국 모든 벡터의 합은 sqrt(sum(x) ** 2 + sum(y) ** 2)가 된다.

하지만 위 그림은 (0, 0) -> (ax, ay) 기준이므로
만약 (a, b) -> (c, d)인 벡터이면 ((c - a) ** 2 + (d - b) ** 2)가 될 것이다.

이를 이용하여 정리하자면, 벡터의 합을 구할 때, 두 점이 벡터에 쓰이면 한 점은 좌표 값만큼 증가시키고 한 점은 좌표 값만큼 감소시킨다. (sum 값을 말이다.)

결국 N개의 점이 있으면 x, y의 합에다가 절반의 점들의 x, y의 합만큼 빼면
벡터의 시작 부분의 기준점이 될 것이고
좌표값의 합에 시작 부분의 기준점을 빼면 끝 부분의 기준점이 될 것이다.

그리고 이 과정을 모든 경우의 수에 적용하여 가장 작은 벡터 합을 구하면 된다.
python에선 combinations를 쓰자.

주의사항

위 풀이대로 그대로 코드로 옮겨 적으면, Python3는 시간 초과가 뜬다.

벡터 (a -> b)나 벡터 (b -> a)의 값은 같다. 벡터는 힘의 크기 그 자체를 나타내는 것이기 때문에 음수가 되지 않는다.

combinations 함수는 모든 경우의 수를 사전순으로 차례대로 반환해준다.

만약 1~10 까지의 수가 있고 5개를 뽑는 조합을 생각한다면 조합 수는 252개가 있다.
여기서 126개까지는 맨 앞이 1인 조합이 나오고 127번째는 맨 앞이 2인 조합 (2, 3, 4, 5, 6)이 나온다.
근데 이 조합은 전에 나온 조합인 (1, 7, 8, 9, 10)과 값이 동일하게 나올 것이다. 아까 서술했듯이 벡터에서 힘의 방향은 힘의 크기에 영향을 주지 않는다.
동일하게 뒤에 나오는 조합들도 다 전에 나왔던 값을 반환할 것이다.
그러므로 조합 수의 절반만 살펴보면 된다. (수학적 증명은 못하겠다. 난 수학자가 아니다..)

코드

import sys; input = sys.stdin.readline
from math import inf
from itertools import combinations
for _ in range(int(input())):
    N = int(input())
    pos = [list(map(int, input().split())) for __ in range(N)]
    X, Y = map(list, zip(*pos))
    sumX = sum(X)
    sumY = sum(Y)
    answer = inf
    combs = list(combinations(range(N), N // 2))
    for comb in combs[:len(combs) // 2]: # 조합의 절반까지만 살펴보자
        leftX = sumX
        leftY = sumY
        for i in comb:
            leftX -= X[i]
            leftY -= Y[i] # 시작점 기준을 구해준다.
        rightX = sumX - leftX
        rightY = sumY - leftY # 끝점 기준을 구해준다.
        answer = min(answer, ((rightX - leftX) ** 2 + (rightY - leftY) ** 2) ** 0.5)
    print(answer)

여담

이 문제 만든 사람은 시간 제한을 정말 둔 것 같다.
조합 최적화를 해야만 python3가 통과가 되고 아니면 pypy3만 통과가 되게끔 해둔 것 같아서.. ㅎ 쓸데없는 감명이었다.

나도 요즘 문제를 직접 만들어보고 싶다는 생각이 든다.
하지만.. 실력부터 향상해야겠지?

얼른 다음 주에 휴가나 보내고 싶다!!